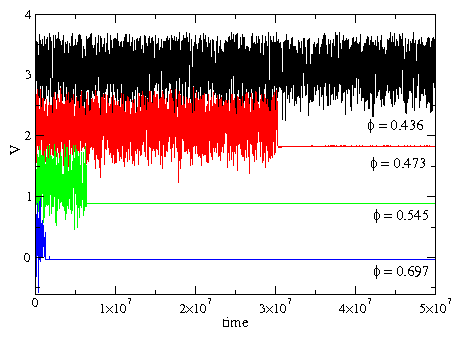
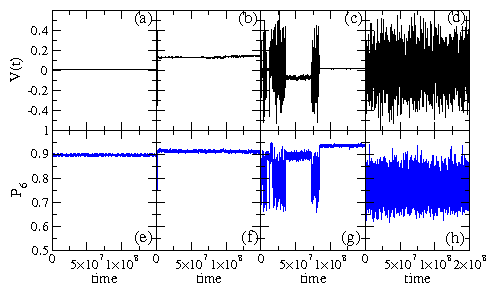
 Fig. 6:
(a,b,c,d) V(t) for a system at ϕ/ϕc = 1.43
where stochastic noise is added in the
form of thermal kicks of magnitude FT = 0 (a), 2.0 (b), 6.0 (c), and
9.0 (d). (e,f,g,h)
The corresponding fraction of particles
with six-fold neighbors P6(t) for a system at
ϕ/ϕc=1.43 and FT = 0 (e), 2.0 (f), 6.0 (g), and 9.0 (h).
Fig. 6:
(a,b,c,d) V(t) for a system at ϕ/ϕc = 1.43
where stochastic noise is added in the
form of thermal kicks of magnitude FT = 0 (a), 2.0 (b), 6.0 (c), and
9.0 (d). (e,f,g,h)
The corresponding fraction of particles
with six-fold neighbors P6(t) for a system at
ϕ/ϕc=1.43 and FT = 0 (e), 2.0 (f), 6.0 (g), and 9.0 (h).
|