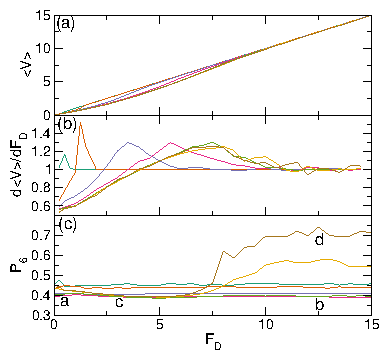
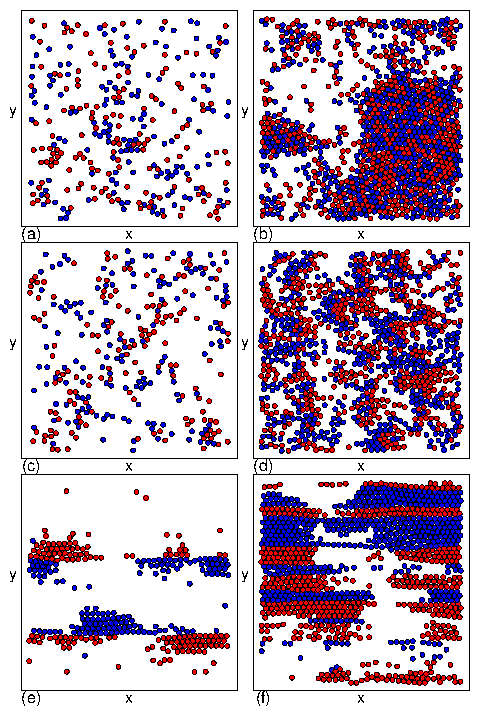
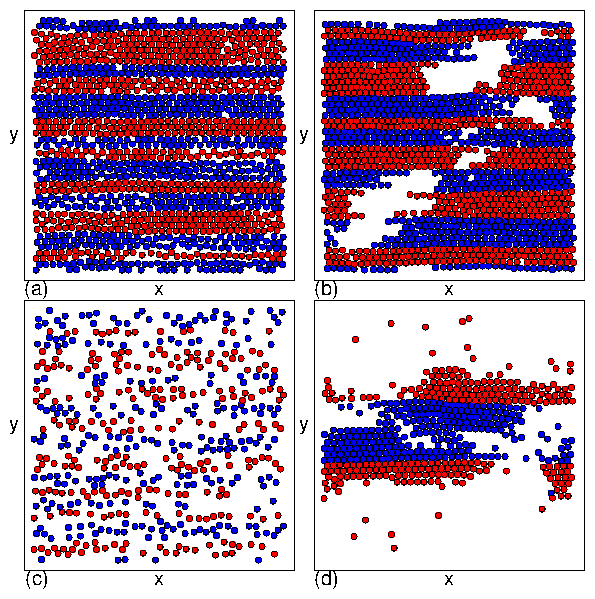
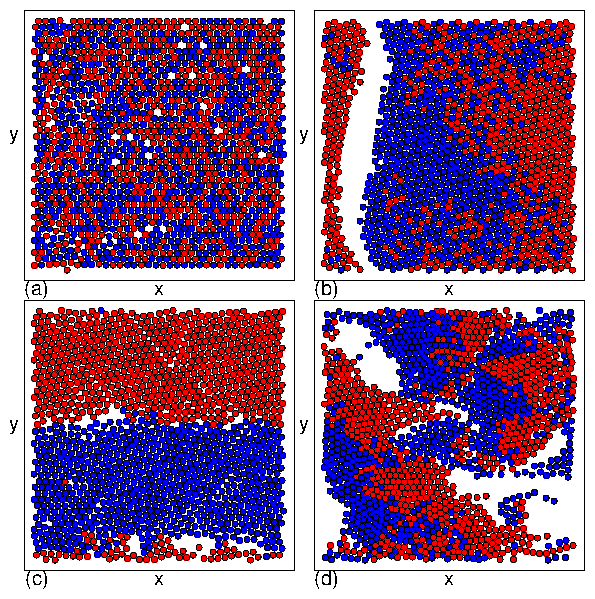
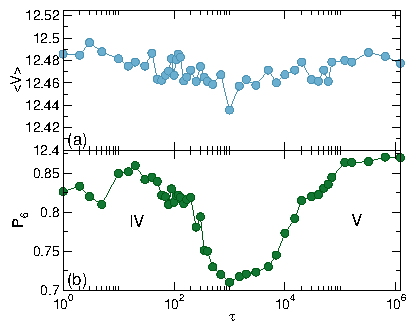
 Figure 11: A system at ϕ = 0.848 with
τ = 10 (dark blue), 150 (light blue), 500 (light green), 2000 (dark green),
and 2 ×104 (gold).
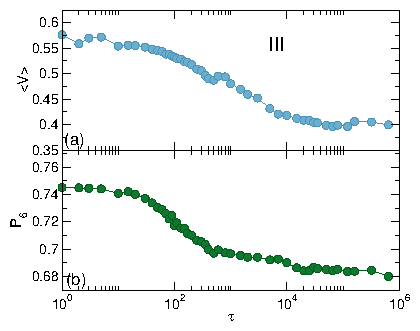
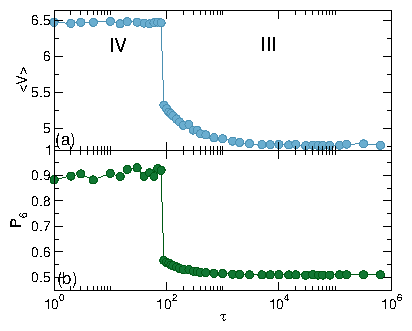
(a) 〈V〉 vs FD.
(b) d〈V〉/dFD vs FD.
(c) P6 vs FD.
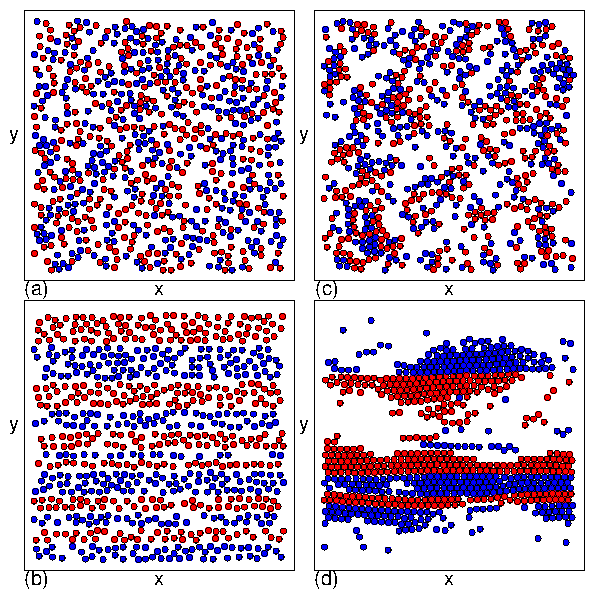
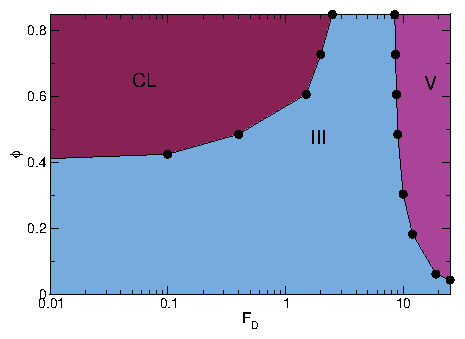
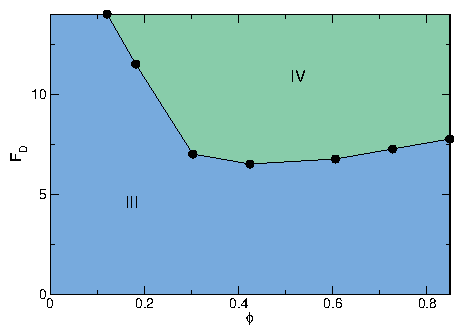
For τ < 500 we observe phase I (jammed), II (phase separated), III (disordered
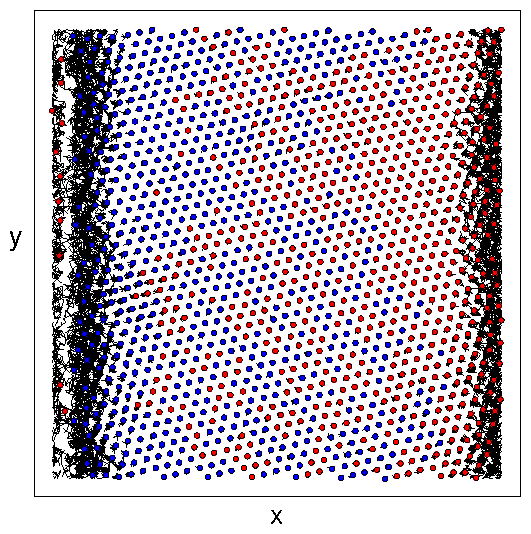
mixed flow), and IV (laning flow).
Transitions between these phases appear as features in
d〈V〉/dFD:
an initial spike near FD=0.15 is the I-II transition,
a negative region near FD=1.0 is the II-III transition, and
the large spike that appears for FD > 5.0 is the III-IV transition.
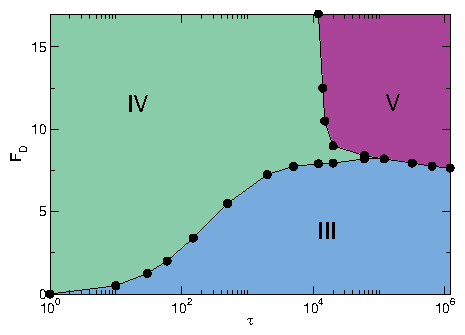
For τ > 1.5 ×104, the III-IV transition
is replaced by a III-V transition.
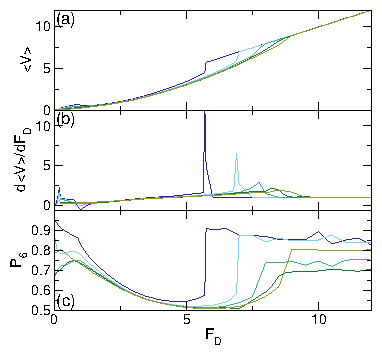
Figure 11: A system at ϕ = 0.848 with
τ = 10 (dark blue), 150 (light blue), 500 (light green), 2000 (dark green),
and 2 ×104 (gold).
(a) 〈V〉 vs FD.
(b) d〈V〉/dFD vs FD.
(c) P6 vs FD.
For τ < 500 we observe phase I (jammed), II (phase separated), III (disordered
mixed flow), and IV (laning flow).
Transitions between these phases appear as features in
d〈V〉/dFD:
an initial spike near FD=0.15 is the I-II transition,
a negative region near FD=1.0 is the II-III transition, and
the large spike that appears for FD > 5.0 is the III-IV transition.
For τ > 1.5 ×104, the III-IV transition
is replaced by a III-V transition.
|