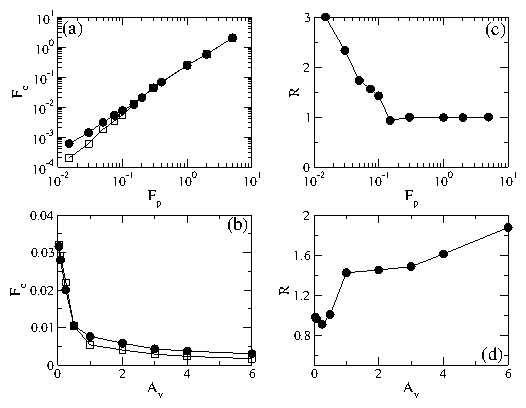
 Figure 7:
(a) The depinning force Fc vs
pinning strength fp for a system with fixed np = 0.66,
n=0.66, rp = 0.3, and NB/N=0.5.
Filled circles: CB/CA = 1.825; open squares: CB/CA = 1.0.
(b) The ratio R of the
bidisperse and monodisperse critical depinning forces from (a).
(c) The depinning force Fc vs
particle interaction strength Z for a system with fixed np = 0.66,
n=0.66, rp = 0.3, and NB/N=0.5.
Filled circles: CB/CA = 1.825;
open squares: CB/CA = 1.0.
(d) The ratio R of the critical depinning forces from (c).
Figure 7:
(a) The depinning force Fc vs
pinning strength fp for a system with fixed np = 0.66,
n=0.66, rp = 0.3, and NB/N=0.5.
Filled circles: CB/CA = 1.825; open squares: CB/CA = 1.0.
(b) The ratio R of the
bidisperse and monodisperse critical depinning forces from (a).
(c) The depinning force Fc vs
particle interaction strength Z for a system with fixed np = 0.66,
n=0.66, rp = 0.3, and NB/N=0.5.
Filled circles: CB/CA = 1.825;
open squares: CB/CA = 1.0.
(d) The ratio R of the critical depinning forces from (c).
|