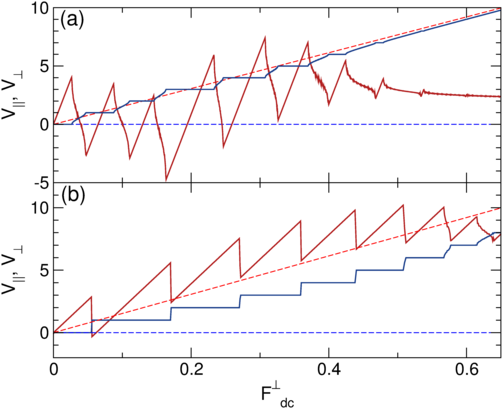
 Figure 3:
(a) V|| (blue) and V⊥ (red) vs F⊥dc for
perpendicular dc driving
and parallel ac driving
at
F||ac = 0.325.
Solid lines: αm/αd=9.96; dashed lines: αm/αd=0.
(b) The same for F||ac = 2.35, where there are
intervals in which V⊥ < 0.
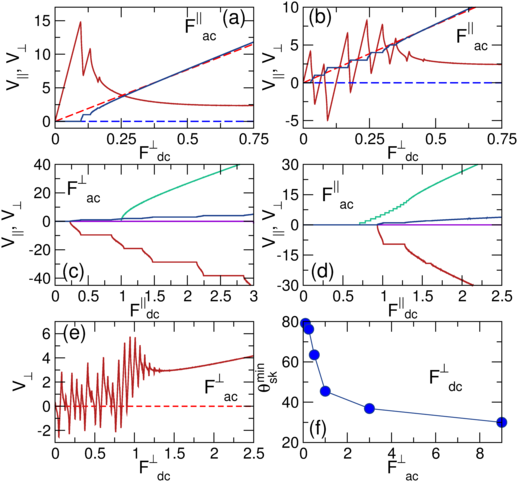
(c) V|| (blue, green) and V⊥ (red, purple) vs F||dc for
parallel dc driving
and
perpendicular ac driving
at
F⊥ac = 0.325
for αm/αd = 9.96 (blue and red), showing Shapiro steps,
and for
αm/αd = 0 (green and purple), where no Shapiro steps occur.
(d) V|| (blue, green) and V⊥ (red, purple) vs F||dc for
parallel dc driving
and parallel ac driving
at F||ac = 0.325
for αm/αd = 9.96 (blue and red)
and αm/αd = 0 (green and purple), showing Shapiro steps.
(e)
V⊥ vs F⊥dc at Ap=1.0 and F⊥ac=1.0 for
αm/αd = 9.96
(solid line) and αm/αd=0 (dashed line)
showing that, compared to Fig. 1(a), there is
an extended region of negative mobility.
(f) The lowest value θskmin
of the
skyrmion Hall angle θsk = tan−1(αm/αd)
for which negative mobility appears
for the system in Fig. 1 as a function of F⊥ac.
For sufficiently large F⊥ac, negative mobility can be observed at
skyrmion Hall angles well below θsk=60°.
Figure 3:
(a) V|| (blue) and V⊥ (red) vs F⊥dc for
perpendicular dc driving
and parallel ac driving
at
F||ac = 0.325.
Solid lines: αm/αd=9.96; dashed lines: αm/αd=0.
(b) The same for F||ac = 2.35, where there are
intervals in which V⊥ < 0.
(c) V|| (blue, green) and V⊥ (red, purple) vs F||dc for
parallel dc driving
and
perpendicular ac driving
at
F⊥ac = 0.325
for αm/αd = 9.96 (blue and red), showing Shapiro steps,
and for
αm/αd = 0 (green and purple), where no Shapiro steps occur.
(d) V|| (blue, green) and V⊥ (red, purple) vs F||dc for
parallel dc driving
and parallel ac driving
at F||ac = 0.325
for αm/αd = 9.96 (blue and red)
and αm/αd = 0 (green and purple), showing Shapiro steps.
(e)
V⊥ vs F⊥dc at Ap=1.0 and F⊥ac=1.0 for
αm/αd = 9.96
(solid line) and αm/αd=0 (dashed line)
showing that, compared to Fig. 1(a), there is
an extended region of negative mobility.
(f) The lowest value θskmin
of the
skyrmion Hall angle θsk = tan−1(αm/αd)
for which negative mobility appears
for the system in Fig. 1 as a function of F⊥ac.
For sufficiently large F⊥ac, negative mobility can be observed at
skyrmion Hall angles well below θsk=60°.
|