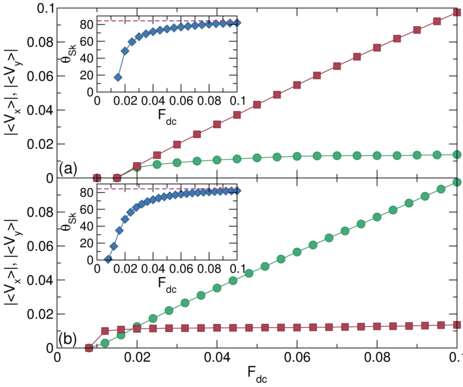
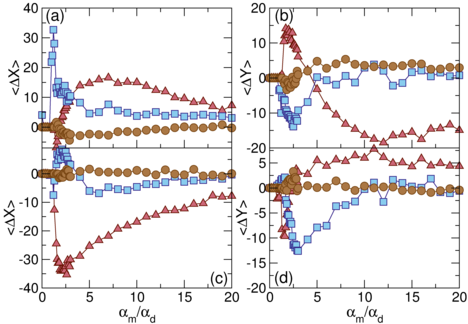
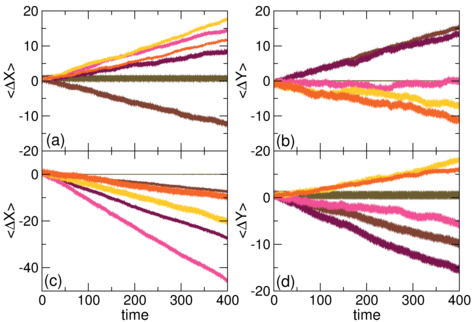
 Figure 4: (a,b) The average cumulative displacement per skyrmion
〈∆X〉 (a) and 〈∆Y〉 (b) vs
time in ac cycles
for the conformal pinning array under longitudinal ac driving
with ns=0.3 and Facx = 0.04 at
αm/αd = 0 (dark green),
1.36 (dark brown),
4.0 (burgundy),
8.0 (dark pink),
10 (yellow),
and 20 (orange).
There is no ratchet motion when αm/αd = 0, but for
αm/αd ≠ 0, we observe ratchet reversals in both the x and y
directions.
(c,d) 〈∆X〉 (c) and 〈∆Y〉 (d) vs time in
ac cycles
for the same system for transverse ac driving
at Facy=0.04 and αm/αd=0
(dark green),
1.2 (dark brown),
1.6 (burgundy),
2.6 (dark pink),
10 (yellow),
and 20 (orange).
In this case the ratchet motion for αm/αd ≠ 0
is always in the negative x direction and shows a reversal in the y direction.
Figure 4: (a,b) The average cumulative displacement per skyrmion
〈∆X〉 (a) and 〈∆Y〉 (b) vs
time in ac cycles
for the conformal pinning array under longitudinal ac driving
with ns=0.3 and Facx = 0.04 at
αm/αd = 0 (dark green),
1.36 (dark brown),
4.0 (burgundy),
8.0 (dark pink),
10 (yellow),
and 20 (orange).
There is no ratchet motion when αm/αd = 0, but for
αm/αd ≠ 0, we observe ratchet reversals in both the x and y
directions.
(c,d) 〈∆X〉 (c) and 〈∆Y〉 (d) vs time in
ac cycles
for the same system for transverse ac driving
at Facy=0.04 and αm/αd=0
(dark green),
1.2 (dark brown),
1.6 (burgundy),
2.6 (dark pink),
10 (yellow),
and 20 (orange).
In this case the ratchet motion for αm/αd ≠ 0
is always in the negative x direction and shows a reversal in the y direction.
|