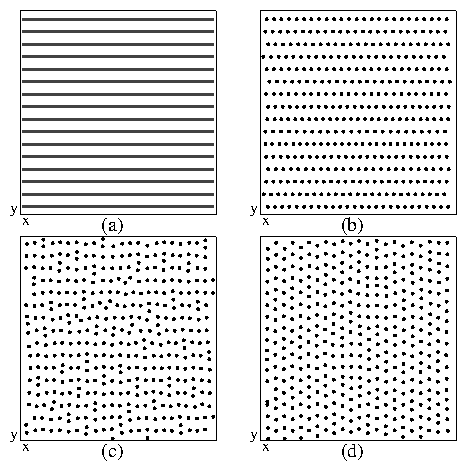
 Figure 1:
(a) Heavy lines: locations of the substrate minima.
(b-d) Black dots: Real space snapshots of the colloid positions
for a system with fixed d, fp=2.0, and nc = 1.35.
(b) Pinned smectic state at fd = 0.
(c) fd/fc = 1.1, where fc is
the depinning threshold. The colloids are moving in the y direction.
(d) fd/fc = 1.2 shows
significant triangular ordering.
Figure 1:
(a) Heavy lines: locations of the substrate minima.
(b-d) Black dots: Real space snapshots of the colloid positions
for a system with fixed d, fp=2.0, and nc = 1.35.
(b) Pinned smectic state at fd = 0.
(c) fd/fc = 1.1, where fc is
the depinning threshold. The colloids are moving in the y direction.
(d) fd/fc = 1.2 shows
significant triangular ordering.
|
