Physical Review B 93, 014504 (2016)

Orientational Ordering, Buckling, and Dynamic Transitions for Vortices Interacting with a Periodic Quasi-One Dimensional Substrate

Q. Thien1,2, D. McDermott1,2, C. J. Olson Reichhardt1, and C. Reichhardt1

1Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Department of Physics, Wabash College, Crawfordsville, Indiana 47933, USA

(Received 21 August 2015; revised manuscript received 11 December 2015; published 7 January 2016)

We examine the statics and dynamics of vortices in the presence of a periodic quasi-one dimensional substrate, focusing on the limit where the vortex lattice constant is smaller than the substrate lattice period. As a function of the substrate strength and filling factor, within the pinned state we observe a series of order-disorder transitions associated with buckling phenomena in which the number of vortex rows that fit between neighboring substrate maxima increases. These transitions coincide with steps in the depinning threshold, jumps in the density of topological defects, and changes in the structure factor. At the buckling transition the vortices are disordered, while between the buckling transitions the vortices form a variety of crystalline and partially ordered states. In the weak substrate limit, the buckling transitions are absent and the vortices form an ordered hexagonal lattice that undergoes changes in its orientation with respect to the substrate as a function of vortex density. At intermediate substrate strength, certain ordered states appear that are correlated with peaks in the depinning force. Under an applied drive the system exhibits a rich variety of distinct dynamical phases, including plastic flow, a density-modulated moving crystal, and moving floating solid phases. We also find a dynamic smectic-to-smectic transition in which the smectic ordering changes from being aligned with the substrate to being aligned with the external drive. The different dynamical phases can be characterized using velocity histograms and the structure factor. We discuss how these results are related to recent experiments on vortex ordering in thin films with periodic thickness modulations. Our results should also be relevant for other types of systems such as ions, colloids, or Wigner crystals interacting with periodic quasi-one-dimensional substrates.
I. INTRODUCTION
II. SIMULATION
III. PINNED PHASES
IV. LATTICE ROTATIONS FOR WEAK SUBSTRATES
V. DYNAMIC PHASES
A. Smectic to smectic transitions
VI. DYNAMICAL PHASE DIAGRAM
VII. DISCUSSION
VIII. SUMMARY
References

I.  INTRODUCTION

Commensurate-incommensurate transitions are relevant to a number of condensed matter systems that can be effectively described as a lattice of particles interacting with an underlying periodic substrate. A commensurate state occurs when certain length scales of the particle lattice match the periodicity of the underlying substrate, such as when the number of particles is equal to the number of substrate minima [1,2]. Typically when commensurate conditions are met, the system forms an ordered state free of topological defects, while at incommensurate fillings there are several possibilities depending on the strength of the substrate. If the substrate potential is weak, the particles maintain their intrinsic lattice structure which floats on top of the substrate, while for strong substrates a portion of the particles lock into a configuration that is commensurate with the substrate while the remaining particles form excitations such as kinks, vacancies, or domain walls. At intermediate substrate strengths, the lattice ordering can be preserved but there can be periodic distortions or rotations of the particle lattice with respect to the substrate lattice [3,4,5,6,7,8]. These different cases are associated with differing dynamical responses of the particles under the application of an external drive [2,7,8,9,10,11]. When kinks or domain walls are present, multi-step depinning process can occur when the kinks become mobile at a lower drive than the commensurate portions of the sample [7,8]. Examples of systems that exhibit commensurate-incommensurate phases include atoms adsorbed on atomic surfaces [1,3,4], vortices in type-II superconductors interacting with artificial pinning arrays [12,13,14,15,16,17,18,19,20,21,22,23,24], vortex states in Josephson-junction arrays [25,26], superfluid vortices in Bose-Einstein condensates in the presence of co-rotating optical trap arrays [27,28,29], cold atoms and ions on ordered substrates [30,31,32,33], and colloidal particles on periodic [6,7,8,34,35,36,37] and quasi-periodic optical substrates [38,39].
In the superconducting vortex system, commensurability occurs when the number of vortices is an integer multiple of the number of pinning sites, and various types of commensurate vortex crystalline states can occur with different symmetries [12,13,16,17,19]. At fillings where there are more vortices than pinning sites, it is possible to have multi-quantized vortices occupy the pinning sites, and a composite vortex lattice can form that is comprised of individual or multiple flux-quanta vortices localized on pinning sites coexisting with vortices located in the interstitial regions between the pinning sites [12,19,20,21,22,23]. Ordered commensurate vortex states have been directly imaged with Lorentz microscopy [13] and other imaging techniques [40,41,42], and the existence of commensurate states can also be deduced from changes in the depinning force needed to move the vortices, with peaks or steps appearing in the critical current as a function of vortex density [12,14,15,16,17,18,19,20,21,22]. It is also possible for ordered vortex structures such as checkerboard states to form at rational fractional ratios of n/m with integer m and n, where n is the number of vortices and m is the number of pinning sites [40,41,42,43,44]. Experiments [7] and simulations [8,45] of colloidal assemblies on optical trap arrays examined the depinning transitions and subsequent sliding of the colloids and show that the depinning threshold is maximum for one-to-one matching of colloids and traps, while it drops at incommensurate fillings due to the presence of highly mobile kinks, anti-kinks, and domain walls.
Commensurate-incommensurate transitions can also occur for particles interacting with a periodic quasi-one-dimensional (q1D) or washboard potential, where the particles can slide freely along one direction of the substrate but not the other. An example of this type of system is shown in Fig. 1 for a two-dimensional system of vortices interacting with a quasi-one dimensional sinusoidal substrate. The potential maxima are indicated by the darker shadings, so the vortices are attracted to the light colored regions. This type of system has been studied previously for colloids interacting with q1D periodic substrate arrays, where it was shown that various melting and structural transitions between hexagonal, smectic, and disordered colloidal arrangements can occur [46,47,48,49,50,51,52]. In general, the colloidal studies focused on the case where the particle lattice constant a is larger than the substrate lattice constant w. Martinoli et al. investigated vortex pinning in samples with a 1D periodic thickness modulation [53,54,55] and observed broad commensuration peaks in the depinning threshold that were argued to be correlated with the formation of ordered vortex arrangements that could align with the substrate periodicity. Other vortex studies in similar samples also revealed peaks in the critical depinning force associated with commensuration effects [56,57], while studies of vortices interacting with 1D magnetic strips showed that commensurate conditions were marked by depinning steps rather than peaks [58]. Under an applied dc drive, depinning transitions occur into a sliding state, and when an additional ac drive is added to the dc drive, a series of Shapiro steps in the voltage-current curves appears when the frequency of the oscillatory motion of the vortex lattice moving over the periodic substrate locks with the ac driving frequency [54]. Similar commensuration effects and Shapiro step phenomena were also studied for vortices interacting with periodic washboard potentials or q1D periodic sawtooth substrates [59]. Vortices interacting with periodic q1D planar defects have also been studied in layered superconductors when the field is aligned parallel to the layer directions. Here, different vortex lattice structures, smectic states, and oscillations in the critical current occur as a function of applied magnetic field [60,61,62,63,64,65,66,67].
Fig1.png
Figure 1: The real space images (left column), with the substrate minima indicated by lighter regions and the vortex positions marked with circles, and the structure factor S(k) (right column), for a system with a periodic quasi-one-dimensional substrate with Fp = 1.5. (a,b) At w/a = 1.85, each substrate minimum contains a single row of vortices (r1) and the structure factor shows smectic order. (c,d) w/a = 2.054, at the onset of a buckling transition. (e,f) At w/a = 2.651 there is an ordered zig-zag r2 vortex lattice. (g,h) At w/a = 3.0 there is a mixture of two and three vortex rows per potential well.
For higher vortex densities in the presence of a q1D substrate where the vortex lattice constant a is smaller than the substrate lattice constant, a < w, there are several possibilities for how the vortices can order. In the weak substrate limit, they can form a hexagonal lattice containing only small distortions, while in the strong substrate limit the vortices could be strongly confined in each potential minima to form 1D rows, so that the overall two-dimensional (2D) vortex structure is anisotropic. Between these limits, the vortices could exhibit buckling transitions by forming zig-zag patterns within individual potential troughs, so that for increasing vortex density there could be a series of transitions at which increasing numbers of rows of vortices appear in the potential troughs. Transitions from 1D rows of particles to zig-zag states or multiple rows have been studied for particles in single q1D trough potentials in the context of vortices [68,69,70], Wigner crystals [71,72,73], colloids [75,75,76,77], q1D dusty plasmas [78,79], ions in q1D traps [80,81,82], and other systems [83,84] where numerous structural transitions, diffusion behavior and dynamics can occur. In the case of a periodic array of channels such as shown in Fig. 1, much less is known about what buckling transitions would occur and what the dynamics would be under an applied driving force. Recently Guillamón et al. studied vortex lattices in samples with a periodic q1D array of grooves. As a function of the commensuration ratio p = w/a, they found that for p < 6, the vortex lattice remains triangular but undergoes a series of transitions that are marked by rotations of the angle θ made by the vortex lattice with respect to the substrate symmetry direction [85]. They also observed that at much higher fields, the system transitions into a disordered state with large vortex density fluctuations. Open questions include what happens to these reorientation transitions as the substrate strength is increased, and what are the vortex dynamics when a driving force is applied. Dynamical phases and structural transitions between different kinds of nonequilibrium vortex flow states have been extensively studied for driven vortex systems interacting with random [86,87,88,89,90,91] and 2D periodic pining arrays [92,93]; however, there is very little work examining the dynamic vortex phases for vortices moving over q1D periodic substrates. It is not known whether the vortices would undergo dynamical structural transitions or exhibit the same types of dynamic phases found for vortices driven over random disorder, such as a disordered plastic flow state that transitions to a moving smectic or anisotropic crystal as a function of increasing drive.
In this work we consider ordering and dynamics of vortices interacting with a periodic q1D sinusoidal potential for fillings 0 < p < 5.5. We study a model representative of vortices in a slab of superconducting material with a q1D surface modulation that is small compared to the slab thickness. In the strong substrate regime, the system undergoes a series of structural transitions that are related to the number of rows of vortices that fit within each substrate trough. These transitions include transformations from 1D vortex rows to zig-zag patterns that gradually increase the number of rows that are confined in a single potential trough. The vortex structure contains numerous dislocations at the buckling transitions and is ordered between the buckling transitions. For strong substrates, the transitions between buckling and ordered phases produce a series of steps in the critical current or depinning force as a function of vortex density, while for weaker substrate strengths, some of the states in which the vortices order produce peaks in the depinning force. For the weakest substrates, the vortices form a triangular lattice that undergoes rotations with respect to the underlying substrate symmetry direction as a function of applied magnetic field, similar to the behavior observed by Guillamon et al. [85]. Under an applied drive we observe plastic flow states, moving density-modulated crystals, and dynamic floating solids. For certain fillings we also find smectic-to-smectic transitions where the two smectic states have different orientations. These different flowing phases produce distinct features in the velocity histograms and the structure factor. The commensurability ratio p also strongly affects the driving force at which the transition to a moving floating solid occurs. Our results should be general to other types of systems that can be represented as a collection of repulsive particles interacting with a periodic q1D substrate, such as colloids on optical line traps, ions in coupled traps, and Wigner crystals on corrugated substrates.

II.  SIMULATION

We model a two-dimensional system of vortices interacting with a periodic q1D potential with period w, where there are periodic boundary conditions in the x and y-directions. The vortices are modeled as point particles and the dynamics of an individual vortex i obeys the following equation of motion:
η d Ri
dt
 = Fivv + Fsi + Fid + FiT.
(1)
Here η is the damping constant which we set equal to unity. The vortex-vortex forces Fvvi = ∑Nvj=1F0K1(Rij/λ)∧Rij, where F0 = ϕ02/2πμ0λ3, ϕ0 is the elementary flux quantum, μ is the permittivity, K1 is the modified Bessel function, Ri is the location of vortex i, Rij = |Ri − Rj|, ∧Rij=(Ri−Rj)/Rij, and λ is the penetration depth. If we match our simulation parameters to the experiment in Ref. [94] on Nb thin films, as an example, we have η = 1.4 ×10−12 N s/m, λ = 368 nm, and F0=1.09 ×10−5 N/m. The vortices have repulsive interactions and form a triangular lattice in the absence of a substrate.
The vortex interaction with the substrate is given by Fsi = −∇V(xi) ∧x where the substrate has the sinusoidal form
V(x) = V0sin(2πx/w).
(2)
We define the pinning strength of the substrate to be Fp = F02πV0/w. Possible ways to experimentally create this type of pinning include growing a uniform thin superconducting film on a wave-modulated substrate or on a flat substrate with periodically modulated interface properties, or growing a superconducting film with periodic thickness modulations. The dc driving force Fid arises from the Lorentz force induced by a current applied along the easy direction (y-axis) of the substrate which produces a perpendicular force on the vortices and causes them to move in the x-direction in our system. Our simulations are performed in the limit that is well below the Larkin-Ovchinnikov instability where vortex cores may deform [95]. We measure the vortex velocity 〈Vx〉 along the driving direction as we increase the external drive in increments of δFd, and average the vortex velocities over a fixed time in order to avoid any transient effects. The thermal forces FT are modeled as random Langevin kicks with the properties 〈FT〉 = 0 and 〈FiT(t)FTj(t′)〉 = 2ηkBTδijδ(t − t′), where kB is the Boltzmann constant. The initial vortex positions are obtained by annealing from a high temperature state and cooling down to T = 0. The dc drive is applied only after the annealing procedure is completed. We consider a range of vortex densities, which we report in terms of the ratio w/a of the periodicity of the substrate to the vortex lattice constant that would appear in the absence of a substrate. We denote a state containing n rows of vortices in each potential minimum as rn.

III.  PINNED PHASES

In Fig. 1(a,c,e,g), we plot the real space locations of the vortices on the potential substrate after annealing for a system with Fp = 1.5 at fillings of w/a = 1.85, 2.054, 2.651, and 3.0, while in Fig. 1(b,d,f,h) we show the corresponding structure factors S(k). At w/a = 1.58 in Fig. 1(a) the vortices form single 1D rows in each potential minimum, corresponding to an r1 state, and the overall vortex structure is highly anisotropic with lattice constants ax = 4.5 in the x−direction and ay = 1.31 in the y−direction. Additionally, each potential trough captures a slightly different number of vortices, introducing disorder in the alignment of rows in adjacent minima, and leaving the system with periodic ordering only along the x-direction. The corresponding structure factor in Fig. 1(b) exhibits a series of spots at ky = 0.0 and finite kx, indicative of the 1D ordering associated with a smectic phase. As the magnetic field increases, the vortex ordering must become increasingly anisotropic in order to maintain single rows of particles in each minimum. This is energetically unfavorable, so instead a transition occurs to a zig-zag or buckled state in which there are two partial rows of vortices in every substrate minimum. Figure 1(c) illustrates the real space vortex positions for w/a = 2.054 at the beginning of the zig-zag transition, where some of the troughs contain a buckled vortex pattern. In the corresponding S(k) plot in Fig. 1(d), the smectic ordering develops additional features at large k associated with the shorter range structure that arises on the length scale associated with the zig-zag pattern. As the magnetic field is further increased, the zig-zag pattern appears in all the substrate minima and the system forms an ordered anisotropic 2D r2 lattice as shown in Fig. 1(e) for w/a = 2.651, where there are two rows of vortices in each potential minimum that form a zig-zag structure which is aligned with zig-zag structures in neighboring minima. The corresponding S(k) in Fig. 1(f) has a series of peaks at small and large k indicating the presence of a more ordered vortex structure. For higher fields, the zig-zag lattice becomes increasingly anisotropic until another buckling transition occurs to produce r3 with three vortex rows per substrate minimum. Figure 1(g) shows the transition point at w/a = 3.0 where certain potential troughs contain three vortex rows while others contain two vortex rows or mixtures of two and three vortex rows. In Fig. 1(h), S(k) for this case shows that the system is considerably more disordered than at the commensurate case illustrated in Fig. 1(e,f).
Fig2.png
Figure 2: The continuation of the real space images (left column) and S(k) (right column) from the system in Fig. 1 with Fp=1.5. (a,b) At w/a = 3.3, there is an ordered structure with three vortex rows per potential minimum (r3). (c,d) At w/a = 3.644, there is a partially disordered state with roughly three vortex rows per potential minimum. (e,f) At w/a = 4.1455 there is a partially ordered state with four vortex rows per minimum (r4). (g,h) The disordered state at w/a = 5.15 showing ring structures in S(k).
In Fig. 2 we show the continuation of the evolution of the vortex lattice from Fig. 1 in both real space and k-space. At w/a=3.3 in Fig. 2(a), there is an ordered r3 structure with three vortex rows in each potential minimum, producing the ordered S(k) shown in Fig. 2(b). As the vortex density is further increased, the row structure disorders as shown in Fig. 2(c) for w/a = 3.644, corresponding to a ring like structure in S(k) as indicated in Fig. 2(d). There are still peaks along the ky = 0.0 line due to the anisotropy induced by the substrate. For this value of Fp, further increasing the vortex density does not produce a more ordered configuration; however, certain partially ordered structures can occur as illustrated in Fig. 2(e) for w/a = 4.1455, where there are four vortex rows per trough (r4) with mixed peaks and smearing in the corresponding structure factor shown in Fig. 2(f). At higher fields, the vortex structures become disordered as shown in Fig. 2(g) at w/a = 5.15, where S(k) in Fig. 2(h) has pronounced ring structures. There are still two peaks at ky=0 and finite kx due to the smectic ordering imposed by the q1D substrate.
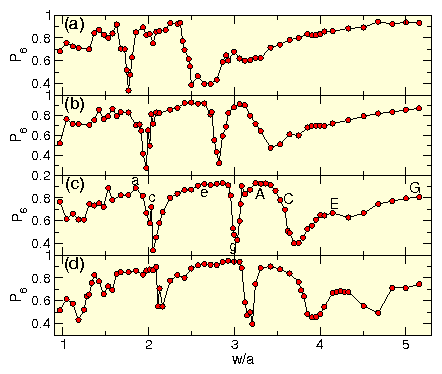
Fig3.png
Figure 3: The fraction of six-fold coordinated vortices P6 vs w/a for (a) Fp = 0.5, (b) Fp = 1.0, (c) Fp = 1.5 and (d) Fp = 2.0. In panel (c), the labels a, c, e, g indicate the values of w/a at which the images in Fig. 1 were obtained, while the labels A, C, E, and G indicate the values of w/a at which the images in Fig. 2 were obtained. The dips in P6 coincide with transitions in the number of vortex rows contained within each potential minimum.
We can also characterize the system using the fraction of six-fold coordinated vortices P6=N−1∑i=1Nδ(6−zi), where zi is the coordination number of vortex i obtained from a Voronoi construction. In general, we find that P6 drops at the buckling transitions due to the formation of dislocations that are associated with the splitting of a single row of vortices into two rows, creating a kink at the intersection of the two rows. In Fig. 3(a) we plot P6 versus w/a for a system with Fp = 0.5. Over the range 1.0 < w/a < 1.7, each pinning trough contains an r1 state, while the dip in P6 at w/a = 1.77 corresponds to the middle of the buckling transition when there is roughly a 50:50 mixture of r1 and r2. For 1.85 < w/a < 2.35, the system forms an ordered r2 state similar to that shown in Fig. 1(e), but less anisotropic since the weaker substrate compresses the zig-zag structure less and permits it to be wider. Near w/a = 2.4, there is another buckling transition from r2 to r3 and the system forms a disordered state similar to that shown in Fig. 1(g). As w/a is further increased, there is a partially ordered state near w/a = 3 that is similar to the state in Fig. 2(a); however, due to the weaker substrate strength a fully ordered r3 state does not form. For w/a > 3.2 the system adopts a polycrystalline configuration that becomes more ordered at high vortex densities. In Fig. 3(b), we show that a similar set of features associated with buckling transitions occurs for a stronger substrate with Fp = 1.0; however, in this case the transition from r2 to r3 is sharper and a fully ordered three row state appears near w/a = 3.0.
In Fig. 3(c) we plot P6 versus w/a for samples with Fp = 1.5, the same pinning strength at which the images in Figs. 1 and 2 were obtained. Here the dips in P6 associated with the r1 to r2, r2 to r3, and r3 to r4 transitions are sharper. We also observe the development of a small dip near w/a = 4.4 corresponding to a partial transition from r4 to r5. The values of w/a at which row transitions occur shift upward with increasing Fp. For example, the r1 to r2 transition occurs at w/a=1.768 for Fp=0.5 but at w/a=2.05 for Fp=1.5, since the higher Fp stabilizes the r1 state up to higher anisotropies. Figure 3(d) shows P6 versus w/a for samples with Fp = 2.0. Here the dip in P6 at the r1 to r2 transition broadens, while a pronounced jump emerges at w/a = 4.7 corresponding to the r4 to r5 transition. We expect that for higher values of Fp, additional dips in P6 for transitions from rn to rn+1 states for n ≥ 5 will appear at w/a values higher than those we consider here.
It is difficult to determine if the buckling transitions are first or second order in nature. For particles in an isolated trough, the transition from a single row to a zig-zag pattern is second order, and there have been several studies in cold ion systems of quenches through this transition in which the density of kinks was calculated for different quench rates and compared to predictions from nonequilibrium physics on quenches through continuous phase transitions [80,81,82]. We expect that the buckling transitions we observe are second order; however, it may be possible that the additional coupling to particles in neighboring potential minima could change the nature of the transition, and we have observed a coexistence of chain states which is suggestive of phase separation. For vortex systems it could be difficult to change the substrate strength as a function of time, but for colloidal systems it is possible to create q1D periodic optical substrates of adjustable depth and use them to study time dependent transitions by counting the number of kinks that form as a function of the rate at which the substrate strength is changed.
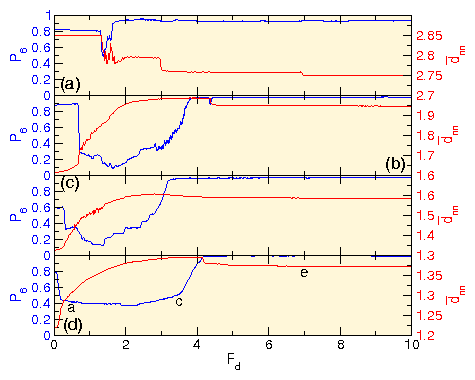
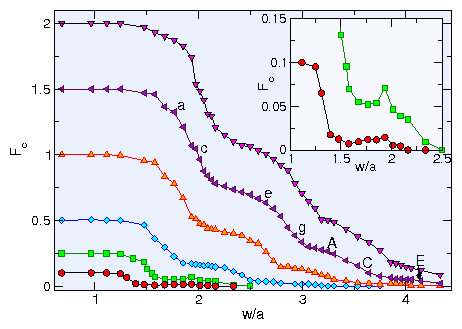
Fig4.png
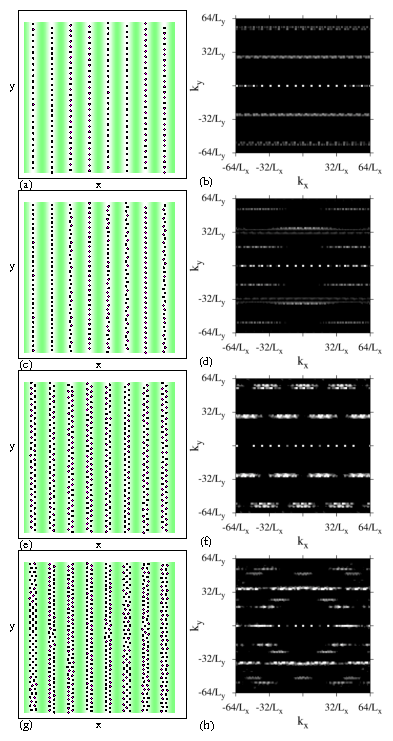
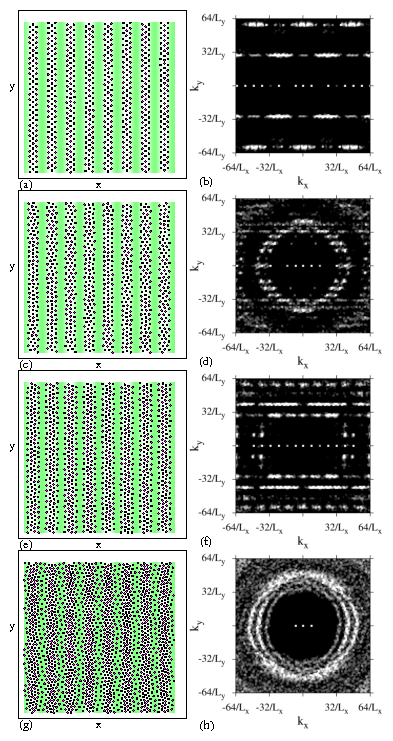
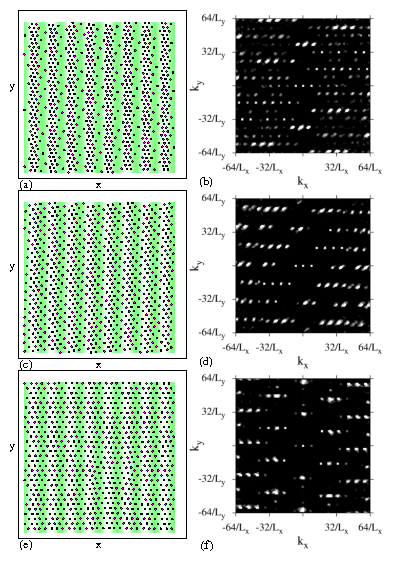
Figure 4: The depinning force Fc vs w/a for Fp = 0.1 (circles), 0.25 (squares), 0.5 (diamonds), 1.0 (up triangles), 1.5 (left triangles), and 2.0 (down triangles) showing that for Fp > 0.25 the buckling transitions correspond to step features in Fc. The labels a, c, e, g indicate the values of w/a at which the images in Fig. 1 were obtained, while the labels A, C, and E indicate the values of w/a at which the images in Fig. 2 were obtained. Inset: a highlight of the main panel illustrates that for weaker pinning, peaks in Fc occur, as shown for Fp=0.1 (circles) and 0.25 (squares). 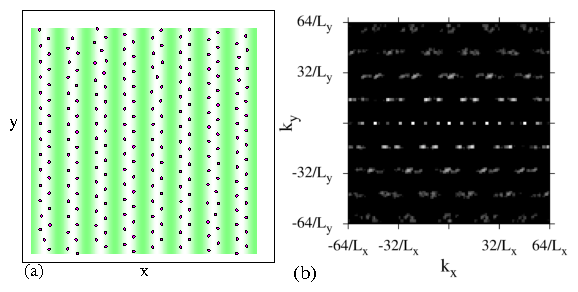The peak is associated with the formation of an ordered zig-zag lattice similar to that shown in Fig. 1(e).
Fig5.png
Figure 5: (a) Real space image of the vortex configuration at the peak in Fc at Fp = 0.5 and w/a = 1.94 for the system shown in the inset of Fig. 4 where an ordered zig-zag structure occurs. (b) The corresponding S(k) contains various peaks reflecting the ordered nature of the state.
In Fig. 4 we plot the depinning force Fc versus w/a for Fp = 0.1, 0.25, 0.5, 1.0, 1.5, and 2.0 to show that the buckling transitions are associated with changes in the slope of the depinning force, which decreases with increasing w/a in a series of steps. The first drop in Fc near w/a = 2.0 corresponds to the r1 to r2 transition. In the r1 state, the particle-particle interactions roughly cancel in the x-direction, so the depinning force is approximately equal to Fp, while close to the buckling transition the vortices on the right side of a zig-zag experience an additional repulsive force in the driving direction from the vortices on the left side of the zig-zag, decreasing the driving force needed to depin the vortices. To estimate the magnitude of this reduction in Fc, we note that the average x-direction spacing between vortices in a given zig-zag is approximately rx=2.0. For a zig-zag with a 30° angle between the two closest neighbors on the other side of the chain from each vortex, the vortex-vortex interaction force of K1(2) produces an additional repulsive force of fr=0.55, giving a value of Fc=Fp−fr that is close to the value of Fc=0.78 observed after the r1 to r2 step for the Fp=1.5 system. Similar arguments can be made for the magnitudes of the drops in Fc at the higher order transitions as well. At w/a = 1.85 in the Fp=1.5 sample, Fc already begins to drop below Fp even though the pinned configuration shown in Fig. 1(a) is an r1 state. This occurs because in this range of w/a, application of a finite Fd < Fc induces a slight buckling of the vortices, while for w/a < 1.5 the r1 rows remain in a 1D pinned state up to Fd = Fc. The inset of Fig. 4 shows a blowup of Fc versus w/a for the weaker pinning cases Fp = 0.25 and Fp=0.1. At w/a=1.94 there is a peak in Fc for the Fp=0.25 sample coinciding with the formation of the long range ordered zig-zag state shown in Fig. 5(a). The corresponding S(k) in Fig. 5(b) contains a series of peaks that reflect the ordered nature of the state, which resembles the zig-zag state in Fig. 1(e,f) expect that the system is more ordered and the zig-zag structure is wider. For Fp = 0.1 the zig-zag state transitions into a hexagonal lattice and the peak in Fc begins to disappear. Some experiments examining vortices in q1D periodic pinning structures show that peaks in the critical current occur at certain fillings [53,55,56,57] in regimes where the pinning is weak, whereas other experiments performed in the strong pinning limit reveal more step-like features in the critical current. This suggests that the experiments in the strong pinning limit are producing buckling transitions [58].
Fig6.png
Figure 6: Real space images (left column), with the substrate minima indicated by lighter regions and the vortex positions marked with circles, and S(k) (right column). (a,b) At Fp = 0.5 and w/a = 4.825 there is a polycrystalline structure. (c,d) At Fp = 2.0 and w/a = 4.33 there is a partially ordered r4 structure. (e,f) At Fp = 2.0 and w/a = 4.67, an ordered structure appears. (g,h) At Fp = 2.0 and w/a = 5.15 the structure is disordered.
In Fig. 6 we plot representative real space images with the matching S(k) for some other substrate strengths to highlight other types of ordering we observe. Figure 6(a) shows the real space ordering of the vortices at Fp = 0.5 and w/a = 4.825, where the vortex lattice is polycrystalline and contains regions of triangular ordering with different orientations. The corresponding structure factor in Fig. 6(b) has ring features with some remnant of the smectic ordering appearing at smaller values of k. In Fig. 6(c), at Fp = 2.0 and w/a = 4.33 an r4 state appears, while S(k) in Fig. 6(d) has smectic ordering features along with additional crystalline ordering signatures due to the ordered arrangement of the particles within the troughs. At Fp = 2.0 and w/a = 4.67 in Fig. 6(e) a new type of ordered structure appears in which the vortices can pack more closely by forming alternate regions of r3 and r4 states, producing a considerable amount of triangular ordering as seen in the plot of S(k) in Fig. 6(f), where there are sixfold peaks at large k and smectic peaks at smaller k. In Figs. 6(g,h), for Fp = 2.0 and w/a = 5.15, a more disordered structure appears, with some regions of the sample containing r4 or r5 states.

IV.  LATTICE ROTATIONS FOR WEAK SUBSTRATES

Fig7.png
Figure 7: Real space images of the vortices in a sample with Fp = 0.2 showing that the hexagonal vortex lattice can adopt various orientations θ with respect to the substrate periodicity direction. (a) At w/a = 2.0, θ = 2.4°. (b) At w/a = 3.272, θ = 24°. (c) At w/a = 3.53, θ = 27.1°. (d) At w/a = 3.75, θ = 13.2°.
We have also studied systems with a pinning strength of Fp = 0.02. Here, for w/a > 1.77 the vortices form a triangular lattice and the features associated with the buckling transitions observed in Fig. 3 are lost. In this case the vortex lattice can orient at various angles with respect to the underlying substrate. We measure this angle as in Ref.[85] by identifying the smallest positive angle between a major symmetry axis of the vortex lattice and the x axis, which is the underlying substrate periodicity direction. In Fig. 7(a) we show the real space vortex positions at w/a = 2.8, where the vortices form a triangular lattice that is aligned at an angle θ = 2.4° with respect to the x-axis. In Fig. 7(b) at w/a = 3.272, θ = 24°, while in Fig. 7(c) at w/a = 3.53, θ = 27.1°, and in Fig. 7(d) at w/a = 3.75, θ = 13.2°. In Ref. [85], Guillamon et al. observed experimentally that vortices on a q1D substrate retained triangular ordering but that the vortex lattice was oriented at an angle θ ranging from θ = 0 to θ = 30° with respect to the substrate. In several cases, they found that the system locked to specific angles close to θ = 30°, θ = 24°, and θ = 0°. We find a much larger variation in the orientation of the lattice with respect to the substrate as a function of filling than was observed in the experiments, which may be due to differences the pinning strength or the finite size of our simulations. Our results show that for weak pinning, the buckling transitions are lost and are replaced with orientational transitions of the vortex lattice with respect to the substrate. Another feature we observe when the pinning strength is increased is that the vortex lattice becomes disordered or polycrystalline. Guillamon et al. also observe that at higher fillings the vortex lattice becomes disordered; however, in their system there are strong random vortex density fluctuations, while for our samples the vortex density at higher fields is generally uniform.

V.  DYNAMIC PHASES

Fig8.png
Figure 8: The fraction of six-fold coordinated vortices P6 (dark black curves) and the average nearest-neighbor distance ―dnn (light red curves) vs Fd for a system with Fp = 1.5. (a) At w/a = 1.767 the system depins from an r1 state. (b) At w/a = 2.5 the system dynamically orders into a moving triangular lattice with P6 = 0.97. (c) w/a = 3.061. (d) At w/a = 3.535, the onset of the dynamically ordered phase coincides with a drop in ―dnn near Fd = 4.0. The labels a, c, and e correspond to the values of Fd used for the images in Fig. 9.
In Fig. 8 we plot simultaneously P6 and the average nearest neighbor spacing ―dnn versus Fd for a sample with Fp = 1.5 at varied w/a. Here, we obtain ―dnn by performing a Voronoi tessellation to identify the zi nearest neighbors of particle i, and then take ―dnn=(N ∑i zi)−1∑i=1N∑j=1zirij, where rij is the distance between particle i and its jth nearest neighbor. For w/a = 1.76 in Fig. 8(a), P6=0.83 in the pinned r1 state that occurs for 0 < Fd < 1.4. There is a dip in P6 over the range 1.4 < Fd < 1.7, corresponding to the plastic flow state in which some of the vortices remain immobile while other vortices hop in and out of the potential wells. For Fd > 1.7, P6 increases and reaches a saturated value of P6=0.93 when the vortices form a moving triangular lattice containing a small fraction of dislocations. The value of ―dnn drops at the depinning transition, and several additional drops in ―dnn occur at higher drives. In the r1 pinned state, each vortex has two close nearest neighbors that are in the same pinning trough, and four more distant nearest neighbors that are in adjacent pinning troughs. Once the vortices depin and enter a moving state, they adopt a more isotropic structure, causing ―dnn to drop as the distance to the four more distant nearest neighbors decreases. The additional drops in ―dnn at higher Fd occur whenever the vortex lattice rearranges to become still more isotropic.
In Fig. 8(b) we plot P6 and ―dnn versus Fd for the same sample at w/a = 2.5 where an ordered zig-zag state with P6=0.89 appears at zero drive, as shown in Fig. 1(e). The depinning threshold is Fc = 0.65, much lower than the value of Fc for the w/a=1.767 filling in Fig. 8(a), and the depinning transition is marked by a drop in P6 to P6=0.2. Over the range 0.65 < Fd <~2.0, the vortices are in a dynamically disordered state, while the saturation of ―dnn above Fd ≈ 2.0 indicates that a partially ordered state has formed. The value of P6 does not reach a maximum until Fd = 3.9, where P6 ≈ 0.97 and an ordered state appears. For 1.5 < Fd < 3.9, we observe a moving density-modulated solid. The value of Ftrc, the drive at which the sample reaches a moving triangular lattice state, is higher for w/a=2.5 than for w/a=1.767, even though the depinning threshold Fc is smaller for the w/a=2.5 system. At w/a=2.5, ―dnn is initially small and jumps up at the depinning transition, unlike the decrease in ―dnn at depinning found in Fig 8(a). Since the vortices in Fig. 8(b) form a zig-zag r2 structure in the pinned state, each vortex has four close nearest neighbors in the same pinning trough, and two more distant nearest neighbors in an adjacent pinning trough. This causes ―dnn to be smaller in the pinned state than it was for the r1 structure in Fig. 8(a), and when the vortex lattice becomes more isotropic in the moving state, ―dnn increases rather than decreasing as the two halves of each zig-zag structure move further apart. At Fd = 4.1 we observe a drop in ―dnn that coincides with a dip in P6. This feature is associated with a transition from a density-modulated lattice to a more uniform moving floating lattice.
In Fig. 8(c), we show P6 and ―dnn versus Fd at w/a = 3.06 where there is an r3 pinned state, as illustrated in Fig. 2(a). Here the depinning threshold Fc = 0.3, and the system transitions into a moving triangular lattice at Ftrc = 1.6, which is somewhat lower than the value of Ftrc for w/a = 2.5 in Fig. 8(b). The behavior of ―dnn in Fig. 8(c) follows a similar pattern as in Fig. 8(b), with ―dnn increasing with increasing Fd. We plot the same quantities for w/a=3.53 in Fig. 8(d), where the depinning threshold Fc ≈ 0.087 and the system dynamically orders for Fd > 4.0. There is a small dip in ―dnn at Fd = 4.15 along with a saturation in P6 which is correlated with a structural change to a dynamic floating lattice.
Fig9.png
Figure 9: Real space images (left column), with the substrate minima indicated by lighter regions and the vortex positions marked with circles, and S(k) (right column) for the dynamic system from Fig. 8(d) with Fp=1.5 and w/a=3.535 at the values of Fd labeled a, c, and e. (a,b) At Fd = 0.5 the sample contains pinned vortices coexisting with individual vortices that hop from trough to trough. (c,d) At Fd = 3.5, all the vortices move together to form a disordered lattice with a periodic density modulations. (e,f) At Fd = 7.0 the system forms a moving floating triangular lattice.
In order to characterize the nature of the dynamic vortex structures in the moving states, in Fig. 9(a,b) we plot the real space images and S(k) for the system in Fig. 8(d) at w/a = 3.53 and Fd = 0.5. Here, individual vortices jump from one pinning well to the next while a portion of the vortices remain immobile in the substrate minima. As shown in the plot of S(k), the vortex configuration is fairly ordered and takes the form of a distorted non-triangular structure which causes P6 to be low for this value of Fd. For Fd > Fp, the vortices move together so there is no plastic motion, and form a distorted lattice containing pronounced density modulations as shown in Fig. 9(c,d) for Fd = 3.5. For Fd > 4.0 we find a transition from the density modulated lattice to a moving homogeneous floating triangular lattice which coincides with the drop in ―dnn in Fig. 8(d) and the maximum in P6. Fig. 9(e) shows the floating lattice at Fd = 7.0, where as illustrated in Fig. 9(f) S(k) contains sixfold peaks that are indicative of triangular ordering. The smectic ordering induced by the substrate is substantially weaker or almost absent at this drive, as shown by the weakness of the spots in S(k) at ky = 0, indicating that the system has formed a floating solid. We find similar types of transitions in the dynamics at other fillings as well.
Fig10.png
Figure 10: Vortex velocities for the system in Fig. 9 with Fp = 1.5 and w/a = 3.535. Left column: Histogram P(Vx) of the instantaneous vortex velocities in the driving direction Vx. Center column: Histogram P(Vy) of the instantaneous vortex velocities in the transverse direction Vy. Right column: Heightfield map of Vy versus Vx. (a,b,c) The plastic flow regime at Fd = 0.5. (d,e,f) The moving modulated solid regime at Fd = 3.5. (g,h,i) The moving floating solid regime at Fd = 7.0.
We can also characterize the different dynamic states in Figs. 8 and 9 by examining histograms of the vortex velocities. In Fig. 10(a) we plot the distribution P(Vx) of Vx in the driving direction at Fd = 0.5 for the system in Fig. 8(a,b) with Fp = 1.5 and w/a = 3.535. Figure 10(b) shows the transverse velocities P(Vy), while in Fig. 10(c) we plot Vy versus Vx as a heightfield map. At this drive, the motion is plastic and occurs by individual vortex hopping, so there is a sharp peak in P(Vx) at Vx=0.15 which reflects the fact that most of the vortices are slowly moving within an individual pinning trough. When a single vortex jumps into an adjacent pinning trough, it creates a pulse of motion through the trapped vortices that triggers the jump of another single vortex to the next pinning trough, where the process repeats. This depinning cycle creates two peaks in P(Vx). The peak at low Vx corresponds to the motion of a velocity pulse through the dense assembly of vortices at the bottom of the pinning trough, while the peak at high Vx is produced by individual vortices escaping over the potential maximum. This peak falls near Vx=1.1, which is larger than Fd, reflecting the fact that after an individual vortex passes the crest of the substrate maximum, the substrate contributes an additional force term in the driving direction as the vortex moves toward the next substrate minimum. In this case the maximum force exerted by the pinning site is Fp=1.5 while the driving force is Fd=0.5, so that the maximum possible instantaneous vortex velocity would be Vx=2.0; however, vortex-vortex interactions prevent individual vortices from moving this rapidly. In Fig. 10(b), P(Vy) is centered at Vy=0 since there is no driving force in the transverse direction; however, we observe some asymmetry in P(Vy) as well as peaks at finite Vy due to the fact that the vortex lattice segments inside the pinning troughs are oriented at an angle with respect to the substrate symmetry direction, as shown in Fig. 9(a). This asymmetry also appears in the Vy versus Vx plot in Fig. 10(c), which has two prominent features. The first is a wide band of Vy values at low Vx that are associated with soliton-like pulses moving through the dense regions of the vortex clusters, which pushes vortices in both the positive and negative y-direction.
In Fig. 10(d,e,f) we show instantaneous velocity plots for the system in Fig. 9(c,d) with Fd = 3.5 where the vortices are moving elastically in the density-modulated solid phase. Here P(Vx) in Fig. 10(d) has peaks at Vx=2.01 and Vx=4.75 which are smoothly connected by finite P(Vx) values. The shape of this histogram shows the velocity imposed by the driving force of Fd = 3.5 when the substrate forces alternately act with or against the driving force. When the substrate force is against the drive the velocity is Vx=Fd − Fp = 2.0, while when the substrate and driving forces are in the same direction, Vx=Fd + Fp = 5.0, close to the observed values of the peaks in P(Vx). In Fig. 10(e), P(Vy) has two peaks close to Vy=0.1 and Vy=−0.1, indicating that there is an oscillatory motion in the y-direction. This effect can be seen more clearly in the Vy versus Vx plot in Fig. 10(f) which has two symmetric lobes. Since the vortices are in a density-modulated lattice, shearing in the y-direction occurs between adjacent density modulations, with one density modulation moving in the positive y-direction while the other moves in the negative y-direction.
The velocity plots for the system in Fig. 9(e,f) at Fd = 8.5 appear in Fig. 10(g,h,i). In Fig. 10(g), P(Vx) has a two-peak feature similar to that in Fig. 10(d), but with peak values at Vx=7.0 and Vx=10. Figure  10(h) shows that P(Vy) has a single peak centered at Vy = 0, while in Fig. 10(i), there is a single lobe in the Vy versus Vx plot. Here the vortices have formed a floating triangular solid, and their motion is close to one-dimensional along the driving direction. As Fd is further increased, the width of the lobe feature gradually decreases. We find similar histograms for the other fillings in the strong pinning limit for the plastic flow, moving modulated solid, and moving floating solid regimes.

A.  Smectic to smectic transitions

Fig11.png
Figure 11: Real space images (left column), with the substrate minima indicated by lighter regions and the vortex positions marked with circles, and S(k) (right column) for a system at Fp = 0.5 and w/a = 1.767. (a,b) The plastic flow phase at Fd = 0.3 where there is individual vortex hopping form well to well and S(k) indicates a smectic phase with periodic ordering along the x−direction. (c,d) At Fd = 0.6, all the vortices are flowing and form chains that are aligned in the x-direction. S(k) shows that a new smectic order has appeared with periodic ordering along the y-direction. (e,f) At Fd = 3.6 there is a moving floating triangular crystal.
Fig12.png
Figure 12: Vortex velocities for the system in Fig. 11. Left column: P(Vx). Center column: P(Vy). Right column: Heightfield map of Vy versus Vx. (a,b,c) The plastic flow phase at Fd = 0.3 where there is a large peak in P(Vx) at Vx = 0 due to the pinned vortices. (d,e,f) The moving smectic phase from Fig. 11(c,d) at Fd = 0.6. (g,h,i) The moving triangular solid phase at Fd = 3.6.
For Fp < 1.0, we find that a dynamically induced smectic to smectic transition can occur. In Fig. 11(a,b) we show the real space and S(k) images for a system with Fp = 0.5 and w/a = 1.767 in the plastic flow regime where there is a combination of vortices that are trapped in the pinning troughs and a smaller amount of vortices that hop by jumping from one trough to the next and then triggering a jump of another vortex from one trough to the next. Here, S(k) indicates that the overall system has smectic ordering due to the chain-like structure of the vortices within the pinning troughs. In Fig. 12(a) we plot P(Vx) at Fd = 0.3, where there is a peak at Vx=0 due to the pinned vortices along with a small bump at Vx = 0.6 due to the vortex hopping. Figure 12(b) shows that P(Vy) has a maximum at Vy = 0, while in Fig. 12(c), the Vy versus Vx plot is asymmetric in Vy, with a peak at Vx = Vy = 0.0 and a second peak at higher Vx produced by the moving vortices.
In Fig. 11(c) we show the real space vortex configuration at Fd = 0.6, which is higher than the maximum pinning force of Fp = 0.6. All the vortices are in motion, but instead of retaining their alignment along the y-direction induced by the substrate, they form a chain-like structure aligned in the x-direction with a slight tilt in the positive y-direction. This alignment in the drive direction is more clearly seen in the corresponding S(k) in Fig. 11(d), where the peaks fall along kx = 0.0, indicating a smectic phase with ordering along the y-direction. There are some very weak peaks on the ky = 0.0 axis due to the substrate, but overall the vortex structure is a smectic state rotated 90° from the y-axis. The strongest S(k) peaks do not fall exactly at kx = 0 but are at a slight angle, due to the channels in Fig. 11(c) being slightly tilted in the positive y-direction. In Fig. 12(d), the corresponding P(Vx) shows a peak at Vx = 0.19, while there is an absence of weight in P(Vx) at Vx = 0.0, indicating that the vortices are always in motion. Figure 12(e) shows that P(Vy) peaks at Vy = 0.0 and has an overall asymmetry, which also appears in the Vy versus Vx plot in Fig. 12(f). The vortex channeling occurs when the vortices form effective pairs aligned along the x-direction. In each pair, one vortex is slowed by the backward-sloping side of the potential trough, while the other vortex is being sped up by the forward-sloping side of the potential. The faster vortex pushes the slower vortex, giving the pair an increased net motion along the x direction. This pairing effect is visible in the real space image in Fig. 11(c).
As Fd further increases, there is a transition to a flowing solid phase as shown in Fig. 11(e,f) for Fd = 3.6, where S(k) has sixfold ordering. The corresponding P(Vx) in Fig. 12(g) has two peaks, while P(Vy) in Fig. 12(h) has a symmetrical distribution with three peaks indicating that there is an oscillation in the vortex orbits in the x-direction. The plot of Vy versus Vx in Fig. 12(h) contains a single lobe similar to that found for the moving floating solid in Fig. 10(i). As Fd is increased still further, the width of this lobe decreases. The smectic-to-smectic transition is limited to the range 1.5 < w/a < 2, in which two vortices can fit between adjacent potential maxima in the dynamically moving regime.

VI.  DYNAMICAL PHASE DIAGRAM

Fig13.png
Figure 13: (a) Forc, the drive at which the system transitions from a density modulated moving crystal to an ordered moving floating solid, vs w/a at Fp= 0.5 (red circles), 1.0 (green squares), 1.5 (orange diamonds), and 2.0 (black triangles). (b) Dynamic phase diagram as a function of Fd and w/a for a system with Fp=1.5. P: pinned phase. Plastic: plastic flow regime. ML: moving modulated lattice state. MFS: moving flowing solid state. Dashed lines are guides to the eye that indicate the transition from r1 to r2, r2 to r3, and r3 to a disordered pinned state.
For Fp > 0.25, the drive Forc at which the system transitions from a density modulated moving crystal to an ordered moving floating solid shows considerable variation with w/a, particularly for the larger values of Fp. In Fig. 13(a) we plot Forc, determined from the location of a feature in P6, versus w/a for Fp = 0.5, 1.0, 1.5, and 2.0. For Fp = 0.5, Forc has a local maximum near w/a = 2.5, and then drops for w/a > 3.0. In the pinned phase for w/a > 3.0, the system forms a polycrystalline state, and in the moving state the grains realign to form a moving crystalline state. For Fp = 1.0, 1.5, and 2.0, for w/a < 1.75 the system depins from a single chain of vortices and can partially form a moving crystal state. When w/a is large enough that a pinned zig-zag state forms, the moving density-modulated state can persist up to much higher drives. For Fp = 1.0 the system forms a pinned polycrystalline state for w/a > 4.5 which coincides with the drop in Forc for w/a > 4.5. For Fp = 1.5 and 2.0, there are local peaks in Forc that correlate with the moving buckled phases which occur when groups of vortices can fit between adjacent pinning maxima as the vortices move. This effect is most pronounced for Fp = 2.0.
In Fig. 13(b) we plot a dynamic phase diagram as a function of Fd and w/a for a system with Fp = 1.5. Above depinning in the regime where Fd < Fp, the system is in a plastic flow state in which there is a coexistence of moving vortices and immobile vortices. In this regime the structure factor generally shows disordered features. For Fd > Fp, all the vortices are moving and the system is either in a modulated lattice (ML) state or a moving flowing solid (MFS) state. We find similar dynamical phase diagrams for other values of Fp > 1.0, while for the weaker substrates, the size of the plastic flow region is reduced and the ML phase is replaced with a smectic moving state similar to that shown in Fig. 11(c,d).

VII.  DISCUSSION

The dynamic phases we observe have certain similarities to the dynamic states observed for vortices moving over random pinning arrays in that there can be pinned, plastic, and dynamically ordered phases as a function of external drive [86,87,88,89,90,91]. There are some differences, including the fact that the moving modulated lattice we observe does not form a smectic state that is fully aligned in the drive direction, as found for vortices moving over random pinning arrays [88,89,90,91]. Experimental observations of the smectic to smectic phase transition could be achieved using direct dynamical imaging techniques [13,85] or neutron scattering techniques [96]. Voltage noise measurements could also reveal the transitions between the different dynamical phases, as in experiments on samples with random pinning [91,97,98]. The dynamical transitions can be observed if the depinning current is sufficiently far below the depairing current, which will depend on the magnetic field, the strength of the intrinsic pinning, and how close the system is to Tc. According to Fig. 13, the dynamical reordering currents are expected to be 2.5 to 10 times higher than the depinning current, so the accessible current range needs to be at least this wide in order to experimentally observe the dynamical transitions. Simulations with random pinning arrays indicate that for increasing vortex density, the drive at which the transition to the ordered state occurs decreases due to the increase in the strength of the vortex-vortex interactions [91]. For the q1D substrate, the location of the ordering transition fluctuates strongly due to the ability of the moving lattice to become dynamically commensurate with the periodicity of the substrate. Future studies might consider combinations of random disorder with periodic disorder, which would introduce a competition in the moving phase between the smectic ordering imposed by the substrate and the smectic ordering induced by the drive.
We focus on vortices driven along the direction of the substrate periodicity, but it would also be interesting to study the response of the system when the vortices are driven perpendicular or at an arbitrary angle to the substrate periodicity. Previous studies of vortices driven at varied angles through 2D periodic pinning arrays show that the substrate can induce a number of dynamical effects, including directional locking of the vortex motion as well as vortex channeling effects [99,67,100,101,102]. For a q1D substrate, vortices driven at arbitrary angles should exhibit channeling along the substrate troughs, and the drive at which this channeling is overcome and the vortices start to flow in the direction of drive should be a function of driving angle. Measurements of the transverse and longitudinal vortex velocities in this case should show zero velocity in the direction of the substrate periodicity at low drives, and finite velocity both parallel and perpendicular to the driving direction for intermediate drives. Studies of vortices driven over a 1D line potential show channeling effects of this type [102,103].
We consider a particle based model, but simulations based on time-dependent Ginzburg-Landau (TDGL) theory may reveal other interesting behavior for higher fields or currents than we study, such as the elongation of the vortices along certain directions or the formation of multiple-quanta vortices. TDGL studies of vortices in 2D periodic pinning arrays show that a rich variety of commensurate and incommensurate states can form with multi-quanta vortices or combinations of multi-quanta and interstitial vortices [19,20,21,22]. Similar effects could arise for q1D substrates. A TDGL approach could capture additional features in the depinning behavior and subsequent flow such as merging, splitting, elongation, or local heating effects of the vortices [104,105,106,107]. It can also treat the effect of the substrate thickness in the limit of a thin film. Our particle-based model assumes that the vortices experience the same driving force regardless of their position in the sample; however, recent TDGL simulations show that the applied current can be modified by the thickness of the sample, and that the effective viscosity also varies with thickness due to the changing length of the vortex [108,109,110,111]. Such effects could be explored using TDGL simulations or modified particle-based models in which additional terms are introduced to represent the spatial dependence of the viscosity or the applied driving force.

VIII.  SUMMARY

We examine the statics and dynamics of vortices interacting with a periodic quasi-one-dimensional substrate in the limit where the vortex lattice spacing is smaller than the spacing of the periodic lattice. For weak substrate strengths, we find that the vortices retain hexagonal ordering but exhibit numerous rotations with respect to the substrate, similar to recent experimental observations. For stronger substrates there are a series of buckling transitions where the vortices can form anisotropic 1D chains, zig-zag patterns, and higher order numbers of chains within each substrate minimum. At some fillings the overall lattice has long range order and becomes partially distorted at the transitions between these states. For higher fillings the buckling transitions are lost and the system forms a polycrystalline state. We also find that the depinning shows a series of step-like features when the system transitions from a state with n chains to a state with n+1 chains in each substrate minimum, and that for weaker pinning there are some cases where there is a peak in the depinning force as a function of filling. For weak substrates, under an applied drive the vortices depin elastically and retain their triangular ordering, while for strong substrates the buckled states transition to a partially disordered flowing state followed by various other transitions into moving modulated crystal or homogeneous floating moving crystal states. Our results should also be applicable to other systems of particles with repulsive interactions in the presence of a periodic quasi-one dimensional substrate, such as electron crystals, colloids, and ions in optical traps.

ACKNOWLEDGMENTS

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
P. Bak, Commensurate phases, incommensurate phases and the devil's staircase, Rep. Prog. Phys. 45, 587 (1982).
[2]
O.M. Braun and Y.S. Kivshar, The Frenkel-Kontorova Model: Concepts, Methods, and Applications (Springer-Verlag, Berlin, 2004).
[3]
A.D. Novaco and J.P. McTague, Orientational epitaxy - the orientational ordering of incommensurate structures, Phys. Rev. Lett. 38, 1286 (1977).
[4]
S.N. Coppersmith, D.S. Fisher, B.I. Halperin, P.A. Lee, and W.F. Brinkman, Dislocations and the commensurate-incommensurate transition in two dimensions, Phys. Rev. B 25, 349 (1982).
[5]
M. Peyrard and S. Aubry, Critical behaviour at the transition by breaking of analyticity in the discrete Frenkel-Kontorova model, J. Phys. C: Solid State Phys. 16, 1593 (1983).
[6]
S. Bleil, H.H. von Grunberg, J. Dobnikar, R. Castaneda-Priego, and C. Bechinger, Strain-induced domain formation in two-dimensional colloidal systems, Europhys. Lett. 73, 450 (2006).
[7]
T. Bohlein, J. Mikhael, and C. Bechinger, Observation of kinks and antikinks in colloidal monolayers driven across ordered surfaces, Nature Mater. 11, 126 (2012).
[8]
A. Vanossi, N. Manini, and E. Tosatti, Static and dynamic friction in sliding colloidal monolayers, Proc. Natl. Acad. Sci. (USA) 109, 16429 (2012).
[9]
J. Tekic, O.M. Braun, and B.B. Hu, Dynamic phases in the two-dimensional underdamped driven Frenkel-Kontorova model, Phys. Rev. E 71, 026104 (2005).
[10]
A. Vanossi, N. Manini, M. Urbakh, S. Zapperi, and E. Tosatti, Modeling friction: From nanoscale to mesoscale, Rev. Mod. Phys. 85, 529 (2013).
[11]
D. Mandelli, A. Vanossi, N. Manini, and E. Tosatti, Friction boosted by equilibrium misalignment of incommensurate two-dimensional colloid monolayers, Phys. Rev. Lett. 114, 108302 (2015).
[12]
M. Baert, V.V. Metlushko, R. Jonckheere, V.V. Moshchalkov, and Y. Bruynseraede, Composite flux-line lattices stabilized in superconducting films by a regular array of artificial defects, Phys. Rev. Lett. 74, 3269 (1995).
[13]
K. Harada, O. Kamimura, H. Kasai, T. Matsuda, A. Tonomura, and V.V. Moshchalkov, Direct observation of vortex dynamics in superconducting films with regular arrays of defects, Science 274, 1167 (1996).
[14]
J.I. Martín, M. Vélez, J. Nogués, and I.K. Schuller, Flux pinning in a superconductor by an array of submicrometer magnetic dots, Phys. Rev. Lett. 79, 1929 (1997).
[15]
D.J. Morgan and J.B. Ketterson, Asymmetric flux pinning in a regular array of magnetic dipoles, Phys. Rev. Lett. 80, 3614 (1998).
[16]
C. Reichhardt, J. Groth, C. J. Olson, S.B. Field, and F. Nori, Spatiotemporal dynamics and plastic flow of vortices in superconductors with periodic arrays of pinning sites, Phys. Rev. B 54, 16108 (1996).
[17]
C. Reichhardt, C. J. Olson, and F. Nori, Commensurate and incommensurate vortex states in superconductors with periodic pinning arrays, Phys. Rev. B 57, 7937 (1998).
[18]
U. Welp, Z.L. Xiao, V. Novosad, and V.K. Vlasko-Vlasov, Commensurability and strong vortex pinning in nanopatterned Nb films, Phys. Rev. B 71, 014505 (2005).
[19]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Novel commensurability effects in superconducting films with antidot arrays, Phys. Rev. Lett. 96, 207001 (2006).
[20]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Vortex configurations and critical parameters in superconducting thin films containing antidot arrays: Nonlinear Ginzburg-Landau theory, Phys. Rev. B 74, 174512 (2006).
[21]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Superconducting film with weak pinning centers: Incommensurate vortex lattices, Phys. Rev. B 76, 134508 (2007).
[22]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Non commensurate vortex lattices in a composite antidot lattice or dc current, Physica C 468, 809 (2008).
[23]
S. Goldberg, Y. Segev, Y. Myasoedov, I. Gutman, N. Avraham, M. Rappaport, E. Zeldov, T. Tamegai, C.W. Hicks, and K.A. Moler, Mott insulator phases and first-order melting in Bi2Sr2CaCu2O8+δ crystals with periodic surface holes, Phys. Rev. B 79, 064523 (2009).
[24]
I. Swiecicki, C. Ulysse, T. Wolf, R. Bernard, N. Bergeal, J. Briatico, G. Faini, J. Lesueur, and J.E. Villegas, Strong field-matching effects in superconducting YBa2Cu3O7-δ films with vortex energy landscapes engineered via masked ion irradiation, Phys. Rev. B 85, 224502 (2012).
[25]
T.C. Halsey, Josephson-junction arrays in transverse magnetic fields: Ground states and critical currents, Phys. Rev. B 31, 5728 (1985).
[26]
H.D. Hallen, R. Seshadri, A.M. Chang, R.E. Miller, L.N. Pfeiffer, K.W. West, C.A. Murray, and H.F. Hess, Direct spatial imaging of vortices in a superconducting wire network, Phys. Rev. Lett. 71, 3007 (1993).
[27]
J.W. Reijnders and R.A. Duine, Pinning of vortices in a Bose-Einstein condensate by an optical lattice, Phys. Rev. Lett. 93, 060401 (2004).
[28]
H. Pu, L.O. Baksmaty, S. Yi, and N.P. Bigelow, Structural phase transitions of vortex matter in an optical lattice, Phys. Rev. Lett. 94, 190401 (2005).
[29]
S. Tung, V. Schweikhard, and E. A. Cornell, Observation of vortex pinning in Bose-Einstein condensates, Phys. Rev. Lett. 97, 240402 (2006).
[30]
H.P. Büchler, G. Blatter, and W. Zwerger, Commensurate-incommensurate transition of cold atoms in an optical lattice, Phys. Rev. Lett. 90, 130401 (2003).
[31]
B. Gränz, S.E. Korshunov, V.B. Geshkenbein, and G. Blatter, Competing structures in two-dimensional trapped dipolar gases, Phys. Rev. B 90, 060101 (2014).
[32]
A. Benassi, A. Vanossi, and E. Tosatti, Nanofriction in cold ion traps, Nature Commun. 2, 236 (2011).
[33]
A. Bylinskii, D. Gangloff, and V. Vuletic, Tuning friction atom-by-atom in an ion-crystal simulator, Science 348, 6239 (2015).
[34]
K. Mangold, P. Leiderer, and C. Bechinger, Phase transitions of colloidal monolayers in periodic pinning arrays, Phys. Rev. Lett. 90, 158302 (2003).
[35]
S. El Shawish, J. Dobnikar, and E. Trizac, Colloidal ionic complexes on periodic substrates: Ground-state configurations and pattern switching, Phys. Rev. E 83, 041403 (2011).
[36]
D. McDermott, J. Amelang, L.M. Lopatina, C.J. Olson Reichhardt, and C. Reichhardt, Domain and stripe formation between hexagonal and square ordered fillings of colloids on periodic pinning substrates, Soft Matter 9, 4607 (2013).
[37]
T. Neuhaus, M. Marechal, M. Schmiedeberg, and H. Löwen, Rhombic preordering on a square substrate, Phys. Rev. Lett. 110, 118301 (2013).
[38]
J. Mikhael, J. Roth, L. Helden, and C. Bechinger, Archimedean-like tiling on decagonal quasicrystalline surfaces, Nature 454, 501 (2008).
[39]
J. Mikhael, G. Gera, T. Bohlein, and C. Bechinger, Phase behavior of colloidal monolayers on quasiperiodic substrates, Soft Matter 7, 1352 (2011).
[40]
Direct imaging of commensurate vortex structures in ordered antidot arrays A. N. Grigorenko, G. D. Howells, S. J. Bending, J. Bekaert, M. J. Van Bael, L. Van Look, V. V. Moshchalkov, Y. Bruynseraede, G. Borghs, I. I. Kaya, and R. A. Stradling Phys. Rev. B 63, 052504 (2001)
[41]
S. Field, S. James, J. Barentine, V. Metlushko, G. Crabtree, H. Shtrikman, B. Ilic, and S. Brueck, Vortex configurations, matching, and domain structure in large arrays of artificial pinning centers, Phys. Rev. Lett. 88, 067003 (2002).
[42]
A.N. Grigorenko, S.J. Bending, M.J. Van Bael, M. Lange, V.V. Moshchalkov, H. Fangohr, and P.A.J. de Groot, Symmetry locking and commensurate vortex domain formation in periodic pinning arrays, Phys. Rev. Lett. 90, 237001 (2003).
[43]
M. Baert, V.V. Metlushko, R. Jonckheere, V.V. Moshchalkov, and Y. Bruynseraede, Flux phases and quantized pinning force in superconductor with a periodic lattice of pinning centres, Europhys. Lett. 29, 157 (1995).
[44]
C. Reichhardt and N. Grønbech-Jensen, Critical currents and vortex states at fractional matching fields in superconductors with periodic pinning, Phys. Rev. B 63, 054510 (2001).
[45]
D. McDermott, J. Amelang, C.J. Olson Reichhardt, and C. Reichhardt, Dynamic regimes for driven colloidal particles on a periodic substrate at commensurate and incommesnurate fillings, Phys. Rev. E 88, 062301 (2013).
[46]
A. Chowdhury, B.J. Ackerson, and N.A. Clark, Laser-induced freezing, Phys. Rev. Lett. 55, 833 (1985).
[47]
J. Chakrabarti, H.R. Krishnamurthy, A.K. Sood, and S. Sengupta, Reentrant melting in laser field modulated colloidal suspensions, Phys. Rev. Lett. 75, 2232 (1995).
[48]
J. Hu and R.M. Westervelt, Commensurate-incommensurate transitions in magnetic bubble arrays with periodic line pinning, Phys. Rev. B 55, 771 (1997).
[49]
Q.-H. Wei, C. Bechinger, D. Rudhardt, and P. Leiderer, Experimental study of laser-induced melting in two-dimensional colloids, Phys. Rev. Lett. 81, 2606 (1998).
[50]
E. Frey, D. Nelson, and L. Radzihovsky, Light-induced melting of colloidal crystals in two dimensions, Phys. Rev. Lett. 83, 2977 (1999).
[51]
C. Richter, M. Schmiedeberg, and H. Stark, A colloidal model system with tunable disorder: Solid-fluid transition and discontinuities in the limit of zero disorder, Eur. Phys. J. E 34, 107 (2011).
[52]
L. Zaidouny, T. Bohlein, R. Roth, and C. Bechinger, Light-induced phase transitions of colloidal monolayers with crystalline order, Soft Matter 9, 9230 (2013).
[53]
O. Daldini, P. Martinoli, J. L. Olsen, and G. Berner, Vortex-line pinning by thickness modulation of superconducting films, Phys. Rev. Lett. 32, 218 (1974).
[54]
P. Martinoli, O. Daldini, C. Leemann, and E. Stocker, A.C. quantum interference in superconducting films with periodically modulated thickness, Solid State Commun. 17, 205 (1975).
[55]
P. Martinoli, Static and dynamic interaction of superconducting vortices with a periodic pinning potential, Phys. Rev. B 17, 1175 (1978).
[56]
O.V. Dobrovolskiy, E. Begun, M. Huth, and V.A. Shklovskij, Electrical transport and pinning properties of Nb thin films patterned with focused ion beam-milled washboard nanostructures, New J. Phys. 14, 113027 (2012).
[57]
O.V. Dobrovolskiy and M. Huth, Dual cut-off direct current-tunable microwave low-pass filter on superconducting Nb microstrips with asymmetric nanogrooves, Appl. Phys. Lett. 106, 142601 (2015).
[58]
D. Jaque, E.M. González, J.I. Martin, J.V. Anguita, and J. L. Vicent, Anisotropic pinning enhancement in Nb films with arrays of submicrometric Ni lines, Appl. Phys. Lett. 81, 2851 (2002).
[59]
O.V. Dobrovolskiy, AC quantum interference effects in nanopatterned Nb microstrips, J. Supercond. Novel Mag. 28, 469 (2015).
[60]
J. Guimpel, L. Civale, F. de la Cruz, J. M. Murduck, and I.K. Schuller, Dimensional phase transition in superconductors with short coherence length, Phys. Rev. B 38, 2342 (1988).
[61]
S.H. Brongersma, E. Verweij, N.J. Koeman, D.G. de Groot, R. Griessen, and B.I. Ivlev, Phys. Rev. Lett. 71, 2319 (1993).
[62]
L.S. Levitov, Phyllotaxis of flux lattices in layered superconductors, Phys. Rev. Lett. 66, 224 (1991).
[63]
L. Balents and D.R. Nelson, Quantum smectic and supersolid order in helium films and vortex arrays, Phys. Rev. B 52, 12951 (1995).
[64]
N. Fogel, M. Mikhailov, Y. Bomze, and O. Yuzephovich, Intrinsic pinning, commensurability, and reentrant behavior on superconducting Mo/Si multilayers, Phys. Rev. B 59, 3365 (1999).
[65]
S. Baily, B. Maiorov, H. Zhou, F. Balakirev, M. Jaime, S. Foltyn, and L. Civale, Smectic vortex phase in optimally doped YBa2Cu3O7 thin films, Phys. Rev. Lett. 100, 027004 (2008).
[66]
P.J.W. Moll, L. Balicas, X. Zhu, H.-H. Wen, N.D. Zhigadlo, J. Karpinski, and B. Batlogg, Critical current oscillations in the intrinsic hybrid vortex state of SmFeAs(O,F), Phys. Rev. Lett. 113, 186402 (2014).
[67]
A.V. Silhanek, L. Van Look, S. Raedts, R. Jonckheere, and V.V. Moshchalkov, Guided vortex motion in superconductors with a square antidot array, Phys. Rev. B 68, 214504 (2003).
[68]
G. Carneiro, Equilibrium vortex-line configurations and critical currents in thin films under a parallel field, Phys. Rev. B 57, 6077 (1998).
[69]
J.J. Barba and J. Albino Aguiar, Bi-dimensional chain-like vortex structure in a mesoscopic superconductor, J. Phys.: Conf. Ser. 150, 052015 (2009).
[70]
G. Karapetrov, M. Milosevic, M. Iavarone, J. Fedor, A. Belkin, V. Novosad, and F. Peeters, Transverse instabilities of multiple vortex chains in magnetically coupled NbSe2/permalloy superconductor/ferromagnet bilayers, Phys. Rev. B 80, 180506 (2009).
[71]
G. Piacente, I.V. Schweigert, J.J. Betouras, and F.M. Peeters, Generic properties of a quasi-one-dimensional classical Wigner crystal, Phys. Rev. B 69, 045324 (2004).
[72]
J.E. Galván-Moya and F.M. Peeters, Ginzburg-Landau theory of the zigzag transition in quasi-one-dimensional classical Wigner crystals, Phys. Rev. B 84, 134106 (2011).
[73]
J.E. Galván-Moya, V.R. Misko, and F.M. Peeters, Generic ordering of structural transitions in quasi-one-dimensional Wigner crystals, Phys. Rev. B 90, 094111 (2014).
[74]
W. Ferreira, J. Carvalho, P. Oliveira, G. Farias, and F. Peeters, Structural and dynamical properties of a quasi-one-dimensional classical binary system, Phys. Rev. B 77, 014112 (2008).
[75]
D. Lucena, W.P. Ferreira, F.F. Munarin, G.A. Farias, and F.M. Peeters, Tunable diffusion of magnetic particles in a quasi-one-dimensional channel, Phys. Rev. E 87, 012307 (2013).
[76]
A.V. Straube, R.P.A. Dullens, L. Schimansky-Geier, and A.A. Louis, Zigzag transitions and nonequilibrium pattern formation in colloidal chains, J. Chem. Phys. 139, 134908 (2013).
[77]
J.E. Galván-Moya, D. Lucena, W.P. Ferreira, and F.M. Peeters, Magnetic particles confined in a modulated channel: Structural transitions tunable by tilting a magnetic field, Phys. Rev. E 89, 032309 (2014).
[78]
B. Liu and J. Goree, Phonons in a one-dimensional Yukawa chain: Dusty plasma experiment and model, Phys. Rev. E 71, 046410 (2005).
[79]
T.E. Sheridan and A.L. Magyar, Power law behavior of the zigzag transition in Yukawa clusters, Phys. Plasmas 17, 113703 (2010).
[80]
S. Fishman, G. De Chiara, T. Calarco, and G. Morigi, Structural phase transitions in low-dimensional ion crystals, Phys. Rev. B 77, 064111 (2008).
[81]
A. del Campo, G. De Chiara, G. Morigi, M.B. Plenio, and A. Retzker, Structural defects in ion chains by quenching the external potential: the inhomogeneous Kibble-Zurek mechanism, Phys. Rev. Lett. 105, 075701 (2010).
[82]
M. Mielenz, J. Brox, S. Kahra, G. Leschhorn, M. Albert, T. Schaetz, H. Landa, and B. Reznik, Trapping of topological-structural defects in Coulomb crystals, Phys. Rev. Lett. 110, 133004 (2013).
[83]
J.-B. Delfau, C. Coste, and M. Saint Jean, Transverse single-file diffusion near the zigzag transition, Phys. Rev. E 87, 032163 (2013).
[84]
T. Dessup, T. Maimbourg, C. Coste, and M. Saint Jean, Linear instability of a zigzag pattern, Phys. Rev. E 91, 022908 (2015)
[85]
I. Guillamón, R. Córdoba, J. Sesé, J.M. De Teresa, M.R. Ibarra, S. Vieira, and H. Suderow, Enhancement of long-range correlations in a 2D vortex lattice by an incommensurate 1D disorder potential, Nature Phys. 10, 851 (2014).
[86]
S. Bhattacharya and M.J. Higgins, Dynamics of a disordered flux line lattice, Phys. Rev. Lett. 70, 2617 (1993).
[87]
A.E. Koshelev and V.M. Vinokur, Dynamic melting of the vortex lattice, Phys. Rev. Lett. 73, 3580 (1994).
[88]
L. Balents, M.C. Marchetti, and L. Radzihovsky, Nonequilibrium steady states of driven periodic media, Phys. Rev. B 57, 7705 (1998).
[89]
P. Le Doussal and T. Giamarchi, Moving glass theory of driven lattices with disorder, Phys. Rev. B 57, 11356 (1998).
[90]
F. Pardo, F. de la Cruz, P.L. Gammel, E. Bucher, and D.J. Bishop, Observation of smectic and moving-Bragg-glass phases in flowing vortex lattices, Nature (London) 396, 348 (1998).
[91]
C.J. Olson, C. Reichhardt, and F. Nori, Nonequilibrium dynamic phase diagram for vortex lattices, Phys. Rev. Lett. 81, 3757 (1998).
[92]
C. Reichhardt, C.J. Olson, and F. Nori, Dynamic phases of vortices in superconductors with periodic pinning, Phys. Rev. Lett. 78, 2648 (1997).
[93]
J. Gutierrez, A.V. Silhanek, J. Van de Vondel, W. Gillijns, and V. Moshchalkov, Transition from turbulent to nearly laminar vortex flow in superconductors with periodic pinning, Phys. Rev. B 80, 140514 (2009).
[94]
J.E. Villegas, S. Savel'ev, F. Nori, E.M. Gonzalez, J.V. Anguita, R. García, and J.L. Vicent, A superconducting reversible rectifier that controls the motion of magnetic flux quanta, Science 302, 1188 (2003).
[95]
A. I. Larkin and Yu. N. Ovchinnikov, Nonlinear effects during the motion of vortices in supercoductors, Zh. Eksp. Teor. Fiz. 68, 1915 (1975) [Sov. Phys. JETP 41, 960 (1976)].
[96]
M.R. Eskildsen, K. Harada, P.L. Gammel, A.B. Abrahamsen, N.H. Andersen, G. Ernst, A.P. Ramirez, D.J. Bishop, K. Mortensen, D. G. Naugle, K.D.D. Rathnayaka, and P.C. Canfield, Intertwined symmetry of the magnetic modulation and the flux-line lattice in the superconducting state of TmNi2B2C, Nature 393, 242 (1998).
[97]
A.C. Marley, M.J. Higgins, and S. Bhattacharya, Flux flow noise and dynamical transitions in a flux line lattice, Phys. Rev. Lett. 74, 3029 (1995).
[98]
S. Okuma, K. Kashiro, Y. Suzuki, and N. Kokubo, Order-disorder transition of vortex matter in a-MoxGe1-x films probed by noise, Phys. Rev. B 77, 212505 (2008).
[99]
C. Reichhardt and F. Nori, Phase locking, devil's staircases, Farey trees, and Arnold tongues in driven vortex lattices with periodic pinning, Phys. Rev. Lett. 82, 414 (1999).
[100]
J.E. Villegas, E.M. Gonzalez, M.I. Montero, I.K. Schuller, and J.L. Vicent, Directional vortex motion guided by artificially induced mesoscopic potentials, Phys. Rev. B 68, 224504 (2003).
[101]
C. Reichhardt and C. J. Olson Reichhardt, Switching and jamming transistor effect for vortex matter in honeycomb pinning arrays with ac drives, Phys. Rev. B 81, 024510 (2010).
[102]
C. Reichhardt, C.J. Olson, and F. Nori, Dynamic vortex phases and pinning in superconductors with twin boundaries, Phys. Rev. B 61, 3665 (2000).
[103]
V. Shklovskij, Guiding of vortices and the Hall conductivity scaling in a bianisotropic planar pinning potential, Phys. Rev. B 65, 092508 (2002).
[104]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Vortex lattice in effective type-I superconducting films with periodic arrays of submicron holes, Physica C 437-438, 28 (2006).
[105]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Kinematic vortex-antivortex lines in strongly driven superconducting stripes, Phys. Rev. B 79, 184506 (2009).
[106]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Tunable kinematics of phase-slip lines in a superconducting stripe with magnetic dots, Phys. Rev. B 80, 214509 (2009).
[107]
A.V. Silhanek, M.V. Milosevic, R.B.G. Kramer, G.R. Berdiyorov, J. Van de Vondel, R.F. Luccas, T. Puig, F.M. Peeters, and V.V. Moshchalkov, Formation of stripelike flux patterns obtained by freezing kinematic vortices in a superconducting Pb film, Phys. Rev. Lett. 104, 017001 (2010).
[108]
G.R. Berdiyorov, M.V. Milosevic, B.J. Baelus, and F.M. Peeters, Superconducting vortex state in a mesoscopic disk containing a blind hole, Phys. Rev. B 70, 024508 (2004).
[109]
G.R. Berdiyorov, V.R. Misko, M.V. Milosevic, W. Escoffier, I.V. Grigorieva, and F.M. Peeters, Pillars as antipinning centers in superconducting films, Phys. Rev. B 77, 024526 (2008).
[110]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Composite vortex ordering in superconducting films with arrays of blind holes, New J. Phys. 11, 013025 (2009).
[111]
V.N. Gladilin, J. Ge, J. Gutierrez, M. Timmermans, J. Van de Vondel, J. Tempere, J.T. Devreese, and V.V. Moshchalkov, Vortices in a wedge made of a type-I superconductor, New J. Phys. 17, 063032 (2015).


File translated from TEX by TTHgold, version 4.00.
 Back to Home