Physical Review E 99, 042601 (2019)

Dynamic Phases, Stratification, Laning, and Pattern Formation for Driven Bidisperse Disk Systems in the Presence of Quenched Disorder

D. McDermott1,2, Y. Yang1,3, C. J. Olson Reichhardt1, and C. Reichhardt1

1Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Department of Physics, Pacific University, Forest Grove, Oregon 97116, USA
3School of Physics and Astronomy, University of Minnesota, Minneapolis, Minnesota 55455, USA

(Received 17 September 2018; revised manuscript received 25 February 2019; published 2 April 2019)

Using numerical simulations, we examine the dynamics of driven two-dimensional bidisperse disks flowing over quenched disorder. The system exhibits a series of distinct dynamical phases as a function of applied driving force and packing fraction including a phase separated state as well as a smectic state with liquid like or polycrystalline features. At low driving forces, we find a clogged phase with an isotropic density distribution, while at intermediate driving forces the disks separate into bands of high and low density with either liquid like or polycrystalline structure in the high density bands. In addition to the density phase separation, we find that in some cases there is a fractionation of the disk species, particularly when the disk size ratio is large. The species phase separated regimes form a variety of patterns such as large disks separated by chains of smaller disks. Our results show that the formation of laning states can be enhanced by tuning the ratio of disk radius of the two species, due to the clumping of small disks in the interstitial regions between the large disks. This system could be experimentally realized using sterically interacting colloidal particles suspended in a viscous fluid driven over random pinning arrays or granular matter suspended in fluid moving over a random landscape.
I. INTRODUCTION
II. SIMULATION
III. MINIMALLY PHASE SEPARATING SYSTEM WITH Nl=Nd/2
A. Intermediate disk densities
B. High disk density
C. Transverse diffusion and topological order
IV. ENHANCED CRYSTALLIZATION AND BANDING WITH LARGER RADIUS RATIO AT Nl=Nd/2
Transverse diffusion and topological order
V. LOWER FRACTION OF LARGE DISKS, Nl=Nd/10
VI. SCALING NEAR THE DEPINNING TRANSITION
VII. CONTINUOUS DRIVING FORCE
VIII. DISCUSSION
X. SUMMARY
REFERENCES

I.  INTRODUCTION

A large class of systems can be effectively described as a collection of interacting particles moving over a random pinning landscape, where a variety of distinct dynamical phases appear as a function of driving force [1]. Well studied examples of such systems include vortices in type-II superconductors [2,3,4,5,6], driven Wigner crystals [7,8], skyrmions undergoing current-induced motion [9,10,11], sliding pattern forming assemblies coupled to random landscapes [12,13], colloids on disordered substrates [14,15,16,17,18,19], and active matter moving in complex environments [20,21,22]. These systems often exhibit multiple nonequilibrium phase transitions, such as a transition from a pinned to a sliding phase followed by transitions to different types of sliding phases. Such transitions are associated with clearly observable changes in the velocity-force curves, fluctuation spectra, and spatial reordering of the particles.
Previous work on dynamical phase transitions in driven systems has primarily focused on long or intermediate range particle-particle interactions that tend to favor a uniform particle density, such as that found in magnetic or charged systems. When particles of this type are placed on quenched disorder composed of randomly placed strong pinning sites, three nonequilibrium phases emerge: a pinned disordered state, a plastic flow state in which the particle positions are disordered and the particles exchange neighbors as they move, and a dynamically reordered anisotropic crystal or moving smectic state that appears at high drives when the effectiveness of the pinning is reduced [1].
There are numerous examples of systems in which the particle-particle interactions are short ranged or steric, including many types of colloidal suspensions, emulsions, bubbles, and granular matter. Although it might be natural to assume that the short-range interactions would produce simpler behavior than the longer-range interactions when the particles are driven over quenched disorder, it was recently shown that monodisperse hard disks moving over a random pinning landscape exhibit a remarkably rich variety of dynamical phases, including clogging, disordered plastic flow, segregated flow, laning flow, and moving crystals [23]. The disk system can form moving density segregated states containing high density bands coexisting with low density regions. In some cases, the dense bands form close packed hexagonal lattices even when the overall density of the system is well below the crystallization density. At higher drives, the crystalline bands break up to form dense one-dimensional chains, while at higher densities the disks form a moving crystalline solid [23]. Density separated phases cost no energy in systems with contact interactions, since the energy remains small even when the particles accumulate in one region and are depleted from another region. In contrast, when the interactions are longer range, the system can minimize its energy by destabilizing and dispersing any locally dense regions.
In this work, we consider bidisperse disks driven over quenched disorder consisting of randomly placed pinning sites. In the absence of driving or pinning, the disks form a jammed solid at densities well below the crystallization density ϕ = 0.9 of pin-free undriven monodisperse disks [24,25]. Both monodisperse and bidisperse disks can exhibit a density segregation into dense and depleted regions, but the bidisperse disks can also undergo species segregation of the two disk sizes. Numerous studies have demonstrated species segregation under nonequilibrium conditions for short range repulsive bidisperse systems including granular matter [26,27,28,29] and colloids [30,31,32], where the degree of segregation depends on the ratio of particle sizes and the type of driving force applied. There are, however, few studies examining the impact of quenched disorder on size segregation. An understanding of segregation effects in flowing bidisperse disks coupled to quenched disorder not only offers new insights on depinning and sliding phenomena, but also could be used to develop new methods for separating or mixing bidisperse or polydisperse systems of particles. For example, some geological systems can be described in terms of polydisperse disks moving through random pinning, and such systems could undergo dynamic segregation. Furthermore, these results could be relevant to experiments in multi-species flows of soft matter confined to quasi-two dimensional environments, such as sterically interacting colloids moving over random substrates or the flow of granular matter over a disordered background.
This paper is organized as follows. We describe our simulation technique for the bidisperse disks driven over random pinning in Section II. In Section III, we show the dynamic patterns that form for a system in which 50% of the disks are large and the radius ratio of the large to small disks is 1.4. In Section IV, we consider large disks that are twice as big as the smaller disks while maintaining the fraction of large disks at 50%. In Section V, we show that by reducing the fraction of large disks to 10%, we can enhance the segregation and stratification effects. We examine the scaling of the velocity-force curves near depinning in Section VI. We test for hysteresis in Section VII, and we discuss possible extensions to the simulations in Section VIII. We summarize our results in Section IX.

II.  SIMULATION

We consider a two dimensional (2D) system of size L ×L with periodic boundary conditions in the x and y directions. The sample contains Nd=Ns+Nl disks, where Ns disks have a small radius of rs and Nl disks have a large radius of rl. The disk dynamics are governed by the following overdamped equation of motion:
η d Ri
dt
 = Fdd + Fp + FD .
(1)
Here η is the damping constant and Ri is the location of disk i. The disk-disk interaction force is Fdd = ∑i ≠ jk(rddij − Rij)Θ(rddij − Rij) ∧Rij, where rddij=ri+rj, ri(j) is the radius of disk i(j), Rij = |Ri − Rj|, ∧Rij = (Ri−Rj)/Rij, Θ is the Heaviside step function, and the spring constant k = 50 is large enough to prevent the disks from overlapping by more than 1% of their radii. The pinning force Fp is produced by Np pinning sites modeled as randomly placed non-overlapping parabolic wells cut off at a radius of rp=rs that can each capture at most one disk with a maximum pinning force of Fp=1.0. The density ϕ of the system is given by the area covered by the disks, ϕ = π(Ns r2s+Nl r2l)/L2, where L = 60 and rs = 0.5. We vary rl and set the radius ratio Ψ = rl/rs to Ψ = 1.4 in Sec. III and Ψ = 2.0 in Sec. IV. In a previous study of the jamming of bidisperse disks using this model with Ψ = 1.4, the jamming density in a pin free sample is ϕj ≈ 0.845 [33]. We set Np=1440, giving a fixed pinning site density of ϕp = Np πrp2/L2=0.31. Previous studies have shown that increasing ϕp does not alter the behavior, but only shifts the driving forces at which the dynamical transitions occur [23]. The driving force FD=FD∧x is applied uniformly to all disks. We perform a series of separate runs for each value of FD at intervals of ∆FD=0.05. In Sec. VII, we perform a continuous sweep of FD over the range 0 to 2.0 and find that the results are essentially identical with those obtained for the series of individual runs at each FD value. On each drive increment, we measure the species-dependent disk velocities, 〈Vxs〉 = Nd−1∑Ndi=1(vi ·∧x)δ(ri−rs) and 〈Vxl〉 = Nd−1∑Ndi=1(vi ·∧x)δ(ri−rl), where vi is the instantaneous velocity of disk i. We generate species-dependent histograms of P(vx), the distribution of velocities vx of the individual disks in the direction of applied drive, by first allowing the system to reach a steady state and then sampling the velocities every ∆t = 5 ×105 simulation time steps. The corresponding P(vy) is Gaussian distributed about vy=0 since the motion of the disks perpendicular to the driving force is unbiased. We also characterize the dynamic phases and phase transitions using velocity-force curves, the transverse root mean square displacements, and other measures of the particle spacing and density. The measurements are time-averaged over a single realization of disorder. We have checked that performing disorder averaging does not change the results except very close to the critical point, as described in Section VII.

III.  MINIMALLY PHASE SEPARATING SYSTEM WITH Nl=Nd/2

Fig1.png
Figure 1: (a) The species-dependent average disk velocities 〈Vxs 〉 (solid lines) and 〈Vxl 〉 (dashed lines) versus driving force FD/Fp in a sample with Ψ = 1.4 with equal numbers of small and large disks, Ns=Nl. The total disk density is ϕ = 0.87 (down triangles), 0.81 (pentagons), 0.70 (right triangles), 0.58 (stars), 0.46 (squares), 0.35 (up triangles), and 0.23 (circles). (b) The corresponding d〈Vxs〉/dFD (solid lines) and d〈Vxl〉/dFD (dashed lines) vs FD/Fp curves for the same values of ϕ showing a peak near FD/Fp=1.0. Inset: critical depinning force Fc vs disk density ϕ. (c) The difference ∆〈Vx 〉 = 〈Vxs〉− 〈Vxl 〉 vs FD/Fp for the same values of ϕ shown in panels (a) and (b).
We first consider samples with Ns=Nl and a disk diameter ratio of Ψ = 1.4. By varying the disk density from ϕ = 0.23 to ϕ = 0.81, we obtain a ratio of pinning sites to disks in the range Np/Nd = 2.0 to 0.53. At ϕ = 0.46 there is one disk for every pin, Np/Nd = 1.0. In Fig. 1(a) we plot 〈Vxs〉 and 〈Vxl〉 versus FD/Fp for ϕ = 0.23 to 0.87, and we show the corresponding d〈Vxs〉/dFD and d〈Vxl〉/dFD versus FD/Fp curves in Fig. 1(b). At small FD/Fp, the system is in the pinned or clogged state that we term phase I, while for FD/Fp ≥ 1.5, the velocities increase linearly with drive for all values of ϕ. In the inset of Fig. 1(b) we plot the critical depinning force Fc marking the end of phase I versus ϕ. When ϕ is low, Fc ≈ Fp since each disk can be captured independently by a pinning site. As the disk density increases, Fc drops when the disks begin to interact with each other. Since each pin can capture at most one disk, if an unpinned disk comes into contact with a pinned disk, the driving force on both disks is offset by the pinning force on only one disk, lowering the depinning threshold. The number of disks in contact with each other increases with increasing ϕ, causing Fc to decrease monotonically. We find no species dependence of Fc at any value of ϕ. Figure 1(c) shows ∆〈Vx 〉 = 〈Vxs〉− 〈Vxl〉, the difference in net velocity between the two disk species. This difference is largest in magnitude near the depinning transition.
At a small disk density of ϕ = 0.23 in Fig. 1, both 〈Vxs 〉 and 〈Vxl〉 show relatively sharp depinning transitions, as also indicated by the large single peak at depinning in the d 〈Vxs〉/dFD and d 〈Vxl〉/dFD versus FD/Fp curves. For drives close to but above Fc, the smaller disks move slightly faster than the larger disks so that ∆〈Vx〉 > 1.

A.  Intermediate disk densities

Fig2.png
Figure 2: (a, b, c, d) Left panels: Large disk (blue circles) and small disk (red circles) positions for the system in Fig. 1 with Ψ = 1.4 and Ns=Nl at ϕ = 0.35. Center panels: nlloc (blue) and nsloc (red), the local number density of large and small disks, respectively, averaged over the x direction for each y position. Right panels: ∆nloc=nsloc−nlloc plotted at each y position. (a) The pinned phase I at FD/Fp=0.3, where unpinned disks pile up behind pinned disks. (b) Just above depinning at FD/Fp=0.9 in phase III, where the sample contains a dense liquid-like region in the center surrounded by a gas-like region. (c) FD/Fp=1.1 in phase IV flow, where the small and large disks become further segregated and the disks from the gas-like region collapse into chains with smectic ordering. (d) FD/Fp=2.0 in phase V, where the entire sample develops a smectic structure. (e) Detail showing large disk (blue circles), small disk (red circles), and pinning site (gray circles) locations in a portion of the sample from panel (c) at FD/Fp=1.1 in phase IV. (f) Detail as in (e) for a portion of the sample from panel (d) at FD/Fp=2.0 in phase V.
Disk-disk interactions become important at ϕ = 0.35, where Fig. 1(b) shows that a two peak structure emerges in d 〈Vxs〉/dFD, with one peak at FD/Fp=0.9 and a smaller second peak at FD/Fp=1.05. We also find that d 〈Vxl〉/dFD has a small peak at FD/Fp=0.7 and a larger peak at FD/Fp=1.05. A positive peak in ∆〈Vx〉 extends over the range 0.8 < FD/Fp < 1.05 and is larger in magnitude than what we observe at other values of ϕ.
In the left panel of Fig. 2(a) we illustrate the disk positions in the pinned phase I for ϕ = 0.35 at FD/Fp=0.3. Here, small numbers of unpinned disks have accumulated behind pinned disks, giving a heterogeneous disk density and reducing the depinning threshold to Fc/Fp=0.7. In some regions, short chains of disks composed preferentially of large disks are stabilized at an angle to the driving direction. In the center panel of Fig. 2(a) we plot the local number density nlloc and nsloc of large and small disks, respectively, obtained by taking slices of width w=4rs through the sample at a fixed value of y and dividing the number of disks of each type in that slice by the slice area. Thus, nsloc(y)=(4rsL)−1∑iNs Θ(|Ryi−y|−2rs)δ(ri−rs) and nlloc(y)=(4rsL)−1∑iNl Θ(|Ryi−y|−2rs)δ(ri−rl). The difference in local number density, ∆nloc=nlloc−nsloc, is shown as a function of y in the rightmost panel of Fig. 2(a). Below the depinning transition, both disk species are distributed uniformly throughout the sample.
Fig3.png
Figure 3: Histograms of P(vx) for the velocity vx parallel to the driving direction for the small disks (red) and large disks (blue) for the system in Fig. 1 at ϕ = 0.35 with (a) FD/Fp = 0.9 in phase III and (b) FD/Fp=1.1 in phase IV.
Figure 1(c) shows that for ϕ = 0.35 at FD/Fp = 0.9, the velocity of the small disks is larger than that of the large disks, giving ∆〈Vx〉 ≈ 0.24. At this drive the sample develops a horizontal band containing a high local density of small disks moving through a homogeneous distribution of large disks, forming a phase separated liquid-gas state illustrated in Fig. 2(b) that we term phase III. The peak in d〈Vxs〉/dFD at FD/Fp=0.9 coincides with the emergence of the dense band of small disks in the region 10 < y < 45. At y=30 the value of nlloc is nearly zero, but in the rest of the sample nlloc is roughly constant. The small disks flow continuously while the large disks undergo stick-slip motion that is enhanced in the vicinity of the band of small disks, as shown in the supplementary video [34]. The species-dependent velocity distributions P(vx) in Fig. 3(a) show that vx is bimodal for each species, with peaks at vx = 0 and vx=0.9 arising from the alternating pinned and freely flowing motion of each disk. The vx=0.9 peak is higher for the small disks than for the large disks since the small disks are more likely to move freely due to their separation into a dense band, and similarly the peak at vx=0 is highest for the large disks, which are more likely to fall into a pinning site due to their greater radius. Strong interactions with the pinning sites are required to produce the vx=0 peak. Although P(vx) falls off rapidly above vx=FD=0.9, there is still a tail with finite weight at vx > FD produced by disks that undergo brief rapid motion just after escaping from a pinning site.
In Fig. 2(c) at FD/Fp=1.1, the band of small disks in the ϕ = 0.35 system becomes more diffuse. Simultaneously, the large disks segregate into dense bands surrounding the original band of small disks, while the lower density portion of the sample develops smectic ordering consisting of chains of mixed disk sizes that are oriented with the driving direction. We call this phase separated liquid-smectic state phase IV. Figure 1(c) shows that 〈Vxs〉 is slightly larger than 〈Vxl〉 at this drive since the higher density band of small disks is able to move more efficiently over the pinning sites, as illustrated in the supplemental video [35]. Figure 2(e) shows a more detailed plot of the disk positions along with the pinning site locations in a portion of the sample from Fig. 2(c) containing both the dense band of large disks and the smectic chains. The disk species are not segregated within the chains, and since the pinning force and driving force are nearly equal, the disks do not experience much transverse displacement as they traverse the pinning sites. In the liquid-smectic phase IV, P(vx) has a single peak at vx=1.1 with equal weight for both species, as shown in Fig. 3(b). Interactions of the disks with the pins in the lower density portions of the sample produce a broad plateau in P(vx) over the range 0.1 < vx < 1.1. Since FD > Fp, the pinning sites can only slow the disks but cannot trap them, so there is no longer a peak at vx=0.
At higher drives for ϕ = 0.35, the system enters phase V in which the smectic ordering spreads throughout the entire sample, as shown in Fig. 2(d) at FD/Fp=2.0. The tendency of the disks to form chains in this state is illustrated in a detailed view in Fig. 2(f). Chainlike ordering emerges continuously in the smectic state as the drive increases. The long chains of disks have greater species separation and reduced fluctuations in the y direction compared to the chains which form at lower FD. The dynamics of this state are illustrated in the supplemental movie [36]. Similar lane formation was observed for a low density of monodisperse disks driven over quenched disorder [23], and is due in part to the fact that strong density modulations incur no energy penalty in systems with short range interactions. Although on average ∆nloc ≈ 0, indicating that the large scale species segregation found at lower drives is lost, we find that individual chains can be preferentially composed of a single species of disk. The velocity distributions P(vx) are similar to those shown in Fig. 3(b) but have a sharper peak at vx = FD.
The moving smectic state we observe differs from that predicted by theory[38,39] and observed in simulations [6,40,41] and experiments [5] to occur in driven systems with quenched disorder such as vortices in type-II superconductors confined to two dimensions. The short-range nature of the disk-disk interactions permits the emergence of extreme chaining behavior in which the disks are nearly in contact along the driving direction but are well-spaced in the transverse direction. In contrast, superconducting vortices strongly repel one another at short distances, and thus have a more even spacing in the directions parallel and transverse to the drive. Adjacent vortex rows in the smectic state contain dislocations that can glide along the driving direction and permit the rows to slide past one another. For the disk system, adjacent rows are noninteracting and can move completely independently of each other.
Fig4.png
Figure 4: (a) The instantaneous disk velocity Vxs (solid lines) and Vxl (dashed lines) versus time for the small and large disks, respectively, in the sample from Fig. 1 at ϕ = 0.35 for FD=0.7 (phase I), 0.8 (phase II), 0.9, 0.95, 1.0, 1.05 (phase III), 1.1, and 1.15 (phase IV), from bottom to top. (b) The corresponding ratio R=Vxs/Vxl vs time for samples with FD/Fp > 0.7. (c) Vxs (solid blue line) vs time for the system in panels (a) and (b) at FD = 0.9 in phase III. Black dashed line: A fit to Vxs ∝ e−t/τ with τ = 1.22 ×107. Red dot-dashed line: A fit to Vxs ∝ tα with α = 0.26 ±0.01.
In Fig. 4 we illustrate the time-dependent behavior of the ϕ = 0.35 system. We find similar behavior when 0.2 < ϕ < 0.5. Figure 4(a) shows the instantaneous values of Vxs and Vxl versus time at driving forces ranging from FD/Fp = 0.70 to 1.15. In Fig. 4(b), we show the corresponding ratio R = Vxs/Vxl versus time. At FD ≤ 0.70, the disks are pinned, and Vxs = Vxl = 0 except for a brief sharp decay at very early times from a nonzero value. At intermediate FD values of 0.75, 0.8, and 0.85, the system is in phase II, where the density of the flowing disks remains homogeneous but some phase segregation occurs. Here we find large fluctuations in both Vxs and Vxl and, although the velocities of the two disk species are initially identical, as the system evolves the velocities separate so that at long times Vxs > Vxl. At FD/Fp=0.9, where phase III emerges and the small disks first segregate into a band, we can fit the velocity of the small disks to a stretched exponential form, as shown in Fig. 4(c) where we find Vxs ∝ e−t/τ with τ = 1.22 ×107. For comparison, we show a fit to Vxs ∝ tα with α = 0.26 ±0.01, which gives a poorer fit. We find a similar stretched exponential behavior at FD/Fp=0.95, and we show in Sec. III.C that this behavior is associated with enhanced transverse diffusion. The stretched exponential time response suggests that the formation of the segregated band of small disks is similar to an absorbing phase transition of the type found in clogging systems [37]. For FD/Fp = 1.0, 1.05, and 1.10, a stretched exponential fit gives a large time constant τ, and we show in Sec. III.C that these drives produce superdiffusion in the transverse direction. At higher driving forces FD > 1.10, the sample quickly reaches a steady flow phase IV state with constant Vxs and Vxl.

B.  High disk density

Fig5.png
Figure 5: Left panels: Large disk (blue circles) and small disk (red circles) positions for the system in Fig. 1 with Ψ = 1.4 and Ns=Nl. Center panels: nlloc (blue) and nsloc (red) as a function of y position. Right panels: ∆nloc as a function of y position. (a) ϕ = 0.58 and FD/Fp=0.5 in the driven homogeneous phase II. (b) ϕ = 0.70 and FD/Fp=0.5, showing the segregated liquid phase VI. (c) ϕ = 0.81 and FD/Fp=0.5, where we find an isotropic polycrystalline phase VII. (d) ϕ = 0.58 and FD/Fp=1.3, where the system fractionates into a liquid and smectic phase IV. (e) ϕ = 0.70 and FD/Fp=1.3, where the system is liquid throughout but forms distinct horizontal bands, giving a segregated phase VI. (f) ϕ = 0.81 and FD/Fp=1.3, which shows an isotropic polycrystalline phase VII similar to that found at lower drives.
When ϕ = 0.46, the effect of interstitial or unpinned disks on the depinning process becomes more important, and the depinning threshold drops to Fc/Fp = 0.5, as shown in Fig. 1. The peak in 〈Vxs〉 and 〈Vxl〉 at depinning is diminished in size, and we find that ∆〈Vx〉 ≈ 0.04 over the range 0.5 < FD/Fp < 1.0. At FD/Fp=0.5, illustrated in Fig. 5(a), ∆〈Vx〉 ≈ 0 and both types of disks are in a uniform phase II state containing small regions of higher disk density in the form of clumps and chains. For this drive, the plots of nlloc and nsloc in Fig. 5(a) indicate that each disk species is uniformly distributed across the sample. The corresponding velocity histogram P(vx) in Fig. 6(a) shows a bimodal distribution produced by the stick-slip motion of the disks, which are interacting strongly with the pinning sites. The vx=0 peak is higher than the vx=FD peak, indicating that the disks spend more time sticking and less time slipping, giving a low value of 〈Vx〉 in Fig. 1(a). At FD/Fp=1.3 in Fig. 5(d), where we again have ∆〈Vx〉 ≈ 0, the disks phase segregate into phase VI flow consisting of a liquid region surrounding a smectic region, which extends from 40 < y < 55. The smectic state is characterized by strongly asymmetric spacing of the disks, which are much closer together parallel to the drive than perpendicular to the drive. In this case, the smectic region contains mostly small disks and is of relatively low density. The density of the liquid region varies as a function of y, and the liquid is composed mainly of large disks separated by horizontal gaps for 10 < y < 30, while a densely packed liquid containing nearly equal numbers of small and large disks appears for y < 10. The large disks are almost completely depleted in the regions y ≈ 30 and 40 < y < 50 but have a nearly uniform density in the rest of the sample, as shown by the plot of nlloc in Fig. 5(d). In Fig. 6(d), P(vx) has a single peak at vx=FD=1.3 and a broad distribution of velocities in the range 0.3 ≤ vx ≤ 2.3, including a low velocity plateau.
For higher disk densities of ϕ = 0.58 to 0.87, Fc continues to decrease with increasing ϕ while ∆〈Vx〉 becomes small. The increased disk-disk interactions that occur at the higher densities not only diminish the depinning force, but also equalize the velocities of each disk species due to the higher frequency of disk-disk collisions. In Fig. 5(b), we show a ϕ = 0.70 sample at FD/Fp = 0.5 in phase VI, where the disks are in a liquid state containing some small localized clumps and chains. There is some species segregation, with the small disks preferentially located at the top of the sample and the large disks preferentially residing in the bottom of the sample, as indicated by the plots of nlloc and nsloc in Fig. 5(b). We find a bimodal distribution of P(vx) as shown in Fig. 6(b), but the two peaks are barely higher than the background plateau since the increased disk-disk interactions reduce the effectiveness of the pinning sites. The same sample at FD/Fp=1.3 remains in phase VI but develops polycrystalline structure in which the disks form wide species separated bands, as illustrated in Fig. 5(e). The polycrystalline clusters tend to be aligned in the driving direction. Figure 6(e) shows a single peak in P(vx) at vx=FD along with a broad distribution of velocities over the range 0.4 ≤ vx ≤ 2.4. The plateau at low vx has vanished since all of the disks are always moving at this drive, and it is replaced by a rapid decrease in P(vx) with decreasing vx.
At ϕ = 0.81, Fig. 5(c) shows that when FD/Fp=0.5, the disks have a combination of liquid like and polycrystalline structure in the isotropic polycrystalline phase VII. Although the plot of nsloc indicates that there is a local increase of small disk density near y ≈ 55, the disks are nearly jammed, and as a result further species segregation is suppressed. In Fig. 6(c), P(vx) has lost its distinct peaks and has a much more Gaussian shape, since the strong interactions between the disks prevent individual disks from being trapped by the pins. At FD/Fp=1.3 for the same sample in Fig. 5(f), phase VII flow is still present and the disk structure is nearly the same except that any slight tendency for segregation into a band has been destroyed. The plot of P(vx) in Fig. 6(f) shows a spread of velocities about vx=FD due to the tightly packed motion of the disks.
For densities of ϕ = 0.81 and above, the disks have a glassy arrangement at both low and high drives, and the high packing fraction inhibits rearrangements of the disks, preventing both species segregation and the realignment of the polycrystalline regions with the driving direction. We have tested the system for finite size effects using a larger sample with L=200, where we found structures similar to those illustrated in Figs. 2 and 5. The only difference is that the large system can accommodate multiple layers of segregated bands along the y direction.
Fig6.png
Figure 6: P(vx) for the small disks (red) and large disks (blue) for the system in Fig. 1 at (a) ϕ = 0.58 and FD/Fp=0.5 in phase II; (b) ϕ = 0.7 and FD/Fp=0.5 in phase VI; (c) ϕ = 0.81 and FD/Fp=0.5 in phase VII; (d) ϕ = 0.58 and FD/Fp=1.3 in phase IV; (e) ϕ = 0.7 and FD/Fp=1.3 in phase VI; (f) ϕ = 0.81 and FD/Fp=1.3 in phase VII.

C.  Transverse diffusion and topological order

Fig7.png
Figure 7: The transverse displacements 〈δys2〉 (red dashed line) and 〈δyl2〉 (blue dashed line) for the small and large disks obtained after 1×107 simulation time steps vs FD/Fp and the corresponding diffusive exponent αs (red squares) and αl (blue squares) for the system in Fig. 1 at ϕ = (a) 0.35, (b) 0.58, and (c) 0.70.
To further distinguish the phase behavior of each disk species, we measure the disk displacements in the direction transverse to the applied drive,
〈δys(l)2〉 = 1
Ns(l)
 Ns(l)
∑
i=1 
 [ yi(t) − yi(t0)]2,
(2)
for the small and large disks, respectively. We perform the measurement at intermediate times, after the system has had enough time to phase segregate. In Fig. 7 we plot 〈δys2〉 and 〈δyl2〉 obtained over the time interval 1×107 to 5×107 simulation time steps versus FD/Fp for samples with ϕ = 0.35, 0.58, and 0.7. We also show the corresponding diffusive exponents αs and αl obtained from long-time fits to 〈δys(l)2〉 ∝ tαs(l). At all densities, 〈δys(l)2〉 = 0 and αs(l)=0 for FD < Fc when the disks are motionless. Previous studies of monodisperse disks showed superdiffusive transverse flow with α > 1 in regimes where density phase separation occurred, since the increased frequency of disk-disk interactions in the high density region produces a greater amount of disk motion transverse to the driving direction [23]. The bidisperse disks have a more complex behavior since a wider variety of phase separated states occur that extend down to lower densities. In particular, the large and small disks generally exhibit different transverse diffusive behavior in the species separated regimes. We expect both the superdiffusive and subdiffusive regimes to cross over to regular diffusion at long time scales, where t >> 107.
In Fig. 7(a) at ϕ = 0.35, both disk species undergo subdiffusive transverse motion with αs(l) < 1 when FD > Fc. Transverse movement is suppressed at low disk density due to the infrequency of disk-disk collisions. Near FD/Fp=1.0 in phase III, we find large fluctuations of αs and αl due to the gradual emergence of the dense species separated bands illustrated in Fig. 2(b,c). Similar fluctuations in αs(l) appear in phase III near FD/Fp = 1 for 0.35 < ϕ < 0.5, where some samples reach a steady phase segregated, particle separated state within ∆t = 5 ×107 time steps while others do not. At FD/Fp=0.9 and 1.0 in the ϕ = 0.35 sample, the dense liquid band of small disks is surrounded by a homogeneous low density gas of large disks, and we find subdiffusive behavior with αs(l) < 1.0. Superdiffusive behavior with αs(l) > 1 appears at FD/Fp = 0.95 where the small disks have more fully segregated into a distinct horizontal band, and also at FD/Fp=1.05 and 1.1 where the small disks form a phase IV liquid-smectic low density state containing horizontal chains.
In Fig. 7(b) at ϕ = 0.58 we find diffusive transverse motion with αs(l) ≈ 1 whenever the disk density is homogeneous, including near depinning in phase II and for driving forces at which the phase VII densely packed polycrystalline regions appear. For drives just above depinning in phase II, both types of disk undergo superdiffusive transverse motion as the species separation illustrated in Fig. 5(a) occurs. The large disks transition to diffusive behavior at FD/Fp = 0.75 when phase III appears, while the small disks remain superdiffusive until FD/Fp = 1.3, where the system enters phase IV. Above FD/Fp = 1.3, the driving force dominates the disk motion and the transverse displacements are subdiffusive for both species. In Fig. 7(c) at ϕ = 0.70, the transverse motion is diffusive at depinning when FD = Fc. The large disks are superdiffusive in the range 0.3 < FD/Fp < 1.0, and become diffusive at higher drives. The small disks are diffusive in phase II for 0.3 < FD < 0.5, superdiffusive in phase VI for 0.5 < FD < 1.5, and diffusive above FD=1.5. A similar intermediate superdiffusive phase was observed in Ref. [42]. When the disk density is high, we find a transition from diffusive to subdiffusive behavior coinciding with the emergence of the locked polycrystalline phase VIII. For example, at ϕ = 0.814, αs(l) ≈ 1 for all FD > Fc. At ϕ = 0.87, αs(l) ≈ 0 since the disks are kinetically trapped.
Fig8.png
Figure 8: The average transverse nearest neighbor distance lnn vs FD/Fp for the system in Fig. 1 at ϕ = 0.06 (blue circles), 0.12 (blue triangles), 0.29 (blue squares), 0.35 (green stars), 0.58 (orange circles), 0.81 (red triangles), and 0.87 (brown pentagons).
To characterize lane formation, we measure 〈lnn〉, the average perpendicular distance between disks that are in contact, given by
〈lnn 〉 =   ⎛
√
〈Θ(rijdd−Rij)[Rij·
^
y
 
 ]2 〉
 
 ,
(3)
where Rij=Ri−Rj. In Fig. 8 we plot 〈lnn〉 versus FD/Fp for ϕ = 0.06 to ϕ = 0.87. For small disk densities in the range ϕ = 0.06 to 0.12, almost no disks are in contact with each other and 〈lnn 〉 is nearly zero. For higher disk densities, in the pinned phase I the disks tend to form blockages perpendicular to the drive that become more extensive as ϕ increases, giving larger values of 〈lnn〉. As the depinning threshold is approached, these blockages fall apart, so that 〈lnn 〉 decreases monotonically over the range 0 < FD < Fc. For ϕ = 0.29 and ϕ = 0.35, 〈lnn 〉 = 0 just below depinning where nearly all disk-disk contacts are lost, followed by a peak in 〈lnn 〉 near FD/Fp = 1 in phase III, where phase segregation into low and high density regions occurs. When phase IV chain structures form at higher FD, 〈lnn 〉 plateaus to a small but finite value. At ϕ = 0.58 and ϕ = 0.81, 〈lnn 〉 decreases steadily for FD > Fc, where Fc=0.4 and 0.2, respectively. At ϕ = 0.87, which is near the jamming limit, the system is always in phase VII above depinning and 〈lnn 〉 ≈ 0.6 over the entire range of FD/Fp shown in Fig. 8.
Fig9.png
Figure 9: (a) Heightfield plot of ∆〈Vx〉 as a function of total disk density ϕ vs driving force FD/Fp, based on the data in Fig. 1(c). Red (blue) indicates that the velocity of the small disks is higher (lower) than that of the large disks. (b) A schematic dynamic phase diagram as a function of ϕ vs FD/Fp. I: pinned or clogged; II: homogeneous density, with some species segregation; III: phase separated liquid-gas state; IV: phase separated liquid-smectic, or moving chain, state; V: homogeneous smectic or moving chain state; VI: segregated/banded liquid; VII: polycrystalline flowing state.
In Fig. 9 we show a heightfield plot of the ∆〈Vx〉 data from Fig. 1(c) as a function of disk density ϕ versus driving force FD/Fp for the Ψ = 1.4 system, while in Fig. 9(b) we present a schematic dynamic phase diagram as a function of ϕ vs FD/Fp. Phase I is the clogged or pinned state illustrated in Fig. 2(a). Phase II, consisting of homogeneous plastic flow with some species segregation, is shown in Fig. 5(a). Phase III is the density phase separated liquid/gas state from Fig. 2(b). Phase IV, a density phase separated liquid/smectic state, is illustrated in Figs. 2(c) and Fig. 5(d). Phase V is the moving smectic/chain state from Fig. 2(d). Phase VI, the moving segregated liquid, appears in Fig. 5(b,e), and phase VII is the moving polycrystalline state shown in Fig. 5(c) and (f). Except for phase VI, we do not distinguish fractionation by species within the phases. We note that the liquid-gas phase separation observed for monodisperse disks in Ref. [23] is different in character from what we find here. It occurs at higher disk densities of ϕ = 0.46 to 0.61 and is associated with the formation of close-packed clusters of disks.
The boundary between the pinned phase I and the moving phases II, V, or VII is determined by the critical depinning force plotted in Fig. 1(b). At low ϕ, where the pins outnumber the disks, the system depins directly into the moving smectic phase V. As ϕ increases, disk-disk interactions become important and the homogeneous phase II flow appears above depinning. For intermediate ϕ, this is followed at higher FD by density separation into the liquid/gas phase III or the liquid/smectic phase IV, while at higher drives the density becomes uniform again and the smectic phase V emerges. At higher ϕ, the disks are too dense to undergo phase separation and the system transitions directly from the homogeneous phase II flow to the banded solid phase VI. For very large disk densities, the disks can no longer exchange neighbors, and the system depins into a moving polycrystalline phase VII.

IV.  ENHANCED CRYSTALLIZATION AND BANDING WITH LARGER RADIUS RATIO AT Nl=Nd/2

We next increase the radius ratio to Ψ = 2.0, a value that is known to produce phase separation for disks driven out of equilibrium [26,28]. We fix Ns=Nl and consider disk densities in the range ϕ = 0.19 to 0.88, corresponding to ND/Np = 0.25 to 1.125. Here a disk density of ϕ = 0.78 corresponds to a ratio Np/ND = 1.0.
Fig10.png
Figure 10: (a) 〈Vxs〉 (solid lines) and 〈Vxl〉 (dashed lines) vs FD/Fp in a sample with Ψ = 2.0 and Ns=Nl at ϕ = 0.82 (down triangles), ϕ = 0.79 (pentagons), ϕ = 0.59 (right triangles), ϕ = 0.49 (stars), ϕ = 0.39 (squares), ϕ = 0.29 (up triangles), and ϕ = 0.20 (circles). (b) The corresponding d〈Vxs〉/dFD (solid lines) and d〈Vxl〉/dFD (dashed lines) vs FD/Fp curves for the same values of ϕ showing a peak near FD/Fp=1.0. Inset: Fc vs ϕ. (c) The corresponding ∆〈Vx〉 vs FD/Fp. Inset: a detail from the main panel of the region around FD/Fp=0.5 where ∆〈Vx〉 < 0 for large ϕ.
The plot of 〈Vxs〉 and 〈Vxl〉 versus FD/Fp in Fig. 10(a) for the Ψ = 2.0 system at different values of ϕ has similar behavior to that shown in Fig. 1(a), with a pinned phase I at low drives, a non-linear velocity-force relation above depinning, and a linear dependence of velocity on drive for high FD. The corresponding d〈Vxs〉/dFD and d〈Vxl〉/dFD versus FD/Fp curves in Fig. 10(b), as well as the plot of Fc versus FD/Fp in the inset of Fig. 10(b), are also similar to what was shown in Fig. 1(b). In Fig. 10(c), the plot of ∆〈Vx〉 versus FD/Fp indicates a higher velocity of the small disks at low ϕ similar to that found in Fig. 1(c); however, at low driving forces and high ϕ, we find that the large disks have a higher velocity than the small disks, as highlighted in the inset of Fig. 10(c).
At the lowest density of ϕ = 0.20 in Fig. 10, the small and large disks both have the same behavior, and the depinning occurs sharply at FD/Fp = 1.0, with a distinct transition from pinned to elastic flow of the homogeneous smectic phase V type. Since this system contains fewer disks than the Ψ = 1.4, ϕ = 0.23 system, the depinning transition is sharper, and the peak in d 〈Vxs 〉/d FD and d〈Vxl〉/ dFD at FD/Fp=1.0 is larger.
Fig11.png
Figure 11: Left panels: Large disk (blue circles) and small disk (red circles) positions for the system in Fig. 10 with Ψ = 2.0 and Ns=Nl. Center panels: nlloc (blue) and nsloc (red) as a function of y position. Right panels: ∆nloc as a function of y position. (a) ϕ = 0.29 and FD/Fp=0.95 in phase III segregated liquid/gas flow. (b) ϕ = 0.59 and FD/Fp=0.9 in phase VI segregated liquid flow. (c) ϕ = 0.79 and FD/Fp=0.9 in polycrystalline phase VII flow. (d) ϕ = 0.29 and FD/Fp=1.1 in phase IV liquid/smectic flow. (e) ϕ = 0.59 and FD/Fp=1.1 in phase VI segregated liquid flow. (f) ϕ = 0.79 and FD/Fp=1.1 in polycrystalline phase VII flow.
At ϕ = 0.29, we find an enhancement in the velocity of the small disks near depinning since the large disks can easily be pinned by traps and other large disks, while the small disks slip through smaller apertures to form a segregated dense band, as illustrated in Fig. 11(a) at FD/Fp=Fc=0.95. Here the large disks are uniformly distributed through the sample, while the small disks are concentrated in a band extending from 45 < y < 60. This is the same type of phase III segregation found in Fig. 2(b). In Fig. 10(b), d 〈Vxs 〉/d FD peaks at FD/Fp = 0.95, whereas d 〈Vxl 〉/d FD peaks at FD/Fp = 1.0, indicating that the smaller disks begin to flow freely at lower drives than the larger disks. Above FD/Fp = 1, there is a transition to phase IV flow consisting of a liquid of small disks surrounded by a smectic state of large disks, as illustrated in Fig. 11(d) for FD/Fp=1.1. This is accompanied by a large positive peak in ∆〈Vx〉 over the range 1.05 < FD/Fp < 1.25, as shown in Fig. 10(c). The smectic chain structure of the large disks increases the number of disk-disk interactions and diminishes the effectiveness of the pinning for the large disks. The small disks tend to form chains at higher drives.
Near depinning at ϕ = 0.39, we find a density phase segregated state containing distinct bands of high density liquid smectic regions and low density regions, similar to the phase III structure illustrated in Fig. 2(b). There are two distinct peaks in d〈Vxs〉/dFD and d〈Vxl〉/dFD in Fig. 10(b) near FD ≈ Fc = 0.75 where the small disks begin to move freely and FD ≈ Fp where the motion of the large disks increases. In Fig. 10(c), ∆〈Vx〉 > 0 over the range 0.8 < FD/FP < 1.0 in phase IV flow, indicating that the small disks can flow more easily in the liquid smectic region, which they preferentially occupy. At ϕ = 0.49, there is a pronounced crossover in ∆〈Vx 〉 in Fig. 10(c) from a negative value for 0.6 < FD/Fp < 0.7 to a positive value for 0.8 < FD/Fp < 1.0, indicating that the large disks are moving faster than the small disks at lower drives but slower at higher drives.
For ϕ = 0.59, ∆〈Vx〉 is never positive but has an enhanced negative region at low drives above depinning in the range 0.4 < FD/Fp < 0.9, as highlighted in the inset of Fig. 10(c). Species segregation of the disks into phase VI flow occurs in the window 0.8 < FD/Fp < 0.9. As illustrated in Fig. 11(b) for FD/Fp=0.9, the large disks form a cluster that spans nearly the entire system, while the small disks are concentrated in a band ranging from 20 < y < 40. The small disks form relatively few disk-disk contacts, making them less likely to be depinned due to disk-disk interactions, and thus reducing their velocity compared to the large disks. At higher drives, all of the disks depin and the difference in velocity among the two disk species drops to zero. At FD=1.1, shown in Fig. 11(e), we find phase VI flow where the small disks remain in a single high density band while the large disks form a low density smectic state at 0 < y < 10 coexisting with a high density liquid state containing polycrystalline regions at 35 < y < 60. A low density void region appears at 10 < y < 20. The motion of the particles in this state is illustrated in the Supplementary Material [43].
When ϕ ≥ 0.59, d〈Vxs 〉/FD and d〈Vxl 〉/FD have a smooth rather than sharp increase at FD = Fc. There is an extended regime in which the velocity of the large disks is higher than that of the small disks, with ∆〈Vx〉 < 0 over the range 0.2 < FD/Fp < 1.5 for the ϕ = 0.79 system. As shown in Fig. 11(c) for ϕ = 0.79 at FD/Fp=0.9, a significant fraction of the large disks form tight polycrystalline packings while the small disks form trapped clusters over specific horizontal windows. This phase VII structure remains similar at higher drives, as shown in Fig. 11(e) at FD/Fp=1.1. For larger systems with L=200 at high ϕ, we find multiple large polycrystalline regions rather than a single band spanning the system.

  Transverse diffusion and topological order

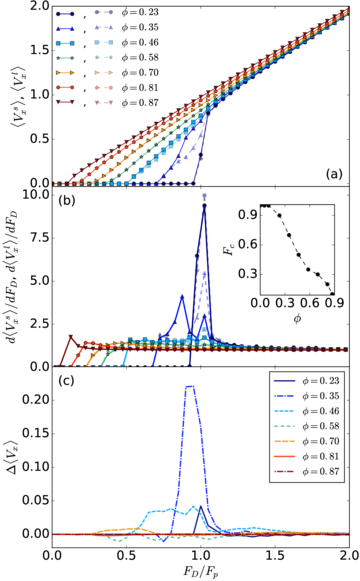
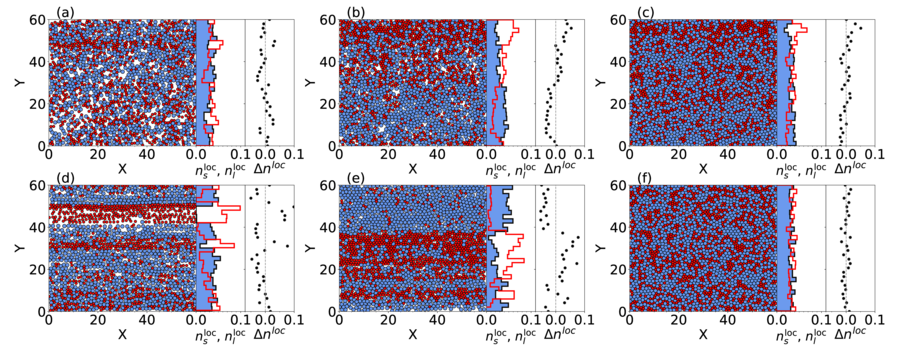
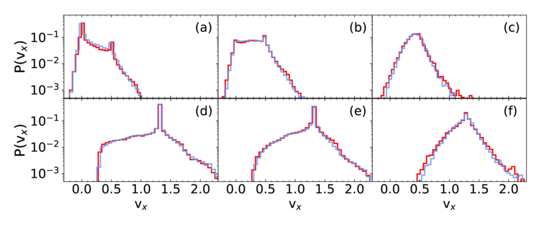
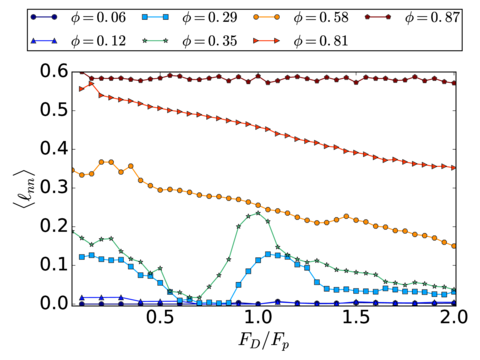
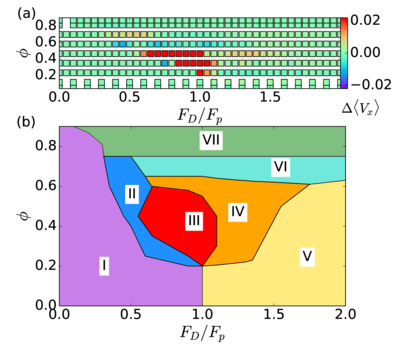
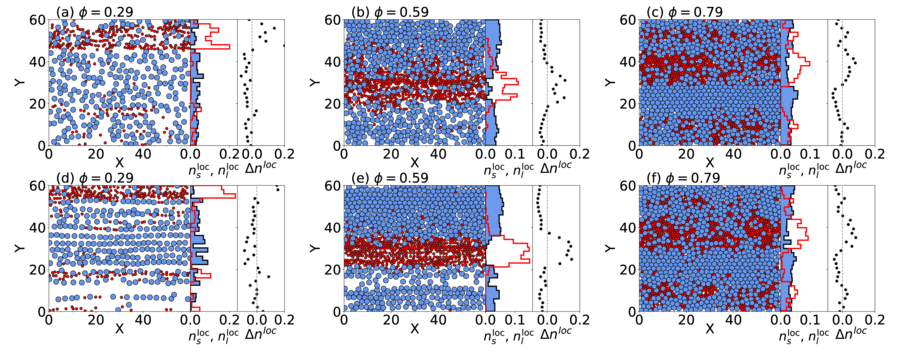
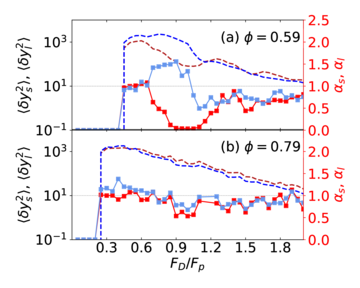
Fig12.png
Figure 12: Transverse displacements 〈δys2〉 (red dashed line) and 〈δyl2〉 (blue dashed line) for the small and large disks obtained after 1 ×107 simulation time steps vs FD/Fp and the corresponding diffusive exponent αs (red squares) and αl (blue squares) for the system in Fig. 10 with Ψ = 2.0 for densities ϕ = (a) 0.59 and (b) 0.79.
In Fig. 12, we plot the transverse diffusion 〈δys2 〉 and 〈δyl2〉 along with the exponents αs and αl versus FD/Fp for the Ψ = 2.0 system from Fig. 10. At ϕ = 0.59 in Fig. 12(a), we find homogeneous phase II flow with αs ≈ αl ≈ 1 at low driving forces of 0.4 < FD/Fp < 0.6, indicating diffusive behavior. At intermediate driving forces, 0.6 < FD/Fp < 1.2, phase VI flow appears and the small disks are subdiffusive since they have become confined in a horizontal band, as shown in Fig. 11(b) and (e). The large disks are superdiffusive for 0.6 < FD/Fp < 1.0, and become subdiffusive at higher drives once their structure changes from a homogeneous liquid with small voids to a denser liquid containing a large horizontal gap. The small voids permit a transverse flow of the large disks that is suppressed once a large void opens at higher drives. For 1.2 < FD/Fp < 2.0, the driving force dominates the behavior of both disk species, which form chain states that move subdiffusively in the transverse direction. At ϕ = 0.79 in Fig. 12(b), the system is in phase VII flow and αs ≈ αl ≈ 1 at all driving forces above depinning, indicating diffusive transverse flow for both disk species. This is expected in a liquid phase containing polycrystalline regions of homogeneous density.
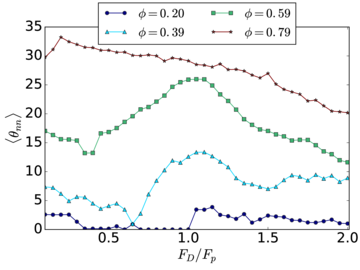
Fig13.png
Figure 13: 〈θnn 〉 vs FD/Fp for the system in Fig. 10 with Ψ = 2.0 for ϕ = 0.20 (circles), 0.39 (triangles), 0.59 (squares), and 0.79 (stars).
In Fig. 13, we characterize the lane structure of the disks based on the average angle between disks that are in contact,
〈θnn 〉 = 1
Nd
 Nd
∑
i 
 Θ(rijdd−Rij) tan−1⎛
⎜
⎝ 		⎢
⎢
⎢
Rij·
^
y
 
Rij ·
^
x
 
⎢
⎢
⎢ 		⎞
⎟
⎠ 		,
(4)
sampled every ∆t = 5 ×105 simulation time steps after the system has reached a steady state. This measure is closely related to 〈lnn 〉 from Fig. 8. Figure 13 shows 〈θnn〉 versus FD/Fp for systems with ϕ = 0.2, 0.39, 0.59, and 0.79. For ϕ = 0.20, 〈θnn 〉 is low for all drives due to the phase V smectic flow which favors disk-disk contacts that are aligned with the x direction. We find 〈θnn 〉 ≈ 30° near depinning for ϕ = 0.79, since the polycrystalline disk arrangements in phase VII tend to contain crystallites aligned with the x axis that contribute angles of 0° and 60° equally to the sum. As the driving force increases, 〈θnn〉 decreases monotonically due to an increase in the amount of smectic or chainlike ordering in the system. For ϕ = 0.39 and ϕ = 0.59, a local maximum in 〈θnn〉 at FD/Fp = 1 is produced by the denser structures that form in the phase VI flow when the phase separation is maximized for nearly equal pinning and driving strengths. This is followed by a decrease in 〈θnn〉 at higher drives as smectic ordering emerges.
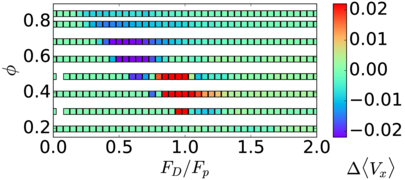
Fig14.png
Figure 14: Heightfield plot of ∆〈Vx〉 as a function of total disk density ϕ vs driving force FD/Fp, based on the data in Fig. 10(c). Red (blue) indicates that the velocity of the small disks is higher (lower) than that of the large disks. We find a large region in which ∆〈Vx〉 < 0.
In Fig. 14, we show a heightfield plot of ∆〈Vx〉 as a function of ϕ versus FD/Fp for the Ψ = 2.0 system. Compared to the Ψ = 1.4 system in Fig. 9, we find a much larger region in which ∆〈Vx 〉 < 0. This indicates that increasing the relative size of the large disks can also increase their velocity relative to the small disks when the driving force is close to the depinning threshold and the total disk density is sufficiently large.

V.  LOWER FRACTION OF LARGE DISKS, Nl=Nd/10

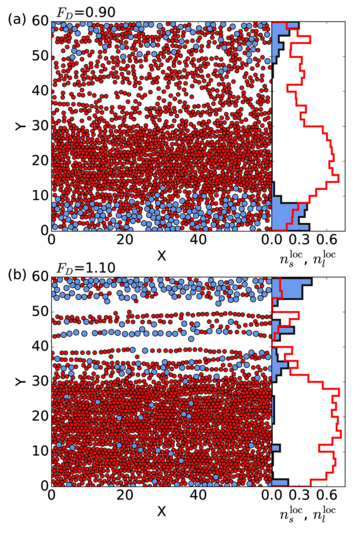
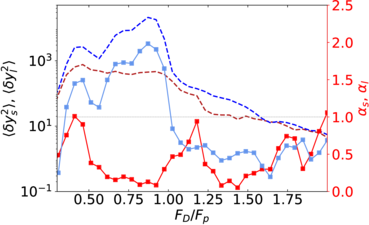
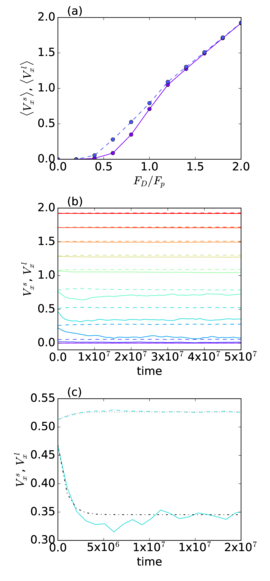
Fig15.png
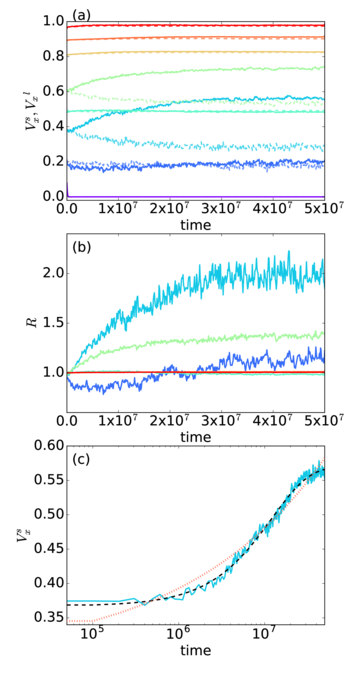
Figure 15: (a) 〈Vxs〉 (solid lines) and 〈Vxl〉 (dashed lines) vs FD/Fp in a sample with Ψ = 1.4, Ns=0.9Nd, and Nl=0.1Nd at ϕ = 0.48. (b) The instantaneous disk velocity Vxs (solid lines) and Vxl (dashed lines) versus time for the small and large disks, respectively, in the sample from panel (a) at FD=0.2 (phase I), 0.4, 0.6, 0.8 (phase IIIa), 1.0, 1.2 (phase IVa), 1.4, 1.6, 1.8, and 2.0 (phase V), from bottom to top. The large disks reach a steady state quickly, while the small disks continue to evolve at t > 107 timesteps. (c) A detail showing only the FD=0.8 curves in phase IIIa from panel (b). Dot-dashed line: A fit to 〈Vxs〉 = et/τs with τs=8.46 ×105. Dotted line: A fit to 〈Vxl〉 = et/τl with τl=1.19 ×106.
Fig16.png
Figure 16: Left panels: Large disk (blue circles) and small disk (red circles) positions for the system in Fig. 15 with Ψ = 1.4 and Nl=0.1Nd at ϕ = 0.48. Right panels: nlloc (blue) and nsloc (red) as a function of y position. (a) FD/Fp=0.9 in phase IIIa flow. (b) FD/Fp=1.1 in phase IVa flow.
Fig17.png
Figure 17: Transverse displacements 〈δys2〉 (red dashed line) and 〈δyl2〉 (blue dashed line) for the small and large disks obtained after 1 ×107 simulation time steps vs FD/Fp and the corresponding diffusive exponent αs (red squares) and αl (blue squares) for the system in Fig. 15 with Ψ = 1.4 and Nl=0.1Nd at ϕ = 0.48.
We next investigate the effect of changing the disk species ratio from Ns=Nl=0.5Nd to Ns=0.9Nd and Nl=0.1Nd for a system with Ψ = 1.4. We find the same general phases as described in Sec. III but with a greater tendency for the large disks to move faster than the small disks. In Fig. 15(a), we plot 〈Vxs〉 and 〈Vxl〉 versus FD/Fp for the Nl=0.1Nd system at a disk density of ϕ = 0.48. We find plastic depinning for both disk species, as indicated by the concave shape of the velocity-force curve, followed by a transition at higher drives to a linear dependence. At FD/Fp=0.9, illustrated in Fig. 16(a), the system can be divided into three regions: a small disk liquid, a small disk gas, and a mixed gas-like region containing both disk species at an intermediate density. We label this state phase IIIa flow. At a higher drive of FD/Fp=1.1 in Fig. 16(b), the small disk liquid has increased in density and contains a few large disks. In this phase IVa flow, a window of large disk liquid containing some small disks runs along one side of the small disk liquid, while the low density region of the sample contains roughly equal numbers of small and large disks arranged in a smectic structure. Due to the strong species segregation, these phases resemble the states found for monodisperse disks in Ref. [23]. Over the range 0.2 < FD/Fp < 1.6 where the species separation occurs, 〈Vxl 〉 > 〈Vxs 〉, giving ∆〈Vx〉 < 0 (not shown).
In Fig. 15(b), we plot the time evolution of 〈Vxs 〉 and 〈Vxl〉 for the same ϕ = 0.48 system at FD values ranging from FD/Fp=0.2 to FD/Fp=2.0. For FD/Fp ≤ 0.2, the system is in the pinned phase I and 〈Vxs 〉 = 〈Vxl〉 = 0. When FD/Fp ≥ 0.4, phase IIIa flow appears and we find 〈Vxl 〉 > 〈Vxs 〉, with 〈Vxl〉 remaining nearly constant over time while 〈Vxs〉 decays. For intermediate driving forces of 0.6 < FD/Fp < 1.2, extending through the regime of phase IV flow, the 〈Vxs〉 curves have an exponential shape, 〈Vxs 〉 ∝ e−t/τs + 〈Vo 〉, as shown in Fig. 15(c) for FD / Fp = 0.8, where τs = 8.46 ×105. A similar fit of 〈Vxl〉 at the same drive gives a time constant τl = 1.19 ×106 that is somewhat larger. As FD/Fp increases above 1.2, the system rapidly reaches a phase V steady state and the difference between the velocity of the small and large disks vanishes. Due to the lengthy transient dynamics at intermediate FD/Fp, we wait a minimum of 2 ×107 simulation time steps before measuring the velocity-force curves shown in Fig. 15(a).
In Fig. 17 we plot the transverse displacements 〈δys2 〉 and 〈δyl2〉 versus FD/Fp for the ϕ = 0.48 sample along with the corresponding exponents αs and αl. All four quantities increase monotonically between FD = Fc and FD/Fp = 0.4. At intermediate FD, in phase IIIa, we find subdiffusive transverse motion of the small disks with αs < 1 accompanied by superdiffusive transverse motion of the large disks with αl > 1. Here the small disks are confined within a dense liquid, while the large disks are in a low density region in which interactions with pinning sites can enhance the transverse diffusion. At large FD where phase V smectic structures emerge, both disk species have subdiffusive transverse motion.

VI.  SCALING NEAR THE DEPINNING TRANSITION

In systems of particles that have long range interactions, the velocity-force relationship scales as V ∝ (FD − Fc)−β near depinning [1]. For elastic depinning in which the structure of the particle lattice remains unchanged, β = 2/3, while when the depinning transition is plastic, β > 1.0. For Coulomb [8] and screened Coulomb [15,44] interaction potentials, the plastic depinning exponents are β ≈ 1.65 and 2.0, respectively, while simulations of depinning of superconducting vortices with a Bessel function vortex-vortex interaction give β = 1.3[44]. It is interesting to ask whether similar scaling of the velocity-force curves occurs in the disk system. For monodisperse disks with Np / Nd > 0.288, it was shown in Ref. [23] that the velocity-force curves can be fit to a power law with 1.4 < β < 1.7.
Fig18.png
Figure 18: 〈Vxs〉 (solid lines) and 〈Vxl〉 (dashed lines) vs FD−Fc on a log-log scale for the sample from Fig. 1 with Ψ = 1.4 and Ns=Nl. We fit the data to 〈Vxs(l)〉 ∝ (FD−Fc)−β (pink lines). (a) ϕ = 0.46 with β = 1.0. (b) ϕ = 0.58 with β = 1.3.
In Fig. 18(a,b) we plot 〈Vxs 〉 and 〈Vxl〉 versus FD − Fc on a log-log scale at densities of ϕ = 0.46 and 0.58, respectively. By fitting the portion of the curve closest to depinning, we find 1.0 < β < 1.3. The scaling fit can be performed only for ϕ > 0.35 and does not work at low disk densities. We find similar scaling fits for sufficiently large disk densities for the Ψ = 2.0 system and for the Ψ = 1.4 and Nl=0.1Nd system. The depinning is clearly not elastic, but the lower values of β compared to systems with longer range interactions suggest that the type of plastic depinning that occurs may be different for short range interacting systems than for longer range interacting systems.

VII.  CONTINUOUS DRIVING FORCE

In the results presented above, we performed individual simulations for each value of FD starting from a uniform initial disk configuration in each simulation. To check whether cumulative disk rearrangements affect the velocity response and ordering, and also to test for the presence of hysteresis, we next consider a set of simulations in which we continuously sweep FD up a series of steps with increment size ∆FD=0.05. We increase FD from FD=0 to FD=2.0, and then continuously decrease FD with ∆FD=−0.05 from FD=2.0 back down to FD=0, spending 5 ×107 simulation time steps at each drive increment in order to let the system reach a steady state. We apply this continuous sweep protocol to systems with Ψ = 1.4 and ϕs=ϕl at two densities, ϕ = 0.35 and ϕ = 0.46, and compare it to the discrete ramp protocol.
Fig19.png
Figure 19: (a) 〈Vxs〉 and 〈Vxl〉 vs FD/Fp for a continuous ramp in a system with with ϕ = 0.35, Ψ = 1.4 and Ns=Nl. Solid lines: upward sweep of FD; dashed lines: downward sweep of FD. (b) 〈CL〉 vs FD/Fp. Solid lines: upward sweep of FD; dashed lines: downward sweep of FD.
Fig20.png
Figure 20: (a) 〈Vxs〉 and 〈Vxl〉 vs FD/Fp for a continuous ramp in a system with ϕ = 0.46, Ψ = 1.4 and Ns=Nl. Solid lines: upward sweep of FD; dashed lines: downward sweep of FD. (b) 〈CL〉 vs FD/Fp. Solid lines: upward sweep of FD; dashed lines: downward sweep of FD.
In Fig. 19(a) we plot 〈Vxs〉 and 〈Vxl〉 for the upward and downward sweeps in the ϕ = 0.35 system, and in Fig. 20(a) we show the same quantities for the ϕ = 0.46 sample. In each case we find no velocity hysteresis. The ϕ = 0.35 system undergoes phase segregation but does not show the disk species separation found with the discrete ramp protocol. In the ϕ = 0.46 system, both phase segregation and disk species separation occur.
We also measure the average largest cluster size of the system, 〈CL〉, versus FD/Fp, as shown in Fig. 19(b) for ϕ = 0.35 and Fig. 20(b) for ϕ = 0.46. To determine CL, we use the cluster counting algorithm of Luding and Herrmann [45] to identify clusters of disks that are all touching each other, and we then record the size of the largest cluster in the system. We then average this quantity over time to obtain 〈CL〉. Hysteresis appears in 〈CL〉 within the pinned phase I. As the drive increases from FD=0, large clusters form as disks become trapped and prevent interstitial disks from flowing, and the value of 〈CL〉 is relatively high just below the depinning transition. In the ϕ = 0.35 sample, once the disks depin the clusters break apart, giving a gradual decrease in 〈CL〉 with increasing FD, but once the system enters the phase IV regime near FD/Fp=1.1, the disks form chain structures that are nearly the same size as the clusters that formed below depinning, so 〈CL〉 stabilizes and then increases slightly with increasing FD as the chain length gradually increases. In the ϕ = 0.46 sample, there is also a drop in 〈CL〉 above depinning as the clusters dissolve, but the chains that form in phase IV are relatively short, so 〈CL〉 saturates at a steady low value. Upon reversing the drive, the evolution of 〈CL〉 is not hysteretic until the sample repins and the evolution of the disk structures is frozen. Since the disks have already rearranged during the upward sweep of the drive, there are no disk rearrangements below the repinning transition and 〈CL〉 remains fixed at a value lower than that which appears on the upward ramp when pinned clusters of disks are slowly evolving.

VIII.  DISCUSSION

Our work suggests that dynamical phase separation, particle species segregation, and laning effects are general features of driven systems with short range hard disk particle-particle interactions moving over random disorder. Observing these results experimentally requires access to a sample in the overdamped limit where thermal fluctuations are absent, such as colloidal particles suspended in a viscous fluid or colloidal particles of relatively large size for which thermal effects are small [46,47]. Additionally, in certain superconducting vortex systems, multiple vortex species could be stable and the vortex-vortex interactions would be effectively short range near phase boundaries [48]. Other systems include magnetic bubbles with different bubble sizes [49], multi-species skyrmions [50,51], and emulsions composed of binary species [52]. Our results could have some relevance to granular matter; however, our model does not include inertial terms or frictional interactions, both of which are often important in granular systems. One possible similar system would be granular matter suspended in fluid moving over a random surface.
The unusual phase separated states observed in the bidisperse hard disk system arise at certain disk densities and driving forces and result from a velocity collapse mechanism that occurs whenever the mobility becomes density dependent such that an isolated disk can move more rapidly than disks within a cluster. The resulting voids in the sample have no energy penalty due to the short range of the disk-disk interaction potential. Similar clustering appears in a system of monodisperse disks [24].
We measure only the transverse diffusion of the disks since the driving force induces ballistic motion in the longitudinal direction, similar to that which appears for active matter. The net motion is therefore generally superdiffusive over extended time scales, as described in Section III +.1667emC. Even though the behavior becomes diffusive at the longest time scales, it is still superdiffusive on the time scale of collective interactions.
Our simulations could be extended to include thermal fluctuations, finite inertia, and/or different disk-disk interaction potentials. We expect that the clustering of the disks would break down under increasing temperature, which would tend to homogenize the disk density; however, species phase segregation may still occur for entropic reasons. Introduction of an inertial term to the equations of motion would produce more Gaussian-like fluctuations of the motion of the disks, unlike the nonequilibrium fluctuations produced by the external applied driving force, and should change the nature of the dynamical states. It would be interesting to study a system of soft interacting disks that can strongly overlap, such as an experimental bubble array system [14]. In this foam or bubble limit, it may be possible to obtain states in which some particles are pinned while other particles are able to squeeze past the pinned particles. This system could access densities above the hard sphere jamming density, where stress fields and other long range effects would become important.

IX.  SUMMARY

We examine the dynamics of bidisperse disks driven over random quenched disorder to explore the dynamical phases of particles with short range interaction forces. At low disk densities, we observe a pinned state that transitions into a strongly chained state where the disks can undergo local demixing but where the overall disk distribution is homogeneous. At intermediate disk densities, the disks depin into a disordered flow state exhibiting stick slip dynamics, followed by a species segregated state in which the small disks form clusters and the large disks remain evenly distributed throughout the sample. For intermediate drives the disks form a partially laned state exhibiting both species separation and density segregation, while at high drives a mixed laning state emerges. At high disk densities of ϕ > 0.75, a rigid polycrystalline state appears that moves as a solid and undergoes no species or density segregation. Both the density and the species segregation effects are the most prominent near FD=Fp when the driving force and pinning force directly compete. The anisotropic fluctuations induced by the pinning at high drives favor the formation of laned states. It is also possible to induce mixing between the two species just above the depinning transition. By increasing the radius of the large disks compared to that of the small disks, we find a larger amount of crystallization and banding of the large disks, while the small disks tend to form an interstitial liquid. Lowering the fraction of large disks compared to the fraction of small disks tends to increase the velocity of the large disks compared to that of the small disks, which species separate into a disordered liquid that flows unevenly over the pinning sites. When the disk density is sufficiently large, we find scaling of the velocity-force curves near the plastic depinning transition with an exponent that is slightly smaller than what is observed in systems with longer range interparticle interactions, suggesting that the plastic depinning transition may have distinct features when the interaction range is very short.
Our results could be relevant to multi-species flows of soft matter through random substrates or the flow of granular matter over a disordered background. It would be interesting to explore possible segregation effects for bidisperse systems with long range particle-particle interactions driven over random disorder. In the disk system, the segregation of particles into clumps reduces the number of disk-disk collisions and enhances the disk flow.

ACKNOWLEDGMENTS

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396. This research was supported in part by the University of Notre Dame Center for Research Computing and the Wabash College Computational Chemistry Cluster.

REFERENCES

[1]
C. Reichhardt and C.J.O. Reichhardt, Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: a review, Rep. Prog. Phys. 80, 026501 (2017).
[2]
S. Bhattacharya and M. J. Higgins, Dynamics of a disordered flux line lattice, Phys. Rev. Lett. 70, 2617 (1993).
[3]
A. E. Koshelev and V. M. Vinokur, Dynamic melting of the vortex lattice, Phys. Rev. Lett. 73, 3580 (1994).
[4]
M. C. Faleski, M. C. Marchetti, and A. A. Middleton, Vortex dynamics and defects in simulated flux flow, Phys. Rev. B 54, 12427 (1996).
[5]
F. Pardo, F. de la Cruz, P.L. Gammel, E. Bucher, and D.J. Bishop, Observation of smectic and moving-Bragg-glass phases in flowing vortex lattices, Nature (London) 396, 348 (1998).
[6]
C.J. Olson, C. Reichhardt, and F. Nori, Nonequilibrium dynamic phase diagram for vortex lattices, Phys. Rev. Lett. 81, 3757 (1998).
[7]
M.-C. Cha and H. A. Fertig, Topological defects, orientational order, and depinning of the electron solid in a random potential, Phys. Rev. B 50, 14368 (1994).
[8]
C. Reichhardt, C. J. Olson, N. Grønbech-Jensen, and F. Nori, Moving Wigner glasses and smectics: Dynamics of disordered Wigner crystals, Phys. Rev. Lett. 86, 4354 (2001).
[9]
T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, and A. Rosch, Emergent electrodynamics of skyrmions in a chiral magnet, Nature Phys. 8, 301 (2012).
[10]
C. Reichhardt, D. Ray, and C. J. Olson Reichhardt, Collective transport properties of driven skyrmions with random disorder, Phys. Rev. Lett. 114, 217202 (2015).
[11]
W. Koshibae and N. Nagaosa, Theory of current-driven skyrmions in disordered magnets, Sci. Rep. 8, 6328 (2018).
[12]
C. Reichhardt, C.J.O. Reichhardt, I. Martin, and A.R. Bishop, Dynamical ordering of driven stripe phases in quenched disorder, Phys. Rev. Lett. 90, 026401 (2003).
[13]
H.J. Zhao, V.R. Misko, and F. M. Peeters, Dynamics of self-organized driven particles with competing range interaction, Phys. Rev. E 88, 022914 (2013).
[14]
J. Hu and R.M. Westervelt, Collective transport in two-dimensional magnetic bubble arrays, Phys. Rev. B 51, 17279(R) (1995).
[15]
C. Reichhardt and C. J. Olson, Colloidal dynamics on disordered substrates, Phys. Rev. Lett. 89, 078301 (2002).
[16]
A. Pertsinidis and X.S. Ling, Statics and dynamics of 2D colloidal crystals in a random pinning potential, Phys. Rev. Lett. 100, 028303 (2008).
[17]
S. Deutschländer, T. Horn, H. Löwen, G. Maret, and P. Keim, Two-dimensional melting under quenched disorder, Phys. Rev. Lett. 111, 098301 (2013).
[18]
Y.G. Cao, Q.X. Li, G.Y. Fu, J. Liu, H.Z. Guo, X. Hu, and X.J. Li, Depinning dynamics of two-dimensional magnetized colloids on a random substrate, J. Phys.: Condens. Matter 22, 155101 (2010).
[19]
P. Tierno, Depinning and collective dynamics of magnetically driven colloidal monolayers, Phys. Rev. Lett. 109, 198304 (2012).
[20]
C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, Active Brownian particles in complex and crowded environments, Rev. Mod. Phys. 88, 045006 (2016).
[21]
A. Morin, N. Desreumaux, J.-B. Caussin, and D. Bartolo, Distortion and destruction of colloidal flocks in disordered environments, Nat. Phys. 13, 63 (2017).
[22]
Cs. Sándor, A. Libál, C. Reichhardt, and C.J.O. Reichhardt, Dynamic phases of active matter systems with quenched disorder, Phys. Rev. E 95, 032606 (2017).
[23]
Y. Yang, D. McDermott, C.J.O. Reichhardt, and C. Reichhardt, Dynamic phases, clustering, and lane formation for driven disk systems in the presence of quenched disorder, Phys. Rev. E 95, 042902 (2017).
[24]
C. Reichhardt and C.J.O. Reichhardt, Aspects of jamming in two-dimensional athermal frictionless systems, Soft Matter 10, 2932 (2014).
[25]
C.S. O'Hern, L.E. Silbert, A.J. Liu, and S. R. Nagel, Jamming at zero temperature and zero applied stress: The epitome of disorder, Phys. Rev. E 68, 011306 (2003).
[26]
K.M. Hill and J. Kakalios, Reversible axial segregation of binary mixtures of granular materials, Phys. Rev. E 49, R3610(R), (1994).
[27]
S.B. Santra, S. Schwarzer, and H. Herrmann, Fluid-induced particle-size segregation in sheared granular assemblies, Phys. Rev. E 54, 5066 (1996).
[28]
A. Samadani, and A. Kudrolli, Segregation transitions in wet granular matter, Phys. Rev. Lett. 85, 5102 (2000).
[29]
S.J. Fiedor, and J.M. Ottino, Dynamics of axial segregation and coarsening of dry granular materials and slurries in circular and square tubes, Phys. Rev. Lett. 91, 244301 (2003).
[30]
J. Dzubiella, G.P. Hoffmann, and H. Löwen, Lane formation in colloidal mixtures driven by an external field, Phys. Rev. E 65, 021402 (2002).
[31]
I.S. Santos de Oliveira, W.K. den Otter, and W. J. Briels, Alignment and segregation of bidisperse colloids in a shear-thinning viscoelastic fluid under shear flow, Eur. Phys. Lett. 101, 2802 (2013).
[32]
C. Reichhardt, and C.J.O. Reichhardt, Velocity force curves, laning, and jamming for oppositely driven disk systems, Soft Matter 14, 490 (2018).
[33]
C.J.O. Reichhardt, E. Groopman, Z. Nussinov, and C. Reichhardt, Jamming in systems with quenched disorder, Phys. Rev. E 86, 061301 (2012).
[34]
See supplemental material at http://link.aps.org/supplemental/10.1103/PhysRevE.99.042601. See Fig3b.mp4 for the disk dynamics at ϕ = 0.35 and FD/Fp=0.9.
[35]
See supplemental material at http://link.aps.org/supplemental/10.1103/PhysRevE.99.042601. See Fig3c.mp4 for the disk dynamics at ϕ = 0.35 and FD/Fp = 1.1.
[36]
See supplemental material at http://link.aps.org/supplemental/10.1103/PhysRevE.99.042601. See Fig3d.mp4 for the disk dynamics at ϕ = 0.35 and FD/Fp = 2.0.
[37]
H. Peter, A. Libal, C. Reichhardt, and C.J.O. Reichhardt, Crossover from jamming to clogging behaviors in heterogeneous environments, Sci. Rep. 8, 10252 (2018).
[38]
P. Le Doussal and T. Giamarchi, Moving glass theory of driven lattices with disorder, Phys. Rev. B 57, 11356 (1998).
[39]
L. Balents, M.C. Marchetti, and L. Radzihovsky, Nonequilibrium steady states of driven periodic media, Phys. Rev. B 57, 7705 (1998).
[40]
K. Moon, R. T. Scalettar, and G. T. Zimányi, Dynamical phases of driven vortex systems, Phys. Rev. Lett. 77, 2778 (1996).
[41]
A. Kolton, D. Domínguez, and N. Grønbech-Jensen, Hall noise and transverse freezing in driven vortex lattices, Phys. Rev. Lett. 83, 3061 (1999).
[42]
C. Heussinger, L. Berthier, and J.-L. Barrat, Superdiffusive, heterogeneous, and collective particle motion near the fluid-solid transition in athermal disordered materials, EPL 90, 20005 (2010).
[43]
See supplemental material at http://link.aps.org/supplemental/10.1103/PhysRevE.99.042601. See Fig11e.mp4 for the disk dynamics at Ψ = 2.0, ϕ = 0.59 and FD/Fp = 1.1.
[44]
Y. Fily, E. Olive, N. Di Scala, and J. C. Soret, Critical behavior of plastic depinning of vortex lattices in two dimensions: Molecular dynamics simulations, Phys. Rev. B 82, 134519 (2010).
[45]
S. Luding and H.J. Herrmann, Cluster-growth in freely cooling granular media, Chaos 9, 673 (1999).
[46]
D.J. Pine, J. P. Gollub, J. F. Brady, and A.M. Leshansky, Chaos and threshold for irreversibility in sheared suspensions, Nature (London) 438, 997 (2005).
[47]
R.L. Stoop and P. Tierno, Clogging and jamming of colloidal monolayers driven across disordered landscapes, Commun. Phys. 1, 68 (2018).
[48]
C. Reichhardt, G.T. Zimányi, R.T. Scalettar, A. Hoffmann, and I.K. Schuller, Individual and multiple vortex pinning in systems with periodic pinning arrays, Phys. Rev. B 64, 052503 (2001).
[49]
R. Seshadri, and R. M. Westervelt, Statistical mechanics of magnetic bubble arrays. I. Topology and thermalization, Phys. Rev. B 46, 5142, (1992).
[50]
W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F. Y. Fradin, J. E. Pearson, Y. Tserkovnyak, K. L. Wang, O. Heinonen, S. G. E. te Velthuis, A. Hoffmann, Blowing magnetic skyrmion bubbles, Science 349, 283 (2015).
[51]
C.J.O. Reichhardt and C. Reichhardt, Disordering, clustering, and laning transitions in particle systems with dispersion in the Magnus term, Phys. Rev. E 99, 012606 (2019).
[52]
M.E. Cates and E. Tjhung, Theories of binary fluid mixtures: from phase-separation kinetics to active emulsions, J. Fluid Mech. 836, 1 (2018).


File translated from TEX by TTHgold, version 4.00.
 Back to Home