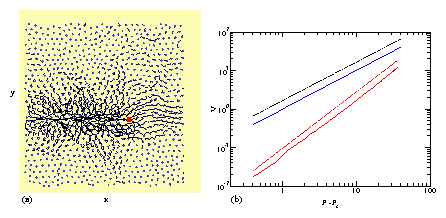
 Fig. 6:
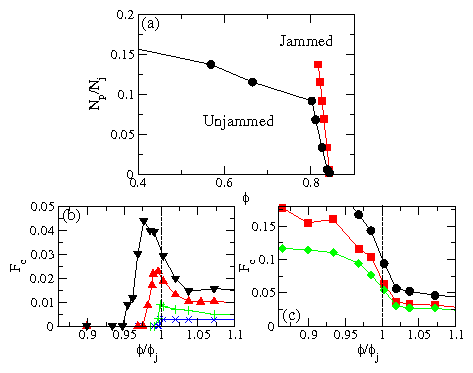
Jamming in a system of bidisperse disks driven through an obstacle array.
(a) Jamming diagram for Np/Nj vs ϕ.
Np is the number of obstacles and Nj is the number of disks in an
obstacle-free system at the jamming density.
ϕ is the disk density.
The system is defined to be jammed when the disks do not
continuously move under an arbitrarily small
applied drift force.
Jammed states exist above and to the right of the black line, and unjammed
states are found below the black line.
The red squares indicate the value of ϕ above which the particles
flow as a solid. Near point J, the jamming density decreases linearly with
increasing Np/Nj, while for ϕ < 0.8, the line separating the
jammed and unjammed states is much flatter.
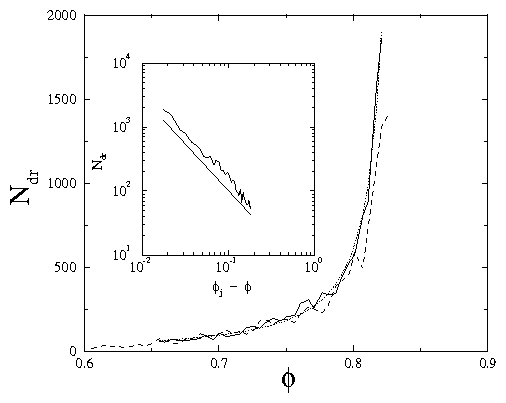
(b) The critical force Fc required to depin the disks vs ϕ/ϕj,
where ϕj is the jamming density in the absence of pinning sites,
for Np/Nj= 0.00138 (blue crosses), 0.00692 (green plus signs),
0.0346 (red triangles), and 0.09267 (black triangles).
(c) Fc vs ϕ/ϕj for
Np/Nj=0.828 (black circles), 0.415 (red squares), and 0.277
(green diamonds).
Figure adapted from ref. 72.
Fig. 6:
Jamming in a system of bidisperse disks driven through an obstacle array.
(a) Jamming diagram for Np/Nj vs ϕ.
Np is the number of obstacles and Nj is the number of disks in an
obstacle-free system at the jamming density.
ϕ is the disk density.
The system is defined to be jammed when the disks do not
continuously move under an arbitrarily small
applied drift force.
Jammed states exist above and to the right of the black line, and unjammed
states are found below the black line.
The red squares indicate the value of ϕ above which the particles
flow as a solid. Near point J, the jamming density decreases linearly with
increasing Np/Nj, while for ϕ < 0.8, the line separating the
jammed and unjammed states is much flatter.
(b) The critical force Fc required to depin the disks vs ϕ/ϕj,
where ϕj is the jamming density in the absence of pinning sites,
for Np/Nj= 0.00138 (blue crosses), 0.00692 (green plus signs),
0.0346 (red triangles), and 0.09267 (black triangles).
(c) Fc vs ϕ/ϕj for
Np/Nj=0.828 (black circles), 0.415 (red squares), and 0.277
(green diamonds).
Figure adapted from ref. 72.
|