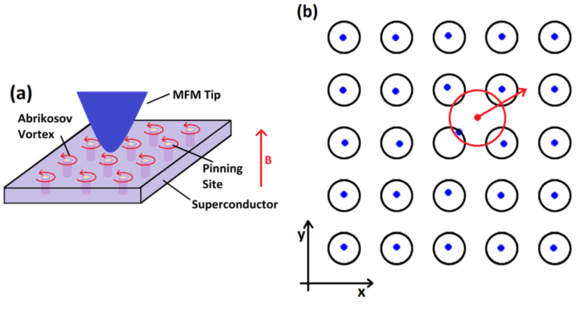
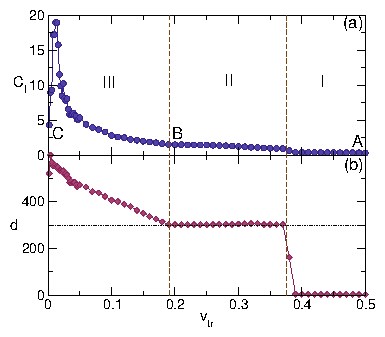
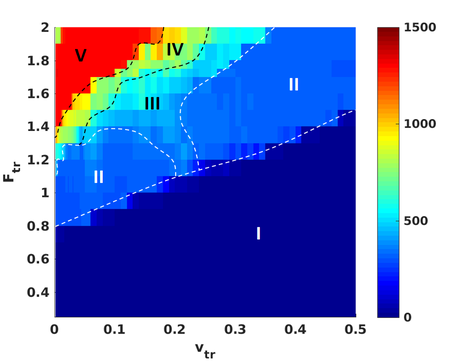
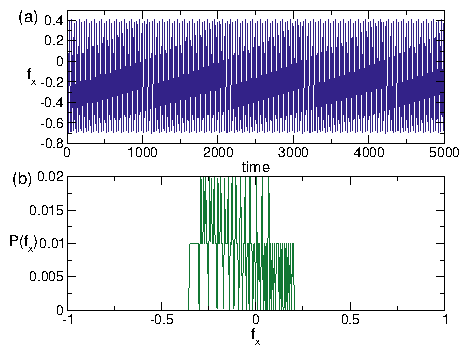
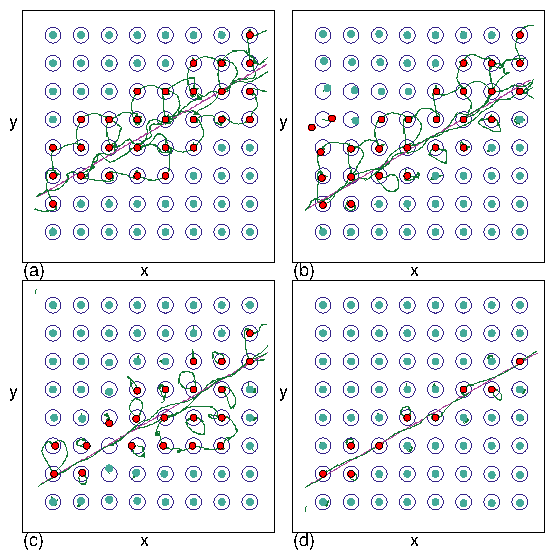
 Figure 5:
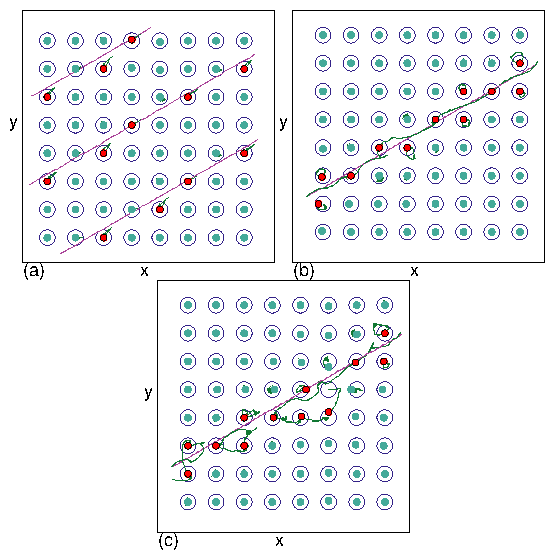
Vortex positions (filled circles), pinning site locations (open circles), tip trajectory
(magenta line), and vortex trajectories (green lines)
in an 8λ×8λ portion of the
Ftr=1.8 system in Fig. 4(c,d).
Red filled circles indicate vortices that were displaced a distance of at least
a pin radius due to the motion of the trap.
(a) At vtr = 0.02 in phase V,
the trap always contains two vortices and correlated ringlike
exchanges of vortices occur in the surrounding regions.
As the trap moves, the two trapped vortices dislodge three pinned vortices, and
one of these vortices jumps into the empty pinning site immediately
behind the moving trap.
(b) At vtr = 0.12 in phase IV, the trap alternates between capturing one and two vortices.
(c) Disordered flow in phase III at vtr=0.25, with
a much weaker perturbation of the surrounding pinned vortices.
(d) At vtr = 0.5 in phase II, a vortex only travels a short distance with the trap
before exchanging with a pinned vortex.
Figure 5:
Vortex positions (filled circles), pinning site locations (open circles), tip trajectory
(magenta line), and vortex trajectories (green lines)
in an 8λ×8λ portion of the
Ftr=1.8 system in Fig. 4(c,d).
Red filled circles indicate vortices that were displaced a distance of at least
a pin radius due to the motion of the trap.
(a) At vtr = 0.02 in phase V,
the trap always contains two vortices and correlated ringlike
exchanges of vortices occur in the surrounding regions.
As the trap moves, the two trapped vortices dislodge three pinned vortices, and
one of these vortices jumps into the empty pinning site immediately
behind the moving trap.
(b) At vtr = 0.12 in phase IV, the trap alternates between capturing one and two vortices.
(c) Disordered flow in phase III at vtr=0.25, with
a much weaker perturbation of the surrounding pinned vortices.
(d) At vtr = 0.5 in phase II, a vortex only travels a short distance with the trap
before exchanging with a pinned vortex.
|