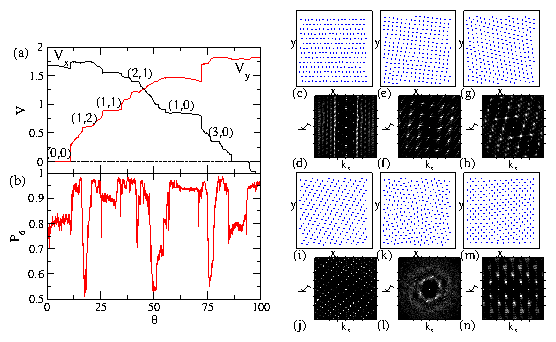
 Figure 1:
(a)
V
vs
θ for vortices moving on a triangular
pinning array
with Fp=1.85 at B/Bϕ=1.5.
Dark line: Vx; light line: Vy. Locking steps
occur at θ = tan−1(√3m/(2n +1)), where m,n are integers.
The locking steps (m,n) at
(0,0), (1,2), (1,1), (2,1), (1,0), and (3,0) are highlighted.
There is also
a locking step at θ = 90°.
(b) The corresponding fraction of sixfold coordinated particles
P6 vs θ.
Changes in P6 are correlated with the velocity locking steps in (a).
(c,e,g,i,k,m) The vortex positions and
(d,f,h,j,l,n) corresponding S(k).
(c,d) The smectic structure along the (0,0) step.
(e,f) Square lattice formation on the (1,2) step.
(g,h) Partial triangular ordering in a non-step region at θ = 36°.
(i,j) The smectic structure on the (1,0) step.
(k,l) An anisotropic liquid at the transition out of the (1,0) step.
(m,n) A distorted square lattice at the locking regime for
θ = 90°
Figure 1:
(a)
V
vs
θ for vortices moving on a triangular
pinning array
with Fp=1.85 at B/Bϕ=1.5.
Dark line: Vx; light line: Vy. Locking steps
occur at θ = tan−1(√3m/(2n +1)), where m,n are integers.
The locking steps (m,n) at
(0,0), (1,2), (1,1), (2,1), (1,0), and (3,0) are highlighted.
There is also
a locking step at θ = 90°.
(b) The corresponding fraction of sixfold coordinated particles
P6 vs θ.
Changes in P6 are correlated with the velocity locking steps in (a).
(c,e,g,i,k,m) The vortex positions and
(d,f,h,j,l,n) corresponding S(k).
(c,d) The smectic structure along the (0,0) step.
(e,f) Square lattice formation on the (1,2) step.
(g,h) Partial triangular ordering in a non-step region at θ = 36°.
(i,j) The smectic structure on the (1,0) step.
(k,l) An anisotropic liquid at the transition out of the (1,0) step.
(m,n) A distorted square lattice at the locking regime for
θ = 90°
|
