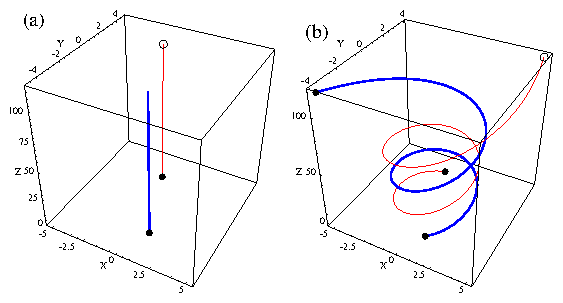
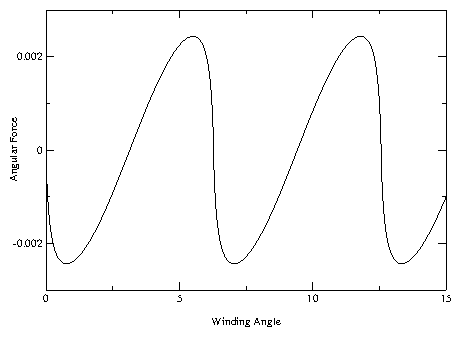
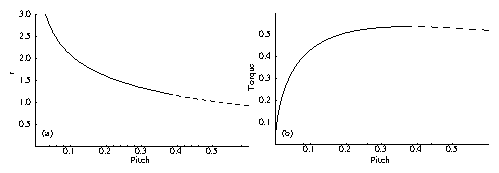
 Figure 2: (a)
r (half the spacing between vortices)
in units of λ and (b) torque on the top end of each
vortex
in units of λ√{~ϵ1ϵ0}
as a function of pitch
∂z θ,
in units of √{ϵ0/~ϵ1}/λ.
The dashed line denotes an unstable vortex configuration
above a pitch of approximately 0.378,
corresponding to a minimum
r ≈ 1.19λ.
Figure 2: (a)
r (half the spacing between vortices)
in units of λ and (b) torque on the top end of each
vortex
in units of λ√{~ϵ1ϵ0}
as a function of pitch
∂z θ,
in units of √{ϵ0/~ϵ1}/λ.
The dashed line denotes an unstable vortex configuration
above a pitch of approximately 0.378,
corresponding to a minimum
r ≈ 1.19λ.
|