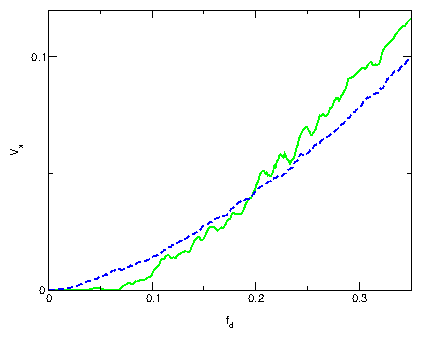
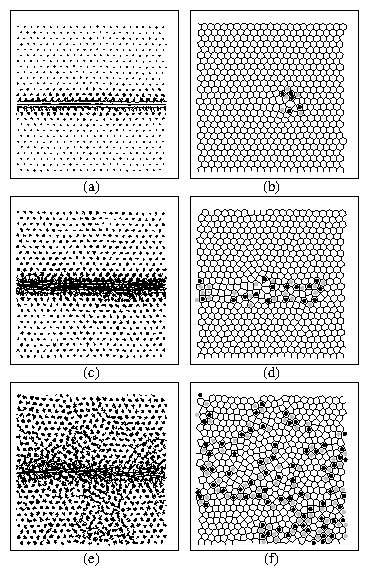
 Figure 1:
(a,c,e): Colloid configurations (black dots)
and trajectory lines at different
temperatures for a driven particle with charge qd/q = 3.
(b,d,f): Corresponding Voronoi construction
colored according
to the number of neighbors: five (black), six (white), and seven (gray).
(a,b) T/Tm = 0.1; (c,d)
T/Tm = 0.57; (e,f) T/Tm = 1.07.
Figure 1:
(a,c,e): Colloid configurations (black dots)
and trajectory lines at different
temperatures for a driven particle with charge qd/q = 3.
(b,d,f): Corresponding Voronoi construction
colored according
to the number of neighbors: five (black), six (white), and seven (gray).
(a,b) T/Tm = 0.1; (c,d)
T/Tm = 0.57; (e,f) T/Tm = 1.07.
|