Nature Communications 9, 4146 (2018)
Ice Rule Fragility via Topological Charge Transfer in Artificial Colloidal Ice
András Libál1,2, Dong Yun Lee3, Antonio Ortiz-Ambriz3, Charles Reichhardt1, Cynthia J. O. Reichhardt1, Pietro Tierno3,4,5 and Cristiano Nisoli1,6
1Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA.
2Mathematics and Computer Science Department, Babes-Bolyai University, Cluj 400084, Romania.
3Departament de Fisica de la Materia Condensada, Universitat de Barcelona, Barcelona 08028, Espana.
4Universitat de Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, Barcelona 08028, Spain.
5Institut de Nanociencia i Nanotecnologia, Universitat de Barcelona, Barcelona 08028, Spain.
6Institute for Materials Science, Los Alamos National Laboratory, Los Alamos, NM 87545, USA.
Artificial particle ices
are model systems of constrained, interacting particles. They have been introduced theoretically to study
ice-manifolds emergent from frustration,
along with
domain wall and grain boundary dynamics, doping, pinning-depinning,
controlled transport of topological defects,
avalanches, and memory
effects.
Recently
such particle-based ices have been experimentally realized
with vortices in nano-patterned superconductors
or gravitationally trapped colloids.
Here we demonstrate that,
although these ices are
generally considered
equivalent
to
magnetic spin ices, they can access
a novel spectrum of
phenomenologies
that
are inaccessible to the latter.
With experiments, theory and simulations we demonstrate
that in
mixed coordination geometries,
entropy-driven negative monopoles spontaneously appear
at a density determined by the vertex-mixture ratio.
Unlike its spin-based analogue, the colloidal system displays a "fragile ice"
manifold, where local energetics oppose the ice rule, which is instead
enforced through conservation of the global
topological charge.
The fragile colloidal ice,
stabilized by topology,
can be spontaneously broken by
topological charge transfer.
Results
The system
Experimental and numerical results
Entropic nature of ice rule fragility
Discussion
Methods
Experimental system
Soft lithographic structures
Numerical simulation
Computation of theoretical curves
References
The ice rule [1] has a long, fascinating history
that has influenced numerous disciplines including thermodynamics, physical chemistry, statistical mechanics, magnetism, materials science, and soft matter. In the 1930s Giaque and Ashley [2,3] found that the specific entropy of water at very low temperature was not zero, despite the ordered, solid structure of ice. In water ice the oxygen atoms reside at the center of tetrahedra, sharing four hydrogen atoms with four nearest neighboring oxygen atoms. Two hydrogen atoms are covalently bound to each oxygen, and two form hydrogen bonds with neighboring oxygen atoms. In the so-called ice rule introduced by Bernal and Fowler [1], this situation is described as having two hydrogen atoms pointing "in", and two pointing "out" of the tetrahedron. As Linus Pauling explained [4], the freedom in choosing such an arrangement on a large lattice leads to a degeneracy that grows exponentially with the number of tetrahedra, generating the residual entropy.
This idea proved to be not limited to water. The ice rule was recognized to occur in exotic magnets, namely the rare earth titanates such as Ho2Ti2O7 and Dy2Ti2O7 [5,6]. These pyrochlore systems were called "spin ices" because the cations Ho3+ and Dy3+ carry a large magnetic moment directed along the lattice bonds which can be associated to a classical, binary Ising spin. At low temperature, frustration ensures that two spins point in and two out of each vertex, reproducing the ice rule and preventing the spontaneous magnetization of the material.
The ice rule was eventually exploited to design new artificial frustrated systems based on magnetic nano-islands, confined colloidal particles, or vortices in superconductors [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] that generalize spin ices and are broadly called artificial spin ices. There, exotic states of matter and emergent dynamics often not found in natural systems can be deliberately designed and externally controlled in
artificial nano- and
micro-scale materials.
In such systems frustration produces
complex disordered manifolds where fascinating effects, such as
dimensionality reduction [27],
emergent descriptions [28,29,30],
topological constraints [31],
and complex dynamics of magnetic (or more generally topological) charges [17,32,33]
can be tailored, nano- or micro-engineered, and characterized at the level of the constitutive degrees of freedom, often providing
remarkable vistas of statistical mechanics in action [34,35,36].
Such generality is not surprising since the ice-rule is a powerful topological prescription for conceptualizing the effects of frustration in a broad class of physical systems.
To understand the topological nature of the ice rule in the broadest generality, consider a general lattice, even a graph, or network [37] with nodes of various coordination number z. Assign binary variables on the edges of the graph, in the form of spins directed along the edges and impinging in the nodes. Then we can define a "topological charge" q for each vertex as the difference in the number of spins n pointing toward the vertex and the number of spins z−n pointing away from it, or q=2n−z. In magnetic spin ices q is proportional to the magnetic charge of the vertex [38,39] leading to a rich phenomenology for magnetic charge currents [40], charge ordering [41,42], charge screening [28,32] or dynamical arrest [43].
In this language, the ice rule corresponds to the minimization of the absolute value of the topological charge |q|. The charge is called "topological" insofar as it depends upon the connectivity of the system, and its definition does not change for continuous deformations of the lattice. It is therefore a topological invariant for the vertex configuration (though it does not completely define the spin configuration [44,30,33]). On vertices of even coordination the minimization of |q| on each vertex implies that q=0, and when z=4 we recover the original 2-in/2-out ice rule of water ice. On vertices of coordination z=3, the minimum occurs for q=±1, corresponding to 2-in/1-out or 1-in/2-out.
In the magnetic spin ice-like systems mentioned above, the low energy ensembles all obey the ice rule, which has proven to be extremely robust. The ice rule survives all sorts of weak or strong alterations, including decimation [29],
mixed coordination [28,27],
and the introduction of dislocations [31]; indeed
it was found that even isolated clusters of magnetic vertices
obey the ice rule at low energy [45].
Here we add a new chapter to the already rich history of the ice rule by introducing a system where the ice rule becomes "fragile", meaning that it can be easily destabilized by topology. Through a combination of theory, simulations, and experiments,
we
demonstrate that the colloidal ice
falls in a new class of geometrically frustrated ices,
or "fragile ices." There, the ice rule is spontaneously broken
in lattices of mixed coordination, leading
to a rich and unique set of
phenomena, including topological charge transfer and charge screening,
that are completely absent in nanoscale magnetic ices or indeed in most ice systems known to us.
It is important to understand that we are describing fragility, not a breakdown. As we will see, most of the system still obeys the ice rule, and only specific charges, in the form of negative monopoles, appear. Crucially, these monopoles are not excitations, but instead belong to the low energy state, and their density can be controlled.
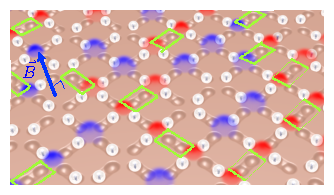 Figure 1: Schematic of the system.
The experimental system consists of paramagnetic colloids placed via optical tweezers in lithographic double wells
arranged along the edges of a square lattice. Each colloid is gravitationally trapped in one microgroove, and it can sit in one of the two wells. A perpendicular field →B magnetizes the colloids, thus introducing a repulsive dipolar interaction. The edges of the square lattice can be decimated by simply removing the colloids from the corresponding microgrooves (dashed green rectangles). Red and blue glows denote positive and negative topological charges, respectively.
Figure 1: Schematic of the system.
The experimental system consists of paramagnetic colloids placed via optical tweezers in lithographic double wells
arranged along the edges of a square lattice. Each colloid is gravitationally trapped in one microgroove, and it can sit in one of the two wells. A perpendicular field →B magnetizes the colloids, thus introducing a repulsive dipolar interaction. The edges of the square lattice can be decimated by simply removing the colloids from the corresponding microgrooves (dashed green rectangles). Red and blue glows denote positive and negative topological charges, respectively.
|
Results
The system.
The content of this article can be summarized by referring to its figures. In Figs. 1 and 2 we illustrate the system: repulsive colloids are gravitationally trapped in microgrooves with two preferential positions at the extremes, making each groove equivalent to a binary Ising spin. The grooves are arranged along the edges of a square lattice, the colloids repel each other, and the system obeys the ice rule (Figure 3a), as already found in Refs. [11,12,13,23]. When we decimate our system by removing colloids (Figure 2), we obtain a lattice of mixed z=3,4 coordination. There, we observe, the ice-rule is spontaneously yet selectively violated as negative q=−2 charges form on the z=4 vertices (Figures 3 and 4). The z=3 vertices still all obey the ice rule; however, the relative ratio of q=1 q=−1 charges changes in order to compensate the negative charge of the z=4 vertices (Fig. 5), since the total topological charge of a system of "dipoles" must remain zero. This global fragility of the ice rule introduces further local phenomenology, as charges also rearrange locally to screen the q=−2 monopoles appearing on z=4 vertices (Figure 5).
This happens because, as previously noted by one of us [46,47], the
ice rule in magnetic spin ice systems
is enforced locally by the vertex energetics, but globally
in colloidal spin ices, by
the conservation of topological charge.
In fact, in colloidal systems the ice rule is
actually opposed by the local vertex energy, as we explain below.
Since magnetic ices are locally at an energy minimum, they are
structurally "robust" ices. In contrast,
the colloidal ice has a collective low-energy manifold
that is composed of an energetic compromise between locally excited vertices and
is thus a "fragile" ice.
Since the resulting energetically unstable arrangement is stabilized by topology, it can also be easily and deliberately
destabilized through topology to create new
emergent states.
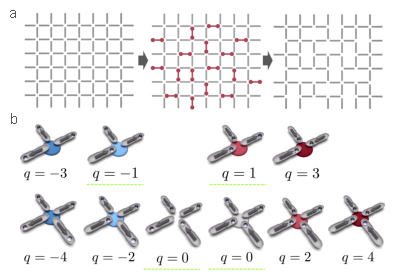 Figure 2: Schematics of the decimation.
a) A decimation of the square lattice that creates only z=3 and z=4 vertices, but no z=2 vertices, is equivalent to a partial dimer covering (red dumbbells) of the edges. b) Colloid configurations for vertices of coordination z=4,3, in order of increasing topological charge and thus energy. The ice rule vertices have minimal absolute charge, which is q=±1 for z=3 vertices and q=0 for z=4 vertices (dashed green underline), and yet, unlike in magnetic spin ice, their energy is not the lowest. Red (blue) disks denote positive (negative) charges. A gray disk on a z=4 vertex indicates a zero charge excitation corresponding to a biased ice rule vertex. The vertex without a disk represents the "ground state" of the square ice. Arrows aligned
along the groove and pointing toward the colloids represent the analogy with a spin ice system.
Figure 2: Schematics of the decimation.
a) A decimation of the square lattice that creates only z=3 and z=4 vertices, but no z=2 vertices, is equivalent to a partial dimer covering (red dumbbells) of the edges. b) Colloid configurations for vertices of coordination z=4,3, in order of increasing topological charge and thus energy. The ice rule vertices have minimal absolute charge, which is q=±1 for z=3 vertices and q=0 for z=4 vertices (dashed green underline), and yet, unlike in magnetic spin ice, their energy is not the lowest. Red (blue) disks denote positive (negative) charges. A gray disk on a z=4 vertex indicates a zero charge excitation corresponding to a biased ice rule vertex. The vertex without a disk represents the "ground state" of the square ice. Arrows aligned
along the groove and pointing toward the colloids represent the analogy with a spin ice system.
|
The system under study is shown schematically in Figure 1. We start from an array of bistable traps arranged along the edges of a square lattice. Each trap contains a colloid, gravitationally confined, that can preferentially occupy the two ends of the traps. The colloids are paramagnetic and can be magnetized by a field perpendicular to the plane of the array, introducing repulsive, isotropic, colloid-colloid repulsion. This system is known to obey the ice rule [11,23,24].
We then consider a "decimation" of such an array, in which we remove certain traps (or, equivalently, certain colloids from the traps) in a random fashion, in order to create a lattice of mixed coordination z=3,4.
The result is a decimated square array of traps as shown in Figure 2(a).
Without any decimation protocol, the simple elimination of traps at random from the structure would create vertices of coordination z=3, z=2, and z=1. To reduce complexity, however, we prefer to generate only z=3 vertices through decimation (although our considerations also apply to other cases where z=2 and z=1 vertices are present [46,47]). We achieve our decimation using a partial, random dimer covering of the edges (Figure 2(a)),
where randomly
chosen edges are covered by dimers in such a way that each vertex is covered by at most one dimer. We then remove an edge between two "dimerized" vertices of coordination z=4, in order to obtain only vertices of coordination z=3.
We introduce some nomenclature that will prove to be useful later. Considering the thermodynamical limit of the system, and neglecting boundary effects, we call Nt the number of traps in the original square lattice, which form a total of Nv=Nt/2 vertices of coordination z = 4 (Figure 2(a)). We decimate the lattice by removing Nd traps, in accordance with the dimer model protocol. Each time a trap is removed, two z−4 vertices change into two z=3 vertices.
We call Nz3 and Nz4 the resulting number of vertices of coordination z=3 and 4, respectively. The decimation density is defined as ξ = Nd/Nt,
while η = Nz3/Nz4 is the ratio between the two
vertex types.
Our dimer-cover based decimation strategy thus gives Nz4=Nv−2Nd, Nz3=2Nd, and therefore
η = 4 ξ/(1−4 ξ).
The maximum possible decimation corresponds to a complete random dimer
covering realized when all the vertices are covered by one and only one dimer. Then the number of dimers is half of the number of vertices and therefore a quarter of the number of traps. Thus the maximum decimation corresponds to a removal of 25% of the traps, or ξ = 1/4. Note that η→+∞ when ξ→1/4−,
since Nz4=0 at this maximal decimation: all vertices have coordination z=3.
 Figure 3: Experimental results. (a) An experimental image of the undecimated system shows the expected antiferromagnetic ordered configuration. The blue arrows denote spins associated with the double wells occupied by the colloids. (b-e) Experimental images of the colloidal system at increasing decimation corresponding to (b) η = Nz3/Nz4=0.19 , ξ = Nd/Nv=0.04, (c) η = 1.3158, ξ = 0.142, (d) η = 2.3846, ξ = 0.176 and (e) η = 5.2857, ξ = 0.21. Dashed green rectangles denote decimated traps corresponding to z=3 vertices. Negative charges of q=−2 monopoles (blue glows) form on z=4 vertices as a consequence of decimation, in violation of the ice rule. Meanwhile z=3 vertices still obey the ice rule, but develop an overabundance of q=−1 charges to adsorb the negative charge of the z=4 vertices. This phenomenon increases as decimation increases. Scale bars (yellow) are 20μm. See the Supporting Information (SI) for corresponding movie clips.
Figure 3: Experimental results. (a) An experimental image of the undecimated system shows the expected antiferromagnetic ordered configuration. The blue arrows denote spins associated with the double wells occupied by the colloids. (b-e) Experimental images of the colloidal system at increasing decimation corresponding to (b) η = Nz3/Nz4=0.19 , ξ = Nd/Nv=0.04, (c) η = 1.3158, ξ = 0.142, (d) η = 2.3846, ξ = 0.176 and (e) η = 5.2857, ξ = 0.21. Dashed green rectangles denote decimated traps corresponding to z=3 vertices. Negative charges of q=−2 monopoles (blue glows) form on z=4 vertices as a consequence of decimation, in violation of the ice rule. Meanwhile z=3 vertices still obey the ice rule, but develop an overabundance of q=−1 charges to adsorb the negative charge of the z=4 vertices. This phenomenon increases as decimation increases. Scale bars (yellow) are 20μm. See the Supporting Information (SI) for corresponding movie clips.
|
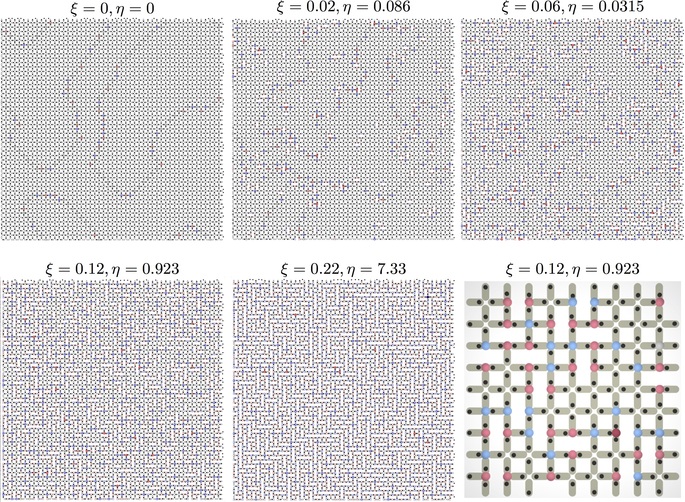 Figure 4: Numerical results. Snapshots of numerical simulations for increasing decimation with color coding as in Figure 2(b) indicating vertex charges. At zero decimation (η = 0)
large regions of the expected antiferromagnetic order separated by domain walls are visible. At low decimation of 2%−6% (η = 0.086, η = 0.315), almost all
of the z=3 vertices are positively charged, while negative charges (q=−2) that appear on the z=4 vertices can pin
the domain walls, causing the ordered domains to shrink. At a decimation of 12%, there is already no discernible order, while at high
decimation, about half of the z=4 vertices violate the ice rule and host positive charges,
which destroy the remaining ordering. In the zoomed portion of the ξ = 12% and η = 0.923 sample, the colloidal positions are visible and show details of violation of the ice rule at z=4 vertices
by negative, q=−2 monopoles only, but little or no ice rule violation at z=3
vertices. See SI for corresponding movie clips.
Figure 4: Numerical results. Snapshots of numerical simulations for increasing decimation with color coding as in Figure 2(b) indicating vertex charges. At zero decimation (η = 0)
large regions of the expected antiferromagnetic order separated by domain walls are visible. At low decimation of 2%−6% (η = 0.086, η = 0.315), almost all
of the z=3 vertices are positively charged, while negative charges (q=−2) that appear on the z=4 vertices can pin
the domain walls, causing the ordered domains to shrink. At a decimation of 12%, there is already no discernible order, while at high
decimation, about half of the z=4 vertices violate the ice rule and host positive charges,
which destroy the remaining ordering. In the zoomed portion of the ξ = 12% and η = 0.923 sample, the colloidal positions are visible and show details of violation of the ice rule at z=4 vertices
by negative, q=−2 monopoles only, but little or no ice rule violation at z=3
vertices. See SI for corresponding movie clips.
|
Figure 2(b) shows the energetics of the resulting vertices of coordination z=3 and z=4 arranged in order of increasing energy, which also corresponds to increasing topological charge. Note that in computing the vertex energy we adopt a nearest neighbor approximation and consider only the interaction of the particles close to the vertex. Vertices of coordination z=4 can have even charges q=−4,−2,0,2,4, whereas vertices of coordination z=3 can have odd charges q=−3,−1,1,3. We label the vertices by their topological charge, and call Nz4,q and Nz3,q the number of vertices of charge q and coordination z=4,3,
respectively. We define the
relative vertex frequencies as
nz4,q=Nz4,q/Nz4 and
nz3,q=Nz3,q/Nz3.
We have performed experiments on mixed-coordination lattices at various levels of decimation. We corroborate our experimental results using overdamped Langevin dynamics on larger samples. For both experiments and simulations, at each level of decimation the results are obtained by averaging over ten different, randomly generated lattices obtained via the random dimer algorithm described above.
Experimental and numerical results
The experimental system is based on a monolayer
of paramagnetic colloids confined above
a square lattice of lithographic, microscopic double-wells (Figure 1).
Each gravitational trap permanently confines a colloid,
and contains a small central hill that the colloid
can cross under the influence of colloid-colloid interactions (see Methods).
We apply
an external magnetic field \bmB perpendicular to the plane
to induce
a tunable, perpendicular
dipole moment \bmm ∝ \bmB in each colloid. The
resulting interaction
between two colloids a distance r apart
is repulsive, isotropic, and given by
Ud ∼ m2/r3.
We use optical tweezers to load one
colloid
into each double-well, or to eliminate
colloids from the traps during lattice decimation.
Using video microscopy and particle tracking,
we extract real-time dynamics and visualize
the collective low-energy configurations. As the field \bmB increases, so does the mutual repulsion, and the colloids, originally disposed randomly, rearrange to a collective low-energy configuration [23,24].
Our experimental system extends over a square lattice composed by 11 ×8 vertices corresponding to a total of Nt = 195 traps in the undecimated case. We note that the size of the experiments is limited by two factors: the trapping objective constrains the field of view, and the time required to populate the system must be small enough to keep the suspension electrostatically stable.
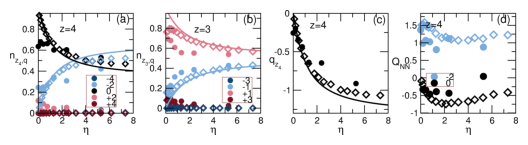 Figure 5: Statistics of experimental results (bullets) and
numerical results (diamonds) compared to theoretical predictions (solid lines).
(a) Vertex statistics nz4,q at equilibrium
vs η = Nz3/Nz4 for z=4 vertices grouped by topological charge q.
Dark blue: q=−4; light blue: q=−2; black: q=0; pink: q=+2;
red: q=+4.
All the non-ice-rule vertices are suppressed except q=−2
monopoles, which increase with η
as the availability of z=3 vertices for charge transfer increases.
(b) Vertex statistics nz3,q vs η for z=3 vertices.
Dark blue: q=−3; light blue: q=−1; pink: q=+1; red: q=+3.
Only ice rule vertices are present (q=±1),
but there is an excess density of positive q=+1 charges
in order to screen the charge transfer from the z=4 sector.
As η→ ∞, the z=4 sector disappears and
thus nz3,q=1 and nz3,q=−1 tend to the same value of
nz3,q=1=nz3,q=−1=1/2,
as also found in kagome ice [44].
(c) Net density of charge qz4
forming on z=4 vertices vs η as a measure of ice rule violation.
(d) Charge screening QNN of q=−2 monopoles (blue)
and "screening" of q=0 ice rule vertices (black) on z=4 vertices
vs η.
At large decimation we find sparse z=4 vertices embedded in
a background of z=3 vertices.
The z=3 vertices
have an average charge of 〈Q3 〉 = +0.15,
but the charge is much larger (〈Q3 〉 = +1.25)
in the nearest neighborhood of q=−2 monopoles.
This indicates that the disordered sea of z=3
charges screens the monopoles.
Figure 5: Statistics of experimental results (bullets) and
numerical results (diamonds) compared to theoretical predictions (solid lines).
(a) Vertex statistics nz4,q at equilibrium
vs η = Nz3/Nz4 for z=4 vertices grouped by topological charge q.
Dark blue: q=−4; light blue: q=−2; black: q=0; pink: q=+2;
red: q=+4.
All the non-ice-rule vertices are suppressed except q=−2
monopoles, which increase with η
as the availability of z=3 vertices for charge transfer increases.
(b) Vertex statistics nz3,q vs η for z=3 vertices.
Dark blue: q=−3; light blue: q=−1; pink: q=+1; red: q=+3.
Only ice rule vertices are present (q=±1),
but there is an excess density of positive q=+1 charges
in order to screen the charge transfer from the z=4 sector.
As η→ ∞, the z=4 sector disappears and
thus nz3,q=1 and nz3,q=−1 tend to the same value of
nz3,q=1=nz3,q=−1=1/2,
as also found in kagome ice [44].
(c) Net density of charge qz4
forming on z=4 vertices vs η as a measure of ice rule violation.
(d) Charge screening QNN of q=−2 monopoles (blue)
and "screening" of q=0 ice rule vertices (black) on z=4 vertices
vs η.
At large decimation we find sparse z=4 vertices embedded in
a background of z=3 vertices.
The z=3 vertices
have an average charge of 〈Q3 〉 = +0.15,
but the charge is much larger (〈Q3 〉 = +1.25)
in the nearest neighborhood of q=−2 monopoles.
This indicates that the disordered sea of z=3
charges screens the monopoles.
|
In Figure 3 we show snapshots of experimental results for
different decimations. At zero decimation, the system obeys the ice rule, as shown in Figure 3(a). At nonzero decimation, the ice rule is broken
in the z=4 sublattice, but very specifically: only q=−2 charges appear spontaneously, while all other vertex type follow the ice rule.
At the same time, the ice rule is still obeyed on the z=3 sublattice, where only charges q=±1 are present.
We corroborate these experimental findings with numerical simulations on larger samples (2500 vertices with periodic boundary conditions) than those used in experiments (which contained only 88 vertices). We employ over-damped, Brownian dynamics precisely parametrized to mimic the experimental setting (see Methods and ref [17,48]).
In Fig. 4 we show snapshots of the results of simulations at different decimation levels. Exactly as in the experiment, the simulations confirm that breakdown of the ice rule occurs on z=4 vertices only. Furthermore, on a larger scale we find that the disordered charge transfer between z=4 and z=3 vertices implies the breakdown of the well known antiferromagnetic order [11,8] of the square ice manifold. This structural transition to disorder has been recently
proved theoretically [47], but here we experimentally observe it at a decimation of approximately 12% of the traps, about halfway to the maximal decimation of 25%.
In Fig. 5 we provide a quantitative analysis of the numerical and experimental results along with our theoretical predictions, which are described later. In Fig. 5(a, b) we plot the relative frequencies nz4,q and nz3,q of vertices grouped by topological charge versus η = Nz3/Nz4, the ratio between the two
vertex coordinations. Figure 5(a) shows more precisely
that in the z=4 sector vertices obey the ice rule, with the only violations arising from negative topological monopoles of charge q=-2. These negative charges appear spontaneously and
increase in relative number as the amount of decimation increases, which increases the strength of the violation of the ice rule on vertices of coordination z=4. A measure of ice rule violation, the total density of negative charge qz4=∑q nz4,q q
appearing on the z=4 vertices, is plotted in Fig. 5(c) as a function of the lattice decimation.
Remarkably we find that
the z=3 vertices (Fig. 5(b)) always obey the ice rule,
as was theoretically proposed in [46,47]. Indeed, only charge q=±1 vertices are present for all but the very lowest decimations, with small deviations at η < 1 (see later).
Figure 5(b) also shows that q=1 vertices always exceed q=−1 vertices in number and thus the z=3 vertices have an overall positive charge.
They can therefore adsorb the extra
negative charge introduced by the
z=4 vertices without
leaving the ice-manifold simply by shifting their
relative ratio in favor of vertices of charge q=1. Moreover, Figure 5(b) indicates that as η = Nz3/Nz4 tends to infinity (which means that the density of z=4 vertices tends to zero), the fraction of vertices of charge q=1 and q=−1 both tend to the same value of 1/2 as expected in a single coordination, z=3 lattice.
Small deviations from this picture only happen at η < 1. There, z=3 vertices are sparse and surrounded by z=4 vertices. The density of z=3 is too small to adsorb all the available charge coming from the z=4 and therefore the numerical simulations show larger q=+3 charges forming on them. In the experimental data only, we also see very few q=+2 monopoles forming on z=4 vertices at low decimation. This is likely a consequence of lack of complete equilibration at low decimation, where the system is close to order, and of the finite size of the sample, where positive charges can form on the boundaries as explained in the next subsection and in ref. [47]. Indeed, this type of defects was also present in previous work on non-decimated, ordered square lattice systems [23].
Moving away from the global picture, disorder of the ensemble produces fascinating local effects of spontaneous screening of topological charge. In Figure 5(d) we plot QNN, the average charge neighboring a z=4 vertex. We find that negative q=−2 monopoles are surrounded by a positive average charge that largely exceeds the average charge surrounding non-charged z=4 vertices. Thus, as monopoles of charge q=−2 spontaneously appear on z=4 vertices, they are screened by positive charges q=1 on the surrounding vertices of coordination z=3. This suggests that
charge screening is not unique to magnetic charges that interact via
a Coulomb law in magnetic ices [44,33,28,32].
In fact, charge rearrangement and ordering was also recently observed numerically in the disordered ensemble of kagome colloidal ice [48]. There, it was shown, it is a consequence of the 1/r3 long range interaction among colloids, the same present in this work. Charge effects driven by charge-charge interactions were also seen in magnetic ice systems: charge ordering within the ice state of kagome artificial spin ice [42,41], and monopole screening by magnetic charges in Shakti ice [28]. Unlike in Shakti, here charges screen not excitations, but rather monopoles which belong to low energy state. Given the disordered nature of the allocation of these negative monopoles,
These results unambiguously demonstrate the breakdown of the ice rule in particle based ice as suggested in Ref. [46], along with non-trivial rearrangement of the topological charge being transferred.
We reiterate that such a breakdown is not possible
in magnetic spin ice systems, where the ice manifold has been shown to be
completely robust [29,28,27,31,45].
Entropic nature of ice rule fragility
To understand the nature of the ice rule breakdown in colloidal ice, we first need to
understand its origin, as the former differs essentially from the magnetic ices.
In magnetic spin ice
the topological charge minimization that corresponds to the ice rule is enforced by the local energetics,
since the energy of frustrated spins
meeting at a vertex typically scales quadratically with the
vertex charge, or E ∼ q2
(ignoring geometrical effects [38]).
In colloidal ices, however, the energy of s repulsive colloids in a vertex scales
as Es ∼ s(s−1)/2 ∼ qs2/8+qs(z−1)/4 [46],
thus favoring vertices of large, negative charge,
in violation of the ice rule.
Obviously, the total charge must be zero, so it is not possible for
all vertices to be negatively charged. Individual
vertices can only push their charge to the boundaries, and the resulting
charge accumulation
is limited by the size of the edges.
Therefore, the density of topological charge in the bulk
must scale at least as the reciprocal length of the boundaries,
leading to the emergence of the ice rule (zero charge) in the thermodynamic limit. There is thus a collective, non-local reason for the ice rule in colloidal systems, which is quite unlike the local, energy-enforced origin of the ice rule in magnetic systems. Indeed, the latter is observed locally even in small spin ice clusters [45].
The boundary size constraint is lifted in our decimated system,
since the z=4 vertices now have an internal boundary
consisting of z=3 sub-lattices onto which
topological charges can be pushed.
Because the global charge must remain zero,
the two sub-lattices develop opposite nonzero charges.
As a consequence, the ice rule is
very selectively broken in the z=4 sector
by the appearance of negative charges q=−2,
corresponding to 1-in/3-out vertices.
The ice rule still applies to the z=3 vertices, since
the plasma of charges in an odd-coordination spin
ice can absorb and screen charges without breaking the ice rule.
We now make these considerations more quantitative
[46].
For simplicity, we can treat vertices as uncorrelated, but constrain the total charge to be zero. Then the thermodynamic ensemble at equilibrium still follows a Boltzmann distribution but in the effective
vertex energies ~Es=Es−qsϕ, where ϕ is a Lagrange multiplier enforcing the requirement of zero total charge. Thus, for a lattice of coordination z, the choice ϕ = (z−1)/4 returns a spin-ice-like effective energetics,
given by
Es ∼ qs2,
that explains the ice rule of colloidal ice in simple lattices.
When the lattice has multiple coordinations,
however,
there is no single value of ϕ
that can generate
an effective ice-like energetics for vertices of more than one coordination. For z=4,3, charge conservation imposes ϕ = (3−1)/2=1/2 and thus the effective energetics maintains the ice rule on z=3 vertices.
On z=4 vertices, however, it ascribes the same effective energy to the negative (q=−2) monopoles and to the ice rule (q=0) vertices [46]. This explains why those are the only vertices seen in our simulations and experiments.
Another way to understand the same effect was reported recently [47]. It was demonstrated theoretically that a decimated particle-based ice is energetically equivalent to a spin ice stuffed with extra, negative topological charges, placed at the two ends of each decimated trap. For a spin system this implies accumulation of positive charge on decimated vertices (in the current system, z=3 vertices) and, because the total charge of the occupied traps must be zero, the consequent formation of negative monopoles on undecimated vertices (here z=4) vertices.
From these considerations one can quantitatively predict the charge transfer and thus the vertex statistics using a very simple entropic argument. In Methods we show how to obtain a very simple entropy density based on the simplifying assumption of uncorrelated vertices. Such entropy
depends only on the amount of the charge transferred qz4. By maximizing that entropy, we obtain qz4,
which is plotted in Fig. 5(c). Since
the vertex populations are controlled by the charge transfer, we also obtain all the other relevant nonzero quantities.
Our purely entropic predictions in Figure 5,
obtained without any fitting parameters,
agree remarkably well
with the numerical
results of simulations of large lattices with periodic boundary conditions. Small deviations from the theoretical predictions at low decimation come from the simplifying hypothesis of uncorrelated vertices. While such an assumption works well in a disordered ensemble, it is expected to produce deviations from the numerical results at low decimation η < 1 where the system is still largely in an ordered state (see also Figure 4).
We also find very good agreement
with the experimental data. There,
deviations
occur due to the limited size of the system which
inevitably causes some charges to be confined at the boundaries. The agreement confirms the purely entropic nature of the ice rule fragility in this system as explained in the previous subsection.
The
focus of this work is to prove the ice rule fragility in particle-based ices.
We now
describe another interesting effect brought
about by the topological charge entropy which
invites further study: the breakdown of order in the system. Undecimated square ice is antiferromagnetically ordered [11,23]. It has been recently proved theoretically [47] that
under decimation,
square ice crosses through a structural transition to disorder.
At zero temperature, the system is ordered below a critical decimation, and disordered above it. The exact value of
the critical decimation has not been computed exactly (though our current numerical analysis places
it at about 10%, or ξ ∼ 0.1); it corresponds to a percolation threshold in the dimer model on which our decimation protocol is based [47], a subject currently under numerical study by others [49]. The formalism reported above and in [46], relying on uncorrelated charges, applies to disordered manifolds, and therefore does not predict such
a transition.
Clearly in the low-decimation, ordered phase there no topological charge transfer and no ice-rule fragility is predicted. Instead we see in Figure 4 that the breakdown of the ice rule is continuous
as a function of decimation. The reason is that our numerical model is a Brownian dynamics simulation devised to faithfully reproduce the experimental apparatus; like the latter, it does not reach the true ground state but enters a state close to it [17,23]. For instance, the first panel of Figure 4 (zero decimation) shows the presence of ordered domains separated by domain walls. These contain topological charges, though their net charge is zero.
It is easily proven that the negative and positive charges of these
excitations must alternate along such domain walls in
the absence of decimation,
giving no net charge transfer.
At low decimation, as shown in Figure 4, the domain walls pin to the decimated plaquettes,
which preferentially
carry preferably negative charge (a situation analogous to that of doped colloidal ice [19]).
The charge alternation is thus broken on those pinning sites,
generating a net topological charge on the z=4 sector.
This mechanism is better understood by considering how the disorder of the ground state sets in above critical decimation. Following ref. [47], the residual entropy of the ground state and the topological charge transfer
are associated with the appearance of emergent lines composed solely of negative charges, connecting q=−2 monopoles on the z=4 vertices that belong to decimated plaquettes. These lines must thread through nearest neighboring decimated plaquettes, and thus they exist only at decimations large enough
that the decimated plaquettes
percolate. Below that threshold, in the ground state, no such emergent
lines exist,
no topological charge transfer
occurs, and the system remains ordered.
The lines can still appear as small energy excitations, where they must include not only q=−2 monopoles, but also ice rule vertices that do not belong to the ground state (more precisely the fourth vertex from the left in the second line of Figure 2(b),
depicted as a gray disk).
These excited
emergent lines can still thread through decimated plaquettes even when the latter are not percolating. As the decimation is further reduced,
such lines
become simple domain walls,
shown pinned to the decimated plaquettes in Figure 4 at low decimation (ξ = 0.02, 0.06).
Thus we have the following interesting picture: in the
equilibrium ground state
below a critical decimation, the system is ordered and obeys the ice rule, while above
it the system is disordered and the ice-rule is violated [47]. In slightly excited states
at low decimation, the system forms ordered domains separated by lines pinned to the decimated plaquettes. As
the decimation increases, these domains shrink, until at the percolation threshold for the decimated plaquettes, no order is discernible. This mechanism is apparent in the panels of Figure 4 and consistent with
previous
observations in doped colloidal ice [19]. While the domains of the system are strongly correlated
at low decimation,
the domain walls are not, explaining why our uncorrelated-charge treatment above can capture the numerical data even at low correlation, and
testifying to the solidity of the use of topological charges as degrees of freedom for
describing this phenomenon. Indeed it was suggested [47] that
dynamical arrests of the topological charges, though not necessarily of the colloids,
could occur. The associated weak ergodicity breaking might thus make it impractical to observe the predicted structural transition in real systems, an issue that invites further theoretical and experimental investigation.
Discussion
We have added a new chapter to the long history of the ice rule by demonstrating the fragile nature of particle-based ice. Previously the magnetic ice rule had proven remarkably robust to the introduction of all types of structural defects, doping, or dislocations. In contrast, in colloidal ice, the ice manifold
is of a collective, non-local origin
and can be destabilized by topology,
leading to the spontaneous formation
and accumulation of extensive topological charges which can rearrange and screen.
Our work has implications beyond ice rule systems for understanding classical topological phases. For example, the ensemble of ice-rule-obeying configurations, most of which are disordered, is called a Coulomb phase and is an example of a topological phase [50,51,52]. Topological states are increasingly studied in classical settings and in soft matter systems [53,54,55], where they are generally associated with stability produced by topological protection. In this context, our work poses a new set of questions regarding whether such topological protections are robust to dilution or are instead fragile.
Furthermore, from an applied perspective,
the possibility of controlling the dynamics and flow properties
of topological charges via lattice decimation
can inspire the engineering of novel dissipation-free
magnetic storage and logic devices
at the micro and nano-scale.
For example, in domain wall engineering, interfaces of mixed coordination
would be charged and possibly semi-permeable to defects,
while in driven kinetics, entropically spontaneous charges
could be suppressed or enhanced by an ac driving field.
More fundamentally, geometric frustration is a topic of considerable interest, as it
encompasses a large class of physical systems in condensed matter and
beyond, including biological systems. The ice-rule [4,1] has played a fundamental role in frustration, inspiring celebrated theoretical models [56,57] and appearing in an increasing number of physical and non-physical systems [58,37].
Our findings open a path toward
an entirely new phenomenology in geometrically frustrated, ice-rule based systems that is completely absent in traditional spin ices.
Methods
Experimental System
The samples used in this work were
prepared following
a process similar to that described in Refs. [23,24].
In brief (see Figure 6), we use soft lithography
to create two-dimensional square lattices of bistable topographic traps,
each
21 μm in length and
7 μm in width.
The lattice constant is 29 μm.
Each double well has a lateral confinement
of depth ∼ 3 μm and contains a central hill
with average elevation
〈h 〉 = 0.32 ±0.08 μm (see
Figs.1(a,b) in the SI).
Within the trap we deposit paramagnetic colloidal particles
that are 10 μm in size and that have a
magnetic volume susceptibility of χm=0.023 ±0.002.
The particles were diluted in highly deionized water
and
allowed to sediment above the sample
due to density mismatch.
To load one particle per double well, we use optical tweezers made with
a λ = 975 nm, P=330 mW butterfly laser diode focused by an oil immersion Nikon Plan Fluor 100× objective (NA=1.4).
The optical tweezers is mounted in a custom inverted optical microscope
equipped with a white light illumination LED
(MCWHL5 from Thorlabs) and a CCD camera
(Basler A311f).
The external magnetic field is applied
with a custom-made coil oriented perpendicular to
the sample cell and connected to a computer controlled
power amplifier (KEPCO BOP-20 10M).
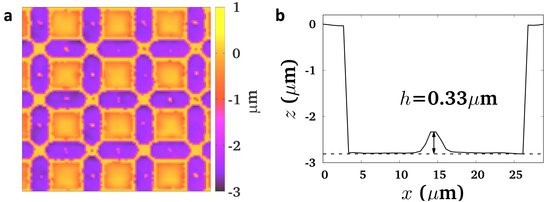 Figure 6: (a) Optical profilometer image of the square lattice
of double wells after the lithographic process.
(b) Profile of one double well characterized by a central hill of elevation h=0.33 μm.
Figure 6: (a) Optical profilometer image of the square lattice
of double wells after the lithographic process.
(b) Profile of one double well characterized by a central hill of elevation h=0.33 μm.
|
Soft lithographic structures
For the
lithographic fabrication procedure,
we write a square lattice of double wells
on a mask made by a 5-inch glass
wafer and covered with a 500 nm layer of Cr.
Direct Write Laser Lithography (DWL 66, Heidelberg Instruments
Mikrotechnik GmbH) was used for this purpose,
based on a 405 nm laser diode
and working at a speed of 5.7 mm2 min−1.
The structures are designed using commercial software (CleWin 4, PhoeniX Software).
Each double well is drawn on the mask as a stadium-shaped transparent region, with a small rectangular opaque spot in the center.
The outer region has a length of 21 μm and a width of 7 μm,
while the spot covers an area of 3 μm ×2 μm.
The Cr mask is then used to etch the microfeatures on a 2.8μm layer of photoresist AZ-1512HS (Microchem, Newton, MA).
The photoresist is deposited on top of a 100μm thick glass coverslip by spin coating (Spinner Ws-650Sz, Laurell) at
500 rpm for 5 seconds and afterwards at 1000 rpm for 30 seconds, both steps with an acceleration of 500 rpm/s.
Different thicknesses of the photoresist could be obtained by varying the rotating speed; however, we find that ∼ 3 μm works well to create
topographical traps capable of capturing the particles within the double wells for most of the applied fields.
After the deposition process, the photoresist is irradiated with UV light passing through the
Cr mask for 6s at a power of 25 mW/cm2 (UV-NIL, SUSS Microtech).
The light passing through the motifs of the mask uncrosslink only the exposed part of the photoresist.
The exposed parts are then eliminated by submerging the
film in a AZ726MF developer solution (Microchem, Newton MA).
At this thickness, the size of the spot is too small for the lithographic process, and results in a small hill with a lower height at the center of the islands.
Numerical simulation
We conduct Brownian dynamics simulations of the decimated
colloidal ice system
comprised of magnetically interacting colloids with a radius of 5.15μm
placed in an array of Nt=50×50×2 = 5000 etched double-well grooves
arranged in a square lattice
with a lattice constant of 29μm giving a total of Nv = 2500
vertices. We use periodic boundary
conditions in both the x and y directions. The double-well trap consists of two halves of a parabolic well joined by an elongated part. The particle in either parabolic half is tethered to the center of the well with spring constant of 1.212 pN/μm. Along the elongated part of the pinning site, this same tethering force confines the particle perpendicularly, while a repulsive force with a spring constant of km = 0.352 pN/μm repels the particle from the middle of the pinning site, reaching a maximum value of Fm=1.758pN in the middle of the pin and vanishing as it reaches the center of either well. These combined substrate forces acting on particle i are written as Fsi.
Magnetization of the particles in the z direction produces a repulsive
particle-particle interaction force Fpp(r)=Ac/r4 with
Ac=3×106χm2 V2 2B2/(2πμ) for particles a distance r apart.
Here χm is the magnetic susceptibility, V is the particle volume,
B is the magnetic field in mT, and all distances are measured in μm.
This gives Fpp=7.231pN for r=20μm at B=50 mT, the maximum field
we consider. The dynamics of colloid i are obtained using the following
discretized overdamped equation of motion:
|
|
1
μ
|
|
∆ri
∆t
|
= |
⎛
√
|
|
kB T N[0,1] + Fppi + Fsi |
| (1) |
where the diffusion constant D=7000 nm2/s,
the mobility μ = 1.729 μm/s/pN
and the simulation time step ∆t = 1ms. The first term on the right is a
thermal force consisting of Langevin kicks of magnitude FT=2.163 pN corresponding
to a temperature of t=20°C (when N[0,1]=1). Here, N[0,1] denotes a random number drawn from a normal (Gaussian) distribution with a mean of 0 and a standard deviation of 1. Each trap is initially filled with a single particle
placed in a randomly chosen well, or left empty in the case of decimation. We increase B linearly
from B = 0 mT to B = 50 mT, consistent with the experimental
range. We average the results
over 10 simulations performed with different random seeds.
Computation of theoretical curves
We
let Nz4,s, Nz3,s
denote the number of vertices containing s colloids and having coordination z=4,3, respectively.
From
this, nz4,s=Nz4,s/Nz4 and nz3,s=Nz3,s/Nz3 are the relative frequencies of vertices with s colloids in each sector. Finally,
we write qz4, qz3
for the total densities of topological charge on the sublattices z=4, z=3, which are given by qz4=∑s=04qs nz4,s, qz3=∑s=03qs nz3,s.
As explained above and demonstrated in Ref. [46], at equilibrium all the z=4 vertices are expected to be either obeying the ice rule-and thus
of
type 2-in (q=0)-or to break the ice rule as lowest charge monopoles-and
thus of
type 1-in (q=-2).
In contrast,
all the z=3 vertices must obey the ice rule, meaning that they are of
type 2-in (q=1) and 1-in (q=−1). The z=3 vertices screen the extra charge by changing the relative admixture of ±1 charges. From the conservation of topological charge, we obtain the constraint
which implies that a complete transfer of topological charge (nz4,1=1, nz4,2=0) is possible in principle when η ≥ 2.
Since configurations corresponding to partial charge transfer are in general entropically favored,
the charge transfer is mostly entropic. Consider a charge transfer between two vertices of different coordination as in Fig 1-Methods. If we ignore the small energy differences between ice-rule vertices, on both vertices the energy depends on the number of colloids in the vertex, and the charge transfer does not change the energy. To demonstrate the entropic nature of the charge transfer, we have shown in the main text that the ensemble can be quantitatively predicted by a purely entropic argument, which we report here.
Consider the entropy
s
=n_z_4,1(n_z_4,1/4)+n_z_4,2(n_z_4,2/2)
|
+ n_z_3,1(n_z_3,1/3)+ n_z_3,2(n_z_3,2/3) ,
where the denominators within the logarithms corresponds to the multiplicity of the respective vertex configurations at the numerators. We can minimize the entropy (3) under the constraints nz4,1+nz4,2=1, nz3,1+nz3,2=1, and Eq. (2). We thus obtain
the density of topological charge per unit of z=4 vertex qz4=−2 nz4,1 as
|
qz4= |
1
2
|
| ⎛
⎝
|
√
|
9 η2+8 η+16
|
−3 η−4 | ⎞
⎠
|
, |
| (3) |
plotted in Figure 4(c) of the main text, and which is
smaller in absolute value
than the maximal charge qtotmax permitted by the geometry,
given by qtotmax=−η if η ≤ 2 and qtotmax=−2 if η ≥ 2. Indeed, Eq. (4) gives qz4→ −4/3 as η→ ∞. Knowledge of charge transfer from Eq. (4) allows us to obtain all other relevant nonzero quantities: qz3=−qz4/η, nz4,1=−qz4/2, nz4,2=1−nz4,1, which are plotted in Figure 4 of the main text.
Data Availability
All relevant data are available from the authors.
Acknowledgements
DYL, AOA and PT acknowledge support from
the ERC Starting grant "DynaMO" (No. 335040).
AOA acknowledges
support from the "Juan de la Cierva" program (FJCI-2015-25787).
P.T. acknowledge support from the Spanish MINECO (FIS2016-78507-C2) and DURSI (2017SGR1061).
The work of CR, CJOR, and CN was carried out under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy at Los Alamos National Laboratory under Contract No. DEAC52-06NA25396. CR and CN wish to thank LDRD at LANL for financial support through grant 20170147ER.
Author contributions
CN originated the idea, provided its theoretical understanding, and supervised the project. AL performed the early
numerical exploration to assess viability of an experiment, followed by full-scale, comprehensive simulations on large
systems, in collaboration with CR and CJOR. AO and DYL performed the experiment with equal contribution, under the
guidance of and in collaboration with PT. All coauthors contributed equally to the analysis of numerical and experimental
outcomes. CN drafted the manuscript with help from CJOR. All coauthors contributed equally to the finalization of the manuscript, figures
and supplementary information.
Additional information
Supplementary Information accompanies this paper at
https://doi.org/10.1038/s41467-018-06631-1.
Competing Interests:
The authors declare no competing interests.
Reprints and permission information is available online at
http://npg.nature.com/reprintsandpermissions/
References
- [1]
-
Bernal, J. & and
Fowler, R.
A theory of water and ionic solution, with particular reference to hydrogen and
hydroxyl ions.
J. Chem. Phys.
1, 515-548 (1933).
- [2]
-
Giauque, W. &
Ashley, M. F.
Molecular rotation in ice at 10 K. Free energy of formation and entropy of water.
Phys. Rev. 43,
81 (1933).
- [3]
-
Giauque, W. &
Stout, J.
The entropy of water and the third law of thermodynamics. The heat capacity of
ice from 15 to 273 K.
J. Am. Chem. Soc.
58, 1144-1150 (1936).
- [4]
-
Pauling, L.
The structure and entropy of ice and of other crystals with some randomness
of atomic arrangement.
J. Am. Chem. Soc.
57, 2680-2684 (1935).
- [5]
-
Harris, M. J.,
Bramwell, S. T.,
McMorrow, D. F.,
Zeiske, T. &
Godfrey, K.
Geometrical frustration in the ferromagnetic pyrochlore Ho2Ti2O7.
Phys. Rev. Lett. 79,
2554 (1997).
- [6]
-
Ramirez, A. P.,
Hayashi, A.,
Cava, R. J.,
Siddharthan, R. &
Shastry, B. S.
Zero-point entropy in 'spin ice.'
Nature
399, 333-335 (1999).
- [7]
-
Brunner, M. &
Bechinger, C.
Phase behavior of colloidal molecular crystals on triangular light lattices.
Phys. Rev. Lett. 88,
248302 (2002).
- [8]
-
Wang, R. F. et al.
Nature
439, 303-306 (2006).
- [9]
-
Nisoli, C.,
Moessner, R. &
Schiffer, P.
Colloquium: Artificial spin ice: designing and imaging magnetic frustration.
Rev. Mod. Phys. 85,
1473 (2013).
- [10]
-
Nisoli, C.,
Kapaklis, V. &
Schiffer, P.
Deliberate exotic magnetism via frustration and topology.
Nat. Phys. 13,
200-203 (2017).
- [11]
-
Libál, A.,
Reichhardt, C. &
Olson Reichhardt, C. J.
Realizing colloidal artificial ice on arrays of optical traps.
Phys. Rev. Lett.
97, 228302
(2006).
- [12]
-
Libál, A.,
Reichhardt, C. J. O. &
Reichhardt, C.
Creating artificial ice states using vortices in nanostructured superconductors.
Phys. Rev. Lett. 102,
237004 (2009).
- [13]
-
Reichhardt, C. J. O.,
Libál, A. &
Reichhardt, C.
Multi-step ordering in kagome and square artificial spin ice.
New J. Phys. 14,
025006 (2012).
- [14]
-
Reichhardt, C. J. O.,
Libál, A. &
Reichhardt, C.
Vortex configurations and dynamics in elliptical pinning sites for high matching fields.
Phys. Rev. B 73,
184519 (2006).
- [15]
-
Libál, A.,
Reichhardt, C. &
Reichhardt, C. J. O.
Hysteresis and return-point memory in colloidal artificial spin ice systems.
Phys. Rev. E
86, 021406
(2012).
- [16]
-
McDermott, D.,
Libál, A.,
Chern, G.-W.,
Reichhardt, C. &
Reichhardt, C. J. O.
Frustration effects and grain boundaries in colloidal particle orderings on optical
substrates.
in Proc. of SPIE
vol. 8810, 881013-1
(2013).
- [17]
-
Libál, A.,
Nisoli, C.,
Reichhardt, C. &
Reichhardt, C. J. O.
Dynamic control of topological defects in artificial colloidal ice.
Sci. Rep.
7, 651 (2017).
- [18]
-
Reichhardt, C. J. O.,
Chern, G.-W.,
Libál, A. &
Reichhardt, C.
Disordered artificial spin ices: avalanches and criticality.
J. Appl. Phys. 117,
172612 (2015).
- [19]
-
Libál, A.,
Reichhardt, C. J. O. &
Reichhardt, C.
Doped colloidal artificial spin ice.
New J. Phys. 17,
103010 (2015).
- [20]
-
Ray, D.
Reichhardt, C. J. O.,
Jankó, B. &
Reichhardt, C.
Strongly enhanced pinning of magnetic vortices in type-II superconductors by conformal
crystal arrays.
Phys. Rev. Lett. 110,
267001 (2013).
- [21]
-
Latimer, M. L.,
Berdiyorov, G. R.,
Xiao, Z. L.,
Peeters, F. M. &
Kwok, W. K.
Realization of artificial ice systems for magnetic vortices in a superconducting MoGe
thin film with patterned nanostructures.
Phys. Rev. Lett. 111,
067001 (2013).
- [22]
-
Trastoy, J. et al.
Freezing and thawing of artificial ice by thermal switching of geometric frustration
in magnetic flux lattices.
Nat Nanotechnol. 9,
710 (2014).
- [23]
-
Ortiz-Ambriz, A. &
Tierno, P.
Engineering of frustration in colloidal artificial ices realized on
microfeatured grooved lattices.
Nat. Commun. 7
(2016).
- [24]
-
Loehr, J.,
Ortiz-Ambriz, A. &
Tierno, P.
Defect dynamics in artificial colloidal ice: real-time observation, manipulation, and logic
gate.
Phys. Rev. Lett. 117,
168001 (2016).
- [25]
-
Heyderman L. &
Stamps, R.
Artificial ferroic systems: novel functionality from structure,
interactions and dynamics.
J. Phys.: Condens. Matter
25, 363201
(2013).
- [26]
-
Gilbert, I.,
Nisoli, C. &
Schiffer, P.
Frustration by design.
Phys. Today 69,
54-59 (2016).
- [27]
-
Gilbert, I. et al.
Emergent reduced dimensionality by vertex frustration in artificial spin ice.
Nat. Phys. 12,
162 (2016).
- [28]
-
Gilbert, I. et al.
Emergent ice rule and magnetic charge screening from vertex frustration
in artificial spin ice.
Nat. Phys. 10,
670 (2014).
- [29]
-
Morrison, M. J.,
Nelson, T. R. &
Nisoli, C.
Unhappy vertices in artificial spin ice: new degeneracies from vertex
frustration.
New J. Phys. 15,
045009 (2013).
- [30]
-
Chern, G.-W.,
Morrison, M. J. &
Nisoli, C.
Degeneracy and criticality from emergent frustration in artificial spin ice.
Phys. Rev. Lett. 111,
177201 (2013).
- [31]
-
Drisko, J.,
Marsh, T. &
Cumings, J.
Topological frustration of artificial spin ice.
Nat. Commun. 8
(2017).
- [32]
-
Chern, G.-W. &
Mellado, P.
Magnetic monopole polarons in artificial spin ices.
EPL 114,
37004 (2016).
- [33]
-
Zhang, S. et al.
Crystallites of magnetic charges in artificial spin ice.
Nature 500,
553-557 (2013).
- [34]
-
Kapaklis, V. et al.
Thermal fluctuations in artificial spin ice.
Nat. Nanotechnol. 9,
514 (2014).
- [35]
-
Anghinolfi, L. et al.
Thermodynamic phase transitions in a frustrated magnetic metamaterial.
Nat. Commun. 6
(2015).
- [36]
-
Farhan, A. et al.
Exploring hyper-cubic energy landscapes in thermally active finite
artificial spin-ice systems.
Nat. Phys. 9, 375-382 (2013).
- [37]
-
Mahault, B.,
Saxena, A. &
Nisoli, C.
Emergent inequality and self-organized social classes in a network of
power and frustration.
PLoS ONE 12,
e0171832 (2017).
- [38]
-
Castelnovo, C.,
Moessner, R. &
Sondhi, S. L.
Magnetic monopoles in spin ice.
Nature 451, 42-45
(2008).
- [39]
-
Ryzhkin, I.
On magnetic relaxation in rare earth metal perchlorate metals.
Zh. Ehksperimental'noj i Teor. Fiz.
128, 559 (2005).
- [40]
-
Giblin, S. R.,
Bramwell, S. T.,
Holdsworth, P. C. W.,
Prabhakaran, D. &
Terry, I.
Creation and measurement of long-lived magnetic monopole currents in spin ice.
Nat. Phys. 7,
252 (2011).
- [41]
-
Zhang, S. et al.
Crystallites of magnetic charges in artificial spin ice.
Nature 500,
553 (2013).
- [42]
-
Drisko, J.,
Daunheimer, S. &
Cumings, J.
FePd
3 as a material for studying thermally active artificial spin ice systems.
Phys.l Rev. B 91,
224406 (2015).
- [43]
-
Castelnovo, C.
Moessner, R. &
Sondhi, S.
Thermal quenches in spin ice.
Phys. Rev. Lett. 104,
107201 (2010).
- [44]
-
Möller G. &
Moessner, R.
Magnetic multipole analysis of kagome and artificial spin-ice dipolar arrays.
Phys. Rev. B 80,
140409 (2009).
- [45]
-
Li, J. et al.
Comparing frustrated and unfrustrated clusters of single-domain ferromagnetic islands.
Phys. Rev. B 82,
134407 (2010).
- [46]
-
Nisoli, C.
Dumping topological charges on neighbors: ice manifolds for colloids and
vortices.
New J. Phys. 16, 113049
(2014).
- [47]
-
Nisoli, C.
Unexpected phenomenology in particle-based ice absent in magnetic spin ice.
Phys. Rev. Lett. 120,
167205 (2018).
- [48]
-
Libál, A.
Nisoli, C.
Reichhardt, C. J. O. &
Reichhardt, C.
Inner phases of colloidal hexagonal spin ice.
Phys. Rev. Lett. 120,
027204 (2018).
- [49]
-
Haji-Akbari, A.
Haji-Akbari, N. &
Ziff, R. M.
Dimer covering and percolation frustration.
Phys. Rev. E 92,
032134 (2015).
- [50]
-
Henley, C. L.
The "Coulomb phase" in frustrated systems.
Annu. Rev. Condens. Matter Phys.
1, 179 (2010).
- [51]
-
Castelnovo C. &
Chamon, C.
Topological ordering and topological entropy in classical systems.
Phys. Rev. B 76,
174416 (2007).
- [52]
-
Castelnovo, C.,
Moessner, R. &
Sondhi, S.
Spin ice, fractionalization, and topological order.
Annu. Rev. Condens. Matter Phys.
3, 35 (2012).
- [53]
-
Nash, L. M. et al.
Topological mechanics of gyroscopic metamaterials.
Proc. Natl. Acad. Sci. (USA) 112, 14495
(2015).
- [54]
-
Senyuk, B. et al.
Topological colloids.
Nature
493, 200 (2013).
- [55]
-
Loehr, J. et al.
Colloidal topological insulators.
Commun. Phys.
1, 4 (2018).
- [56]
-
Lieb, E. H.
Residual entropy of square ice.
Phys. Rev. 162,
162 (1967).
- [57]
-
Lieb, E. H.
Exact solution of the F model of an antiferroelectric.
Phys. Rev. Lett. 18,
1046 (1967).
- [58]
-
Bramwell S. T. &
Gingras, M. J. P.
Spin ice state in frustrated magnetic pyrochlore materials.
Science 294,
1495 (2001).
File translated from
TEX
by
TTHgold,
version 4.00.
Back to Home
| 

