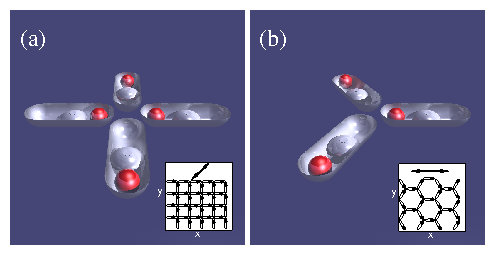
 Figure 10:
Black circles: particle locations; open ellipses: trap locations for a
20a0 ×20a0 section of a modified square ice system
with fr1=1.0, fr2=2.0, and q2=0.4. The two
trap sublattices are indicated by ellipses of different sizes. Colored
circles indicate vertex types: N0 (blue), N1 (green),
biased N2b (yellow),
ground state N2gs (gray), N3 (orange), and N4 (red).
(a) The ordered monopole state. (b) The biased triple state.
(c) The thermally induced biased ice rule obeying state.
(e) The thermally induced ground state. (f) The
paramagnetic or uncorrelated state.
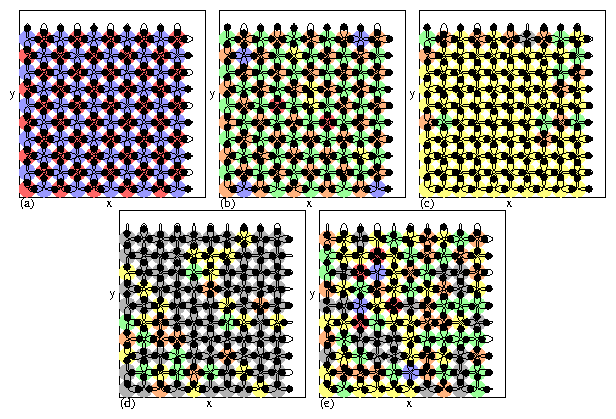
Figure 10:
Black circles: particle locations; open ellipses: trap locations for a
20a0 ×20a0 section of a modified square ice system
with fr1=1.0, fr2=2.0, and q2=0.4. The two
trap sublattices are indicated by ellipses of different sizes. Colored
circles indicate vertex types: N0 (blue), N1 (green),
biased N2b (yellow),
ground state N2gs (gray), N3 (orange), and N4 (red).
(a) The ordered monopole state. (b) The biased triple state.
(c) The thermally induced biased ice rule obeying state.
(e) The thermally induced ground state. (f) The
paramagnetic or uncorrelated state.
|