Soft Matter 12, 8606 (2016)

Collective Ratchet Effects and Reversals for Active Matter Particles on Quasi-One-Dimensional Asymmetric Substrates

Danielle McDermott^ab, Cynthia J. Olson Reichhardt^*a and Charles Reichhardt^a

^aTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: cjrx@lanl.gov; Fax: +1 505 606 0917; Tel: +1 505 665 1134
^bDepartment of Physics, Wabash College, Crawfordsville, Indiana 47933, USA

DOI: 10.1039/c6sm01394e

www.rsc.org/softmatter

Using computer simulations, we study a two-dimensional system of sterically interacting self-mobile run-and-tumble disk-shaped particles with an underlying periodic quasi-one-dimensional asymmetric substrate, and show that a rich variety of collective active ratchet behaviors arise as a function of particle density, activity, substrate period, and the maximum force exerted by the substrate. The net dc drift, or ratchet transport flux, is nonmonotonic since it increases with increased activity but is diminished by the onset of self-clustering of the active particles. Increasing the particle density decreases the ratchet transport flux for shallow substrates but increases the ratchet transport flux for deep substrates due to collective hopping events. At the highest particle densities, the ratchet motion is destroyed by a self-jamming effect. We show that it is possible to realize reversals of the direction of the net dc drift in the deep substrate limit when multiple rows of active particles can be confined in each substrate minimum, permitting emergent particle-like excitations to appear that experience an inverted effective substrate potential. We map out a phase diagram of the forward and reverse ratchet effects as a function of the particle density, activity, and substrate properties.

1 Introduction
2 Simulation and system
3 Results
4 Summary
References

Introduction

1 Introduction

A nonequilibrium assembly of particles subjected to a driving force that, by itself, produces no net motion can exhibit a net dc drift called a ratchet effect when enough symmetries are broken, such as by the introduction of an asymmetric substrate. A wide variety of ratchet effects are possible, including a rocking ratchet for particles driven over an asymmetric substrate by an ac force, or a flashing ratchet for thermally fluctuating particles interacting with a substrate that is switched on and off periodically [1,2,3]. Ratchet effects produced using asymmetric substrates have been studied in a wide range of systems including colloidal particles [4], vortices in type-II superconductors [5,6], magnetic domain walls [7,8], polymers [9,10], granular matter [11,12], and cold atoms [13]. Systems with symmetric substrates can also exhibit ratchet effects if additional asymmetry is introduced, such as from an asymmetric external driving force [14,15,16,17] or temporally asymmetric noise [18]. On an asymmetric substrate, the direction of motion in which the particles experience the smallest substrate force impeding their motion is called the easy flow direction, while the direction in which the substrate force impeding the particle motion is largest is called the hard flow direction. For overdamped non-interacting particles on an asymmetric substrate, the normal rocking ratchet effect creates a particle drift in the easy flow direction. Interacting particle systems can exhibit a reversal, or even multiple reversals, of the ratchet effect in which the net drift occurs along the hard flow direction instead [19]. Ratchet reversals have been observed in rocking ratchets for interacting superconducting vortices in asymmetric pinning arrays as a function of vortex density or ac drive amplitude [20,21,22,23,24]. While in these systems some form of external driving must be applied to produce the ratchet effect, for self-propelled particles, known as active matter [25,26,27], ratchet effects can appear in the absence of external driving [28,29,30,31,32].

Rectification effects in active matter systems were first observed for run-and-tumble swimming bacteria moving through an array of funnel-shaped barriers [28]. The initially uniformly distributed bacteria become concentrated on the easy flow side of the funnels over time, while non-swimming bacteria undergo no rectification [28]. Subsequent simulations of run-and-tumble particles in similar funnel geometries produced a similar ratchet effect caused by the interaction of the running particles with the asymmetric funnel walls, while the ratchet effect disappeared in the Brownian limit of very short running times [29]. Further studies showed that this rectification effect depends on the nature of the particle interactions with the barriers; a ratchet effect can occur when detailed balance is broken, but is absent when the particles scatter elastically from the barriers [30]. Active ratchets have been studied for a variety of self-driven systems in the presence of asymmetric substrates [33,34,35,36] or asymmetric obstacles [37,38,39], as well as for more complicated self-driven systems such as active ellipsoids [40], active polymers [41], and self-driven Janus particles [42] on asymmetric substrates. Other studies have shown how active ratchet effects can be exploited to transport non-active colloidal cargo [43], rotate asymmetric gears immersed in active matter [44,45], capture active particles with asymmetric traps [46], and direct the motion of asymmetric obstacles in active matter baths [47,48].

Fig. 1: (a) Top view of a portion of the asymmetric potential U(x), where red (blue) shading indicates high (low) potential energy. The gray circles schematically show the locations of the self-propelled particles. (b) The corresponding shape of the potential U(x) vs x.

When interactions between active matter particles are included, dynamical effects such as self-trapping [49] and self-clustering effects [50,51,52,53] arise even in the absence of a substrate. Self-clustering refers to the situation in which active particles form a large dense region even in the absence of an external potential or any attractive particle-particle interactions [54,55,56]. Recent simulations of disk-shaped active particles driven through an array of disordered obstacles show that the drift velocity of the particles initially increases with increasing activity, but decreases with increasing activity once self-clustering or self-jamming begins to occur [57]. It might be expected that active matter ratchet effects would generally diminish when particle-particle interactions are introduced, as observed by Wan et al. for run-and-tumble particles moving through a funnel array, where the ratchet effect decreased with increasing particle density [29]. This is, however, not always the case. For active matter particles on asymmetric substrates, reversals in the ratchet effect have been observed for interacting particles obeying a flocking or Vicsek model [58] that move through an array of funnel barriers [59] as well as in experiments on eukaryotic cells crawling through asymmetric channels [60]. A ratchet reversal can be exploited as a sorting mechanism if the operating parameters of the system are adjusted such that one species of particle undergoes ratcheting motion in the easy flow direction while another species undergoes ratcheting in the hard flow direction, permitting spatial separation. For simpler systems such as self-propelled disks or rods on asymmetric substrates, ratchet reversals have not yet been observed.

In this work we examine a two-dimensional (2D) system of sterically interacting run-and-tumble disk-shaped particles moving over an asymmetric quasi-one-dimensional periodic substrate. We find that at low particle densities, a ratchet effect occurs in the easy flow direction of the substrate asymmetry. For shallow substrates, the ratchet transport flux increases with increasing run time, and it decreases with increasing particle density when self-clustering occurs. For deep substrates, the ratchet transport flux is a nonmonotonic function of particle density and run time. When the substrate is deep enough to confine multiple rows of particles in each potential minimum, multibody collisions can occur that push particles over the substrate barriers, generating a reversed ratchet effect with motion in the hard flow direction of the substrate asymmetry. This reversed ratchet effect is suppressed at high particle densities when self-clustering occurs, and it also disappears for very deep substrates when the particles form one-dimensional rows in which multibody collisions do not occur. A transition from a reverse to a normal ratchet effect can occur when the run time is increased. We describe the direction and transport flux of the ratchet effect in a series of phase diagrams as functions of the particle density, run time, substrate periodicity, and the maximum force exerted by the substrate. Possible physical systems in which such effects could be observed include swarm robots moving over a landscape or artificial swimmers confined to 2D and interacting with a substrate of optical traps [61,62,63] or an asymmetrically corrugated surface.

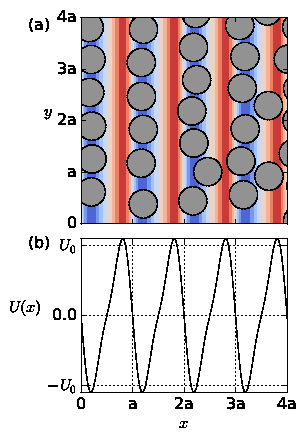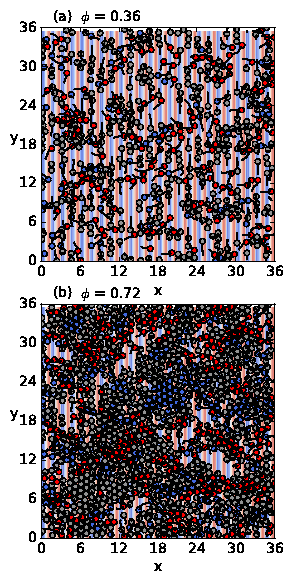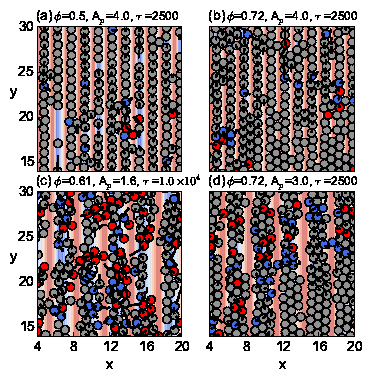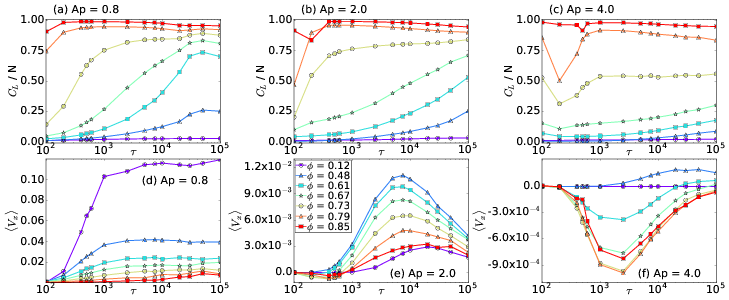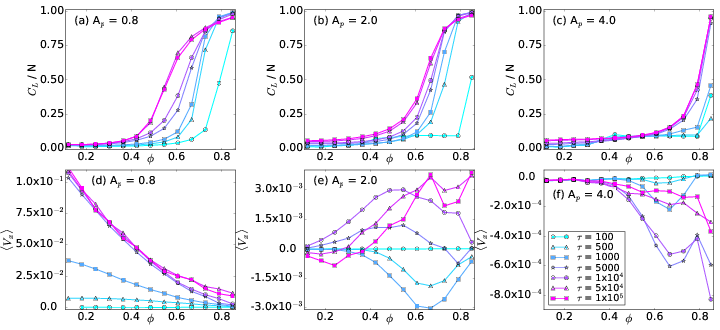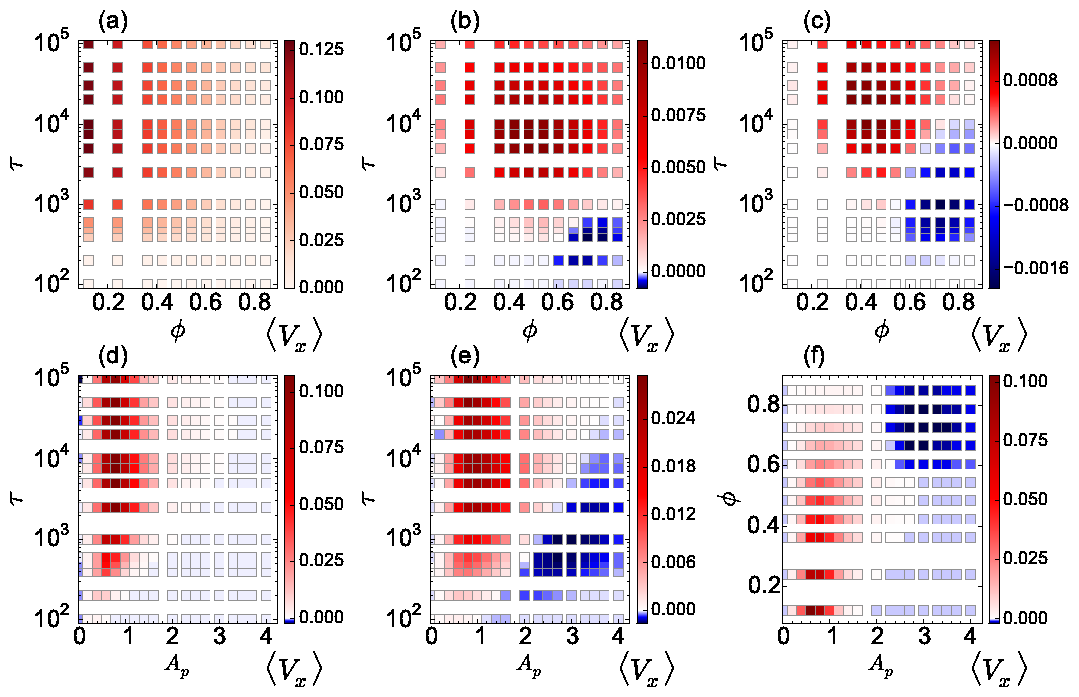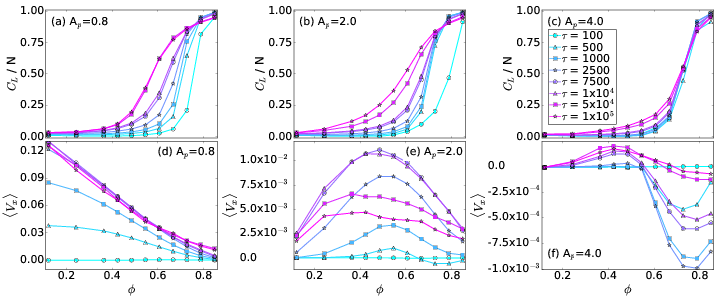
Fig. 2: (a,b,c) The average cluster size C_L/N vs particle density ϕ. (d,e,f) The average particle velocity 〈V_x 〉 vs ϕ. The color code, shown in panel (f), indicates different run times τ = 100, 500, 1000, 2500, 7500, 1×10⁴, 5×10⁴, and 1×10⁵. (a,d) At A_p = 0.8, there is a normal ratchet effect with a transport flux that decreases with increasing ϕ. (b,e) At A_p = 2.0, the transport flux of the normal ratchet effect is nonmonotonic, so that the ratcheting is optimized for a midrange value of ϕ. (c,f) At A_p = 4.0, there is a crossover from a normal to a reverse ratchet effect with increasing ϕ.

2 Simulation and system

We consider a 2D system of size L ×L with periodic boundary conditions in the x- and y-directions containing N self-propelled disk-shaped particles. The steric particle-particle interactions are modeled as a harmonic repulsive potential which drops to zero beyond the particle radius r_d. We take r_d = 0.5 and L = 36 in dimensionless simulation length units. The particle density ϕ is given by the total fraction of the sample area covered by the particles, ϕ = Nπr²_d/L². The highest possible particle density in 2D is a triangular solid with ϕ = 0.9. The dynamics of a particle i is governed by the following overdamped equation of motion:

d r_i

= F_i^m + Fⁱⁿ_i + F^sub_i .

(1)

Here η is the damping constant, which is set equal to unity. We use dimensionless simulation units, in which distance is measured in terms of a₀, force is measured in terms of F₀, velocity is measured in terms of F₀/η, and time is measured in terms of a₀η/F₀. We use a Verlet algorithm to integrate the equations of motion, and we neglect thermal fluctuations. The self-propulsion is modeled using run-and-tumble dynamics in which the motor force F_i^m is fixed to a randomly chosen direction during a running time τ, after which a new randomly chosen direction is selected for the next running time τ. We take the magnitude of the motor force to be fixed at F_m=1.0. The running direction is selected from a uniform probability distribution, and the running time is always equal to the value of τ. In the absence of any other interactions, during a single run interval a particle travels a distance R_l = F_mτ∆t, where ∆t=0.002 is the size of the simulation time step. Each particle contains a "clock" that determines when the next tumbling event should occur, and these clocks are initialized randomly over the interval [0,τ] so that the particles do not all tumble simultaneously. The steric particle-particle interaction force is Fⁱⁿ_i = ∑^N_{i ≠ j}k(2r_d − |r_ij|)Θ(2r_d − |r_ij|)∧r_ij where r_ij=r_i−r_j, ∧r_ij=r_ij/|r_ij|, Θ is the Heaviside step function, and the spring constant k=30. This force produces the disk shape of the particle as it extends to a maximum distance of r_d from the center of the particle. The initial positions of the particles are chosen randomly with the constraint that particle overlap is forbidden. The substrate force F_i^sub = −∇U(x_i)∧x arises from an asymmetric potential of the form

U(x) = −U₀[sin(2πx/a) + 0.25sin(4πx/a)]

(2)

where a is the substrate period and the maximum force exerted by the substrate, which we call the substrate strength, is defined to be A_p = 2πU₀/a. Unless otherwise noted, we take a=1.5a₀=3 r_d. A small section of U(x) is illustrated in Fig. 1. To quantify the ratchet effect, we measure the net velocity per particle in the x direction, 〈V_x 〉 = N⁻¹∑_{i = 1}^N v_i·∧x, where v_i is the velocity of particle i. We average 〈V_x〉 over at least 10⁷ simulation time steps to ensure that we are obtaining a steady state measurement. The average slope of V_x(t) is constant over this time interval. We vary ϕ, A_p, a, and τ and measure the resulting direction and transport flux of the ratcheting behavior.

Fig. 3: Active particle positions (circles) and trajectories (black lines), along with the underlying substrate potential (red and blue lines), at A_p = 0.8 and τ = 10⁵ for the system in Fig. 2(a,d). Red particles have moved a distance ∆x ≥ a/4 in the forward (positive x) direction during the illustrated time interval, while blue particles have moved a distance ∆x ≥ a/4 in the reverse (negative x) direction; gray particles have moved a distance ∆x < a/4. (a) At ϕ = 0.36, there is a large normal ratchet effect and few clusters are present. (b) At ϕ = 0.72, self-cluster formation suppresses the ratchet effect.

3 Results

We first demonstrate that as the substrate strength increases, the system transitions from a forward to a reverse ratchet effect. In Fig. 2(a) we plot the normalized size of the largest particle cluster C_L/N versus ϕ for varied run times τ at a fixed substrate strength of A_p = 0.8. A group of n particles that are all in physical contact with each other is defined to be a cluster of size C_L=n. We measure C_L using the algorithm described in ref. 64, and define the system to be in a self-clustering state when C_L/N > 0.5. As τ increases, the onset of self-clustering shifts to lower values of ϕ, in agreement with earlier studies showing that self-clustering occurs at lower densities when the run time [57] or the persistence length [50,51] of the motor force is increased. Figure 2(d) shows the corresponding values of 〈V_x 〉 versus ϕ. For the lowest value of τ = 100, corresponding to R_l=0.4r_d, the system is in the Brownian limit and 〈V_x 〉 = 0 for all values of ϕ, while at higher run times, the system exhibits a normal ratchet effect. In this shallow substrate regime, we find that 〈V_x 〉 decreases with increasing ϕ and increases with increasing τ, with a saturation for τ > 7500 as shown in Fig. 2(d). This result is in agreement with the studies of Wan et al. on interacting active particles in funnel arrays, where the magnitude of the ratchet effect increases with increasing τ before reaching a plateau at large τ, and decreases with increasing particle density [29]. For the shallow substrate system in Fig. 2(a,d), at low ϕ very few particle-particle collisions occur, making the behavior similar to that of a single particle, which moves further along the easy flow direction of the substrate asymmetry than along the hard flow direction since F^m > A_p. As ϕ increases, two effects combine to reduce the magnitude of the forward ratchet effect. The particles collide more often, producing a more thermal distribution of particle motion, while individual particles are more likely to become trapped inside a cluster, therefore becoming unavailable for hopping over the substrate barrier.

Fig. 4: Active particle positions (circles) and trajectories (black lines), along with the underlying substrate potential (red and blue lines), in a portion of the sample for the system in Fig. 2(b,e) with A_p = 2.0. Particles are colored as in Fig. 3. (a) At ϕ = 0.24 and τ = 100, 〈V_x 〉 = 0 and the particles are trapped in the substrate minima. (b) At ϕ = 0.72 and τ = 100, a uniform pinned state forms with 〈V_x 〉 = 0. (c) At ϕ = 0.72 and τ = 2500, a normal ratchet effect occurs. (d) At ϕ = 0.72 and τ = 1×10⁵, the occurrence of self-clustering reduces the magnitude of the normal ratchet effect.

In Fig. 3 we show the particle positions and trajectories for the shallow substrate system from Fig. 2(a,d) with A_p=0.8 at τ = 10⁵. At ϕ = 0.36, there is a large normal ratchet effect and Fig. 3(a) shows that few clusters are present. Particles that have moved a distance ∆x ≥ a/4 in the easy (positive x) flow direction are colored red, while those that have moved a distance ∆x ≥ a/4 in the hard (negative x) flow direction are colored blue. As indicated in Fig. 3(a), particles are frequently able to hop over the substrate barriers, and due to the substrate asymmetry, hops in the easy flow direction occur more often than hops in the hard flow direction, leading to a net normal ratchet effect. At ϕ = 0.72, shown in Fig. 3(b), strong self-clustering is present and the normal ratchet effect is much weaker. Due to the self-clustering, the particles tend to move collectively at this density, and large regions of the system become jammed, with particles unable to hop over substrate barriers in either direction. The high particle density also tends to nullify the effectiveness of the substrate asymmetry, so that the few particles that are still able to hop over barriers have a nearly equal probability of hopping in the easy flow direction as in the hard flow direction, destroying the ratchet effect.

Fig. 5: Active particle positions (circles) and trajectories (black lines), along with the underlying substrate potential (red and blue lines), in a portion of the sample. Particles are colored as in Fig. 3. (a) For A_p=4.0, ϕ = 0.5, a=3 r_d, and τ = 2500, the particles form one-dimensional chains in each substrate minimum and there is a weak normal ratchet effect. (b) At A_p=4.0, ϕ = 0.72, a=3 r_d, and τ = 2500, each substrate minimum contains one full row of particles along with a partial second row, and a reverse ratchet effect occurs. (c) Normal ratcheting motion for A_p=1.6, ϕ = 0.61, a=6 r_d, and τ = 1×10⁴. (d) Reverse ratcheting motion for A_p=3.0, ϕ = 0.72, a=6 r_d, and τ = 2500.

In Fig. 2(b,e) we plot C_L/N and 〈V_x 〉 versus ϕ at a higher substrate strength of A_p = 2.0 for varied τ. We again find that C_L/N increases with increasing ϕ and that the onset of self-clustering drops to lower values of ϕ as τ increases. For the lowest value of τ, 〈V_x〉 = 0, and the maximum value of 〈V_x 〉 increases with increasing τ up to a saturation value of τ = 7500, above which it decreases with increasing τ, indicating that there is a run time that optimizes the ratchet transport flux. We note that the forward ratchet motion has decreased by an order of magnitude compared to its value at small substrate strength. As a function of ϕ, 〈V_x 〉 is nonmonotonic, starting from a low value in the single particle limit at low ϕ, and then increasing to a maximum value at the optimum density of ϕ^*=0.55 before decreasing again. The value of ϕ^* shifts to slightly lower densities as τ increases. The nonmonotonic behavior of 〈V_x〉 arises due to a competition between different collective effects. Since A_p > F^m, isolated particles cannot hop over the substrate barriers in either direction, so that 〈V_x〉 = 0 at low ϕ in the single particle limit. As ϕ increases, the increased chance for collisions permits a collective barrier hopping process to occur in which interactions between multiple particles permit at least one of the particles to hop over a substrate barrier, preferentially in the easy flow direction of the substrate asymmetry. For A_p ≤ F^m, interactions between pairs of particles is enough to permit motion in the easy flow direction to occur, but for A_p > F^m, three-body collisions are required to push at least one particle into a neighboring substrate minimum, preferentially on the easy flow direction side. At low density the three-body interactions cannot occur and there is no ratcheting effect, but as ϕ increases the magnitude of the normal ratchet effect increases up to ϕ ≈ 0.5. Above this density, the particle-particle interactions overwhelm the substrate asymmetry as described above for the A_p=0.8 case, bringing the rate of forward hopping down until it equals the rate of backward hopping and the ratchet effect is lost.

Fig. 6: (a,b,c) C_L/N vs τ and (d,e,f) 〈V_x〉 vs τ for ϕ = 0.12, 0.48, 0.61, 0.67, 0.73, 0.79, and 0.85. (a,d) A_p = 0.8. (b,e) A_p = 2.0. (c,f) A_p = 4.0, where a reverse ratchet effect can occur.

In Fig. 4 we show the particles and trajectories for the system in Fig. 2(b,e) with A_p=2.0. At ϕ = 0.24 and τ = 100, shown in Fig. 4(a), the particles remain confined in the substrate potential minima and 〈V_x〉 = 0. At ϕ = 0.72 and τ = 100, shown in Fig. 4(b), we still find 〈V_x 〉 = 0, and the particles form a uniform pinned state. When self-clustering first begins at ϕ = 0.72 for τ = 2500, there is a normal ratchet effect illustrated in Fig. 4(c), while for ϕ = 0.72 and a higher run time of τ = 1×10⁵, Fig. 4(d) indicates that large numbers of clusters form in the system and interfere with the normal ratchet effect, reducing its magnitude.

In Fig. 2(c,f) we show C_L/N and 〈V_x 〉 versus ϕ for a variety of τ values in the deep substrate limit of A_p = 4.0. Here the C_L/N curves show little variation with τ since the arrangement of the particles is dominated by the substrate minima. At the smallest values of ϕ, the particles are strongly trapped in the substrate minima and 〈V_x 〉 = 0. For 0.2 < ϕ < 0.6, we observe a normal ratchet effect with a maximum transport flux near ϕ = 0.4. A reverse ratchet effect appears for ϕ ≥ 0.6 that is most pronounced for τ = 2500 and decreases in magnitude for larger τ. The magnitude of 〈V_x〉 in the reverse ratchet regime is very similar for A_p=2.0 and A_p=4.0 in Figs. 2(e,f), but in the forward ratchet regime 〈V_x〉 drops by an order of magnitude when A_p is large.

In Fig. 5(a) we show that at A_p=4.0, ϕ = 0.5, and τ = 2500, the particles form one-dimensional chains in each substrate minimum and a weak normal ratchet effect occurs. At ϕ = 0.72 and τ = 2500, where a reverse ratchet effect occurs, Fig. 5(b) shows that the particles have buckled out of the bottom of the substrate minima to form two partial rows of particles. The reversal of the ratchet effect as a function of ϕ occurs when the buckling of the particles in the substrate potential causes particle-particle interactions instead of particle-substrate interactions to dominate the particle motion. When the substrate is deep, for low ϕ each substrate minimum captures a single row of particles. Although isolated particles show no ratcheting behavior, when pairs of particles can come into contact along the y direction, one member of the pair can escape into a neighboring substrate minimum, preferentially on the easy flow direction side, producing a weak normal ratchet effect. For ϕ ≥ 0.5, a single row of particles can no longer fit in each substrate minima, and the particles buckle to form one nearly complete row and a second partial row. The nearly complete row rests on the hard flow side of the substrate minimum since this provides a stronger confinement, while the partial row rests on the easy flow side of the substrate minimum. The effective asymmetry of the potential is reversed since the difference in slopes on the hard flow and easy flow sides of the substrate minimum becomes unimportant at these high densities, and instead, the physical distance to the substrate maximum becomes the dominant effect. The maximum is closer to the minimum in the hard flow direction than in the easy flow direction, so hopping in the hard flow direction is favored at large ϕ, producing a reverse ratchet effect. As ϕ is further increased, the substrate minimum becomes filled with particles and the asymmetry in the distance to the substrate maximum becomes less important in determining the hopping direction, causing a decrease in the transport flux of the reverse ratchet, as shown in Fig. 2(f) for ϕ > 0.7. Similarly, the reverse ratchet effect becomes very weak at large values of τ when the local asymmetry in the distance to the substrate maximum becomes unimportant.

Fig. 7: (a) C_L/N vs τ and (d) 〈V_x 〉 vs τ for ϕ = 0.12, 0.48, 0.61, 0.67, 0.73, 0.79, and 0.85 at A_p=2.5, where there can be a transition from a reverse ratchet to a normal ratchet with increasing τ. (b,e) C_L/N and 〈V_x 〉 vs A_p at ϕ = 0.36 for τ = 100, 500, 1000, 2500, 7500, 1×10⁴, 5×10⁴, and 1×10⁵, showing that only a normal ratchet effect occurs. (c,f) C_L/N and 〈V_x 〉 vs A_p at ϕ = 0.61 for the same τ values as in panels (b) and (e). Inset of (f): blow up of main panel showing a detail of the weak reverse ratchet effect that appears at large A_p.

In Fig. 6 we show C_L/N and 〈V_x 〉 as a function of τ for varied ϕ at different substrate strengths. At A_p=0.8 in Fig. 6(a), C_L/N increases with increasing τ at low ϕ but saturates to C_L/N ≈ 1.0 at high ϕ. In Fig. 6(d), the corresponding 〈V_x 〉 curves increase with increasing τ up to a plateau, while the average value of 〈V_x〉 drops as ϕ increases, indicating that for shallow substrates with 0 < A_p < 1.0, self-clustering suppresses the normal ratchet effect by nullifying the substrate asymmetry. At A_p=2.0 in Fig. 6(e), 〈V_x 〉 is nonmonotonic, with a peak in the magnitude of the ratchet effect for 5000 < τ < 1×10⁴, and a decrease in 〈V_x 〉 at large values of τ due to the occurrence of self-clustering. For high densities of ϕ > 0.67, there is a window at small τ in which a reverse ratchet effect appears caused by particles hopping over the closest maximum instead of traveling up the least steep side of the potential. Figure 6(c,f) shows C_L/N and 〈V_x 〉 versus τ for A_p = 4.0. There is a normal ratchet effect at large τ for ϕ < 0.5 and a reverse ratchet effect at intermediate τ for ϕ ≥ 0.5. The transport flux of the reverse ratchet is highest at τ ≈ 5000, but its absolute value is still an order of magnitude smaller than that of the normal ratchet effect.

For substrate strengths of 1.6 < A_p < 4.0, a crossover from a reverse to a normal ratchet effect can occur as a function of τ, as highlighted in Fig. 7(a,d), where we plot C_L/N and 〈V_x 〉 versus τ for a sample with A_p=2.5. There is a clear transition from a reverse ratchet to a normal ratchet effect with increasing τ, suggesting that in a system composed of two species of particles with different τ, it could be possible to have the two species exhibit a net drift in opposite directions.

Fig. 8: (a,b,c) C_L/N vs τ and (d,e,f) 〈V_x 〉 vs ϕ for τ = 100, 500, 1000, 5000, 1×10⁴, 5×10⁴, and 1×10⁵ in samples with a substrate lattice constant of a=6 r_d, twice as large as the lattice constant considered previously. (a,d) A_p = 0.8. (b,e) At A_p=2.0 a reverse ratchet effect occurs. (c,f) At A_p=4.0, the magnitude of the reverse ratchet effect initially increases with increasing τ for τ < 1×10⁴ and then decreases as τ further increases.

Fig. 9: Phase diagrams in samples with a=3 r_d showing the magnitude of the ratchet effect as determined by the value of 〈V_x〉, with blue denoting a reverse ratchet and red denoting a normal ratchet, as indicated by the color bar keys. (a,b,c) τ vs ϕ phase diagrams at (a) A_p = 0.8, (b) A_p = 2.0, and (c) A_p = 3.0. (d,e) τ vs A_p phase diagrams at (d) ϕ = 0.24 and (e) ϕ = 0.68. (f) ϕ vs A_p phase diagram at τ = 1000.

In Fig. 7(b,e) we show C_L/N and 〈V_x 〉 versus A_p for varied τ at ϕ = 0.36, while in Fig. 7(c,f) we show the same measures at ϕ = 0.61. In Fig. 7(b) at ϕ = 0.36, the particle density is too low for large clusters to appear, while in Fig. 7(c) at ϕ = 0.61, the self-clustering that occurs for low A_p is suppressed as the substrate strength is increased. At A_p=0 in Fig. 7(e,f), 〈V_x 〉 = 0, and as A_p increases, 〈V_x〉 increases to a maximum value near A_p=0.75 before decreasing back to zero at higher A_p. The normal ratchet effect operates most effectively when particles can overcome only the barrier for motion in the easy flow direction, and not the barrier in the hard flow direction. The particles can overcome the barrier in the easy flow direction when A_p ≤ A_p^e with A_p^e=(3/2)F^m, and they can overcome the barrier in the hard flow direction when A_p ≤ A_p^h with A_p^h=(3/4)F^m. Thus, the ratchet effect is zero for large A_p, becomes finite below A_p = A_p^e = 1.5, and diminishes rapidly below A_p ≈ A_p^h=0.75. In Fig. 7(c,f) at ϕ = 0.61, increasing A_p decreases the cluster size C_L/N for τ < 7.5×10⁴ as the particles become increasingly localized, while at τ = 1×10⁵, C_L/N develops a small nonmonotonic peak near A_p=1.5. For all τ, there is still a local maximum in 〈V_x 〉 near A_p ≈ 0.75, while for A_p > 2.0 at low values of τ, a weak reverse ratchet effect occurs

We have also examined systems with different substrate periods a. We find that for larger values of a, the onset of the formation of multiple rows of particles in a single substrate minimum shifts to lower ϕ, and that therefore the reverse ratchet regime increases in extent. In Fig. 8(a,d) we show C_L/N and 〈V_x 〉 versus ϕ at A_p = 0.8 for varied τ in a sample with a=6 r_d, twice as large as the lattice constant considered previously. For A_p < 1.0, there is a normal ratchet effect that generally decreases in magnitude with increasing ϕ and that saturates in magnitude with increasing τ. In Fig. 8(b,e), we plot the same quantities for A_p = 2.0, where the ratchet effect becomes nonmonotonic and switches from a reverse ratchet for τ < 5000 to a normal ratchet for τ ≥ 5000. In contrast, for the a=3 r_d system in Fig. 3 at the same value of A_p, there is almost no reverse ratchet regime. In Fig. 8(c,f), the C_L/N and 〈V_x〉 versus ϕ curves for a=6 r_d at A_p = 4.0 indicate that the ratchet effect is always in the reverse direction with a magnitude that increases with increasing ϕ, a behavior that is the opposite of that observed at A_p = 0.8.

Fig. 10: Phase diagrams as a function of τ vs ϕ showing the magnitude of the ratchet effect as determined by the value of 〈V_x〉, with blue denoting a reverse ratchet and red denoting a normal ratchet, as indicated by the color bar keys. (a) At A_p = 1.6 and a = 3 r_d, there is a normal ratchet effect. (b) At A_p=1.6 and a=6 r_d, there is a transition from a normal to a reverse ratchet effect. (c) At A_p = 3.0 and a = 4 r_d, the reverse ratchet regime extends to higher values of τ. (d) At A_p=3.0 and a = 6 r_d, the ratchet effect is predominately in the reverse direction.

In Fig. 9 we highlight the different ratcheting behaviors for a=3 r_d in a series of phase diagrams colored according to the value of 〈V_x 〉, where blue indicates a reverse ratchet effect, white indicates no ratchet effect, and red indicates a normal ratchet effect. In Fig. 9(a) we show a τ versus ϕ phase diagram at A_p = 0.8 where only a normal ratchet effect occurs. The ratchet transport flux decreases with decreasing τ and increasing ϕ. At A_p=2.0 in Fig. 9(b), the τ versus ϕ phase diagram plot indicates that the maximum normal ratchet effect appears near ϕ = 0.5 and τ = 10⁴, while small reverse ratchet effects appear in the lower right hand corner at low τ and large ϕ. In Fig. 9(c), the τ versus ϕ phase diagram shows that the extent of the reversed ratchet regime is larger and that there is a clear transition from a reverse to a normal ratchet as a function of increasing τ and/or decreasing ϕ. As A_p is further increased, the reversed ratchet region grows, but the magnitude of the ratchet effect is generally reduced. In the τ versus A_p phase diagram at ϕ = 0.24 in Fig. 9(d), the ratchet effect is always in the normal direction and is maximum in a band along the A_p = 0.8 line. Regions of normal and reverse ratcheting appear in the τ versus A_p phase diagram for ϕ = 0.68, as shown in Fig. 9(e). In the ϕ versus A_p phase diagram for fixed τ = 1000 in Fig. 9(f), a normal ratchet effect occurs for A_p < 2.0, while there is a transition to a reverse ratchet effect for A_p > 2.0 and ϕ > 0.5.

In Fig. 10(a) we show the ratchet phase diagram as a function of τ versus ϕ for a system with A_p = 1.6 and a = 3 r_d, where the ratchet effect is always in the normal direction. For A_p=1.6 and a=6 r_d in Fig. 10(b), at large τ a normal ratchet effect occurs, as shown in Fig. 5(c) for ϕ = 0.61 and τ = 1 ×10⁴, while at lower τ, multiple rows of particles can be trapped in each substrate minimum, producing a region of reverse ratchet effect. At higher values of A_p, the size of the reverse ratchet effect region increases, as shown in Fig. 10(c) for A_p = 3.0 and a = 4 r_d. In Fig. 10(d) at A_p=3.0 and a=6 r_d, the ratchet effect is predominately in the reverse direction, as illustrated in Fig. 5(d) for ϕ = 0.72 and τ = 2500.

4 Summary

We show that in a 2D system of sterically interacting run-and-tumble disk-shaped particles in the presence of a quasi-one-dimensional asymmetric periodic substrate, a variety of collective active ratchet behaviors can occur, including nonmonotonic changes in the ratchet effect magnitude as well as ratchet reversals. A normal ratchet effect, where a net drift of the particles occurs along the easy flow direction of the substrate, appears for shallow substrates, and the ratchet transport flux generally decreases with increasing particle density due to self-jamming or self-clustering effects since it is more difficult for a cluster to undergo ratcheting motion than for individual particles to do so. For intermediate substrate strengths, the ratchet transport flux is nonmonotonic as function of particle density or activity. At low particle densities, individual particles cannot jump over the potential barrier, but particle-particle interactions can produce a collective particle hopping in the easy flow direction of the substrate asymmetry. When the particle density or activity is high enough, strong self-clustering effects occur that reduce the ratchet transport flux. For deep substrates where multiple rows of particles can form in each substrate minimum, it is possible to realize a reverse ratchet effect in which the net flux of particles is in the hard flow direction of the substrate asymmetry. The size of the reverse ratchet regime can be increased by increasing the size of the substrate periodicity, which shifts the transition from single to multiple rows of particles per substrate minimum to lower particle densities. Our work shows that by exploiting collective effects, it is possible to create reversible active matter ratchets which could be useful for various sorting applications.

Acknowledgements

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396. The work of DM was supported in part by the U.S. DoE, Office of Science, Office of Workforce Development for Teachers and Scientists (WDTS) under the Visiting Faculty Program (VFP).

References

[1]: P. Reimann, Phys. Rep., 2002, 361, 57.
[2]: H. Linke, Appl. Phys. A, 2002, 75, 167.
[3]: P. Hänggi and F. Marchesoni, Rev. Mod. Phys., 2009, 81, 387.
[4]: J. Rousselet, L. Salome, A. Ajdari, and J. Prost, Nature (London), 1994, 370, 446.
[5]: C.S. Lee, B. Jankó, I. Derényi, and A.L. Barabási, Nature (London), 1999, 400, 337.
[6]: J. F. Wambaugh, C. Reichhardt, C.J. Olson, F. Marchesoni, and F. Nori, Phys. Rev. Lett., 1999, 83, 5106.
[7]: A. Pérez-Junquera, V.I. Marconi, A.B. Kolton, L.M. Álvarez-Prado, Y. Souche, A. Alija, M. Vélez, J.V. Anguita, J.M. Alameda, J.I. Martín, and J.M.R. Parrondo, Phys. Rev. Lett., 2008, 100, 037203.
[8]: J.H. Franken, H.J.M. Swagten, and B. Koopmans, Nature Nanotechnol., 2012, 7, 499.
[9]: M.T. Downton, M.J. Zuckermann, E.M. Craig, M. Plischke, and H. Linke, Phys. Rev. E, 2006, 73, 011909.
[10]: M. Kenward and G. Slater, Phys. Rev. E, 2008, 78, 051806.
[11]: Z. Farkas, P. Tegzes, A. Vukics, and T. Vicsek, Phys. Rev. E, 1999, 60, 7022.
[12]: J.F. Wambaugh, C. Reichhardt, and C.J. Olson, Phys. Rev. E, 2002, 65, 031308.
[13]: P.H. Jones, M. Goonasekera, and F. Renzoni, Phys. Rev. Lett., 2004, 93, 073904.
[14]: C. Reichhardt and C.J. Olson Reichhardt, Phys. Rev. E, 2003, 68, 046102.
[15]: D. Speer, R. Eichhorn, and P. Reimann, Phys. Rev. Lett., 2009, 102, 124101.
[16]: P. Tierno and T.M. Fischer, Phys. Rev. Lett., 2014, 112, 048302.
[17]: M. Januszewski and J. Luczka, Phys. Rev. E, 2011, 83, 051117.
[18]: J. Luczka, R. Bartussek, and P. Hänggi, Europhys. Lett., 1995, 31, 431.
[19]: I. Derényi and T. Vicsek, Phys. Rev. Lett., 1995, 75, 374.
[20]: J.E. Villegas, S. Savel'ev, F. Nori, E.M. Gonzalez, J.V. Anguita, R. Garcia, and J.L. Vicent, Science, 2003, 302, 1188.
[21]: C.C. de Souza Silva, J. Van de Vondel, M. Morelle, and V.V. Moshchalkov, Nature (London), 2006, 440, 651.
[22]: V.I. Marconi, Phys. Rev. Lett., 2007, 98, 047006.
[23]: Q. Lu, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. B, 2007, 75, 054502.
[24]: D. Perez de Lara, M. Erekhinsky, E.M. Gonzalez, Y.J. Rosen, I.K. Schuller, and J.L. Vicent, Phys. Rev. B, 2011, 83, 174507.
[25]: M.C. Marchetti, J.F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, and R.A. Simha, Rev. Mod. Phys., 2013, 85, 1143.
[26]: M.E. Cates, Rep. Prog. Phys., 2012, 75, 042601.
[27]: C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, arXiv:1602.00081 (unpublished).
[28]: P. Galajda, J. Keymer, P. Chaikin, and R. Austin, J. Bacteriol., 2007, 189, 8704.
[29]: M.B. Wan, C.J. Olson Reichhardt, Z. Nussinov, and C. Reichhardt, Phys. Rev. Lett., 2008, 101, 018102.
[30]: J. Tailleur and M.E. Cates, Europhys. Lett., 2009, 86, 60002.
[31]: L. Angelani, A. Costanzo, and R. Di Leonardo, Europhys. Lett., 2011, 96, 68002.
[32]: C.J. Olson Reichhardt and C. Reichhardt, Ann. Rev. Cond. Matt. Phys. , 2017, 8, 51.
[33]: V. Kantsler, J. Dunkel, M. Polin, and R. E. Goldstein, Proc. Natl. Acad. Sci. (USA), 2013, 110, 1187.
[34]: A. Pototsky, A. M. Hahn, and H. Stark, Phys. Rev. E, 2013, 87, 042124.
[35]: B. Ai, Q. Chen, Y. He, F. Li, and W. Zhong, Phys. Rev. E, 2013, 88, 062129.
[36]: E. Yariv and O. Schnitzer, Phys. Rev. E, 2014, 90, 032115.
[37]: I. Berdakin, Y. Jeyaram, V.V. Moshchalkov, L. Venken, S. Dierckx, S.J. Vanderleyden, A.V. Silhanek, C.A. Condat, and V.I. Marconi, Phys. Rev. E, 2013, 87, 052702.
[38]: C. Reichhardt and C. J. Olson Reichhardt, Phys. Rev. E, 2013, 88, 062310.
[39]: F.Q. Potiguar, G.A. Farias, and W.P. Ferreira, Phys. Rev. E, 2014, 90, 012307.
[40]: B.-Q. Ai and J.-C. Wu, J. Chem. Phys., 2014, 140, 094103.
[41]: M.-B. Wan and Y. Jho, Soft Matter, 2013, 9, 3255.
[42]: P.K. Ghosh, V.R. Misko, F. Marchesoni, and F. Nori, Phys. Rev. Lett., 2013, 110, 268301.
[43]: N. Koumakis, A. Lepore, C. Maggi, and R. Di Leonardo, Nature Commun., 2013, 4, 2588.
[44]: R. Di Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M.P. Conte, F. Mecarini, F. De Angelis, and E. Di Fabrizio, Proc. Natl. Acad. Sci. (USA), 2010, 107, 9541.
[45]: A. Sokolov, M.M. Apodaca, B.A. Grzybowski, and I.S. Aranson, Proc. Natl. Acad. Sci. (USA), 2010, 107, 969.
[46]: A. Kaiser, K. Popowa, H.H. Wensink, and H. Löwen, Phys. Rev. E, 2013, 88, 022311.
[47]: A. Kaiser, A. Peshkov, A. Sokolov, B. ten Hagen, H. Löwen, and I.S. Aranson, Phys. Rev. Lett., 2014, 112, 158101.
[48]: S.A. Mallory, C. Valeriani, and A. Cacciuto, Phys. Rev. E, 2014, 90, 032309.
[49]: J. Tailleur and M.E. Cates, Phys. Rev. Lett., 2008, 100, 218103.
[50]: Y. Fily and M.C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702.
[51]: G.S. Redner, M.F. Hagan, and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701.
[52]: J. Palacci, S. Sacanna, A.P. Steinberg, D.J. Pine, and P.M. Chaikin, Science, 2013, 339, 936.
[53]: I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger, and T. Speck, Phys. Rev. Lett., 2013, 110, 238301.
[54]: D. Benczdi, I. Tomka, and F. Escher, Macromolecules, 1998, 31, 3062.
[55]: M.P. Magiera and L. Brendel, Phys. Rev. E, 2015, 92, 012304.
[56]: J. Schöneberg, A. Ullrich, and F. Noé, BMC Biophysics, 2014, 7, 11.
[57]: C. Reichhardt and C. J. Olson Reichhardt, Phys. Rev. E, 2014, 90, 012701.
[58]: T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226.
[59]: J.A. Drocco, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. E, 2012, 85, 056102.
[60]: G. Mahmud, C.J. Campbell, K.J.M. Bishop, Y.A. Komarova, O. Chaga, S. Soh, S. Huda, K. Kandere-Grzybowska, and B.A. Grzybowski, Nature Phys., 2009, 5, 606.
[61]: A. Chowdhury, B.J. Ackerson, and N.A. Clark, Phys. Rev. Lett., 1985, 55, 833.
[62]: Q.-H. Wei, C. Bechinger, D. Rudhardt, and P. Leiderer, Phys. Rev. Lett., 1998, 81, 2606.
[63]: L. Zaidouny, T. Bohlein, R. Roth, and C. Bechinger, Soft Matter, 2013, 9, 9230.
[64]: S. Luding and H.J. Herrmann, Chaos, 1999, 9, 673.

File translated from T_EX by T_TH, version 4.08.
Back to Home