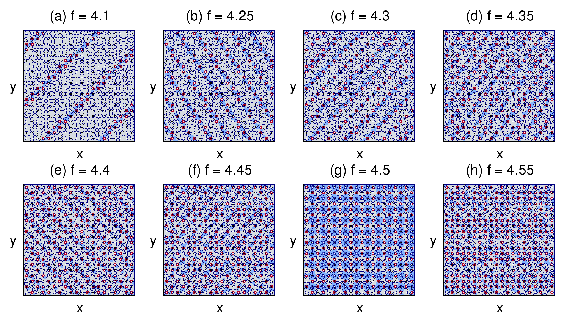
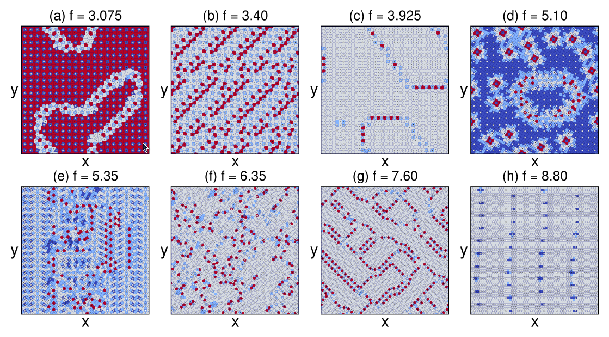
Fig. 1:
The Voronoi diagrams of the
colloidal particle configurations on a square pinning array.
Filled dots: particle locations; open circles: pinning site locations.
Polygon colors indicate the coordination number of the particle at the
center of the polygon: 4 (dark blue), 5 (light blue), 6 (grey), or 7 (red).
(a) At f=4, each pinning site captures one particle and
a hexagonal lattice forms.
(b) At f = 4.5, the particles form a superlattice
structure with a periodicity of twice the pinning lattice unit cell.
(c) At f = 5.0, a square lattice forms.
(d) A stacked percentage chart of
the fraction of particles with coordination number of 4 (dark blue), 5
(light blue), 6 (grey), and 7 (red) vs filling factor f showing how
the system evolves from a hexagonal structure at f=4 to a square
structure at f=5.
Fig. 1:
The Voronoi diagrams of the
colloidal particle configurations on a square pinning array.
Filled dots: particle locations; open circles: pinning site locations.
Polygon colors indicate the coordination number of the particle at the
center of the polygon: 4 (dark blue), 5 (light blue), 6 (grey), or 7 (red).
(a) At f=4, each pinning site captures one particle and
a hexagonal lattice forms.
(b) At f = 4.5, the particles form a superlattice
structure with a periodicity of twice the pinning lattice unit cell.
(c) At f = 5.0, a square lattice forms.
(d) A stacked percentage chart of
the fraction of particles with coordination number of 4 (dark blue), 5
(light blue), 6 (grey), and 7 (red) vs filling factor f showing how
the system evolves from a hexagonal structure at f=4 to a square
structure at f=5.
|