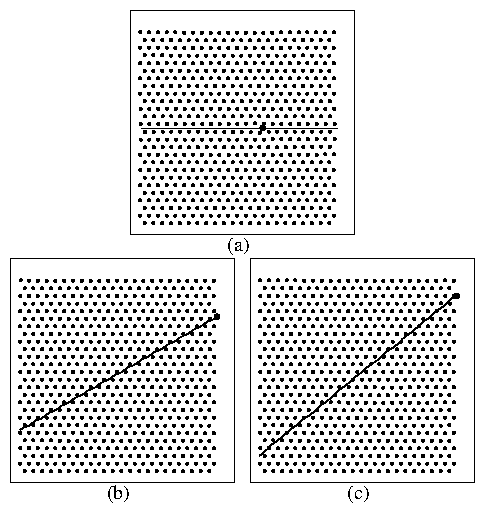
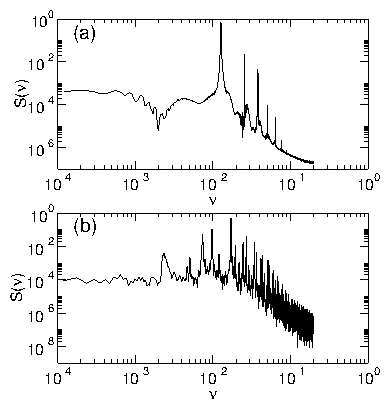
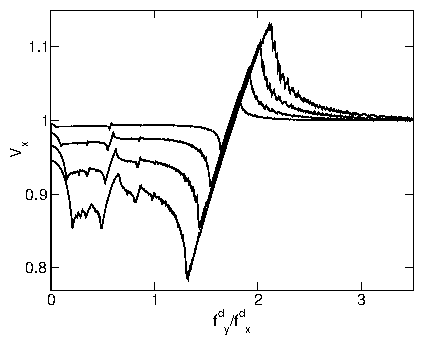
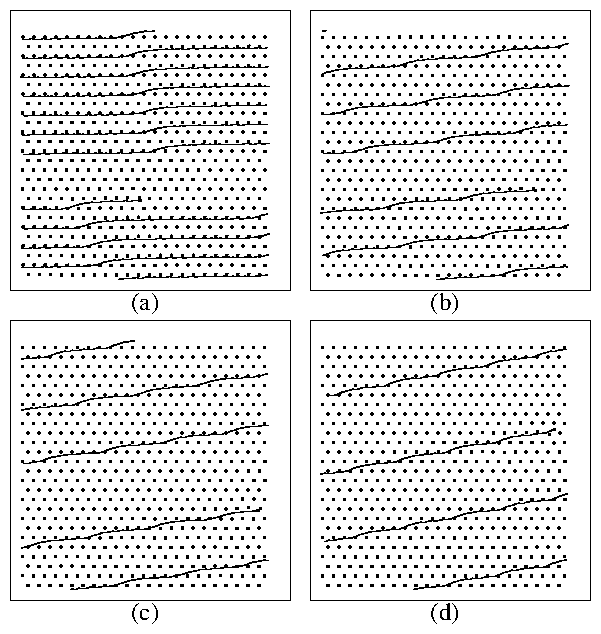
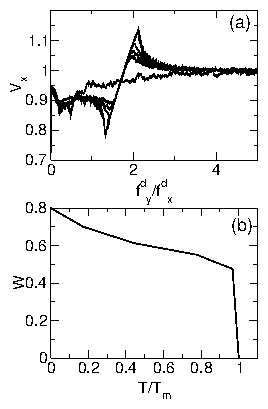
 Figure 17:
(a) Vx vs fdy/fdx for varied
T/Tm = 0.0, 0.44, 0.7, 0.9, and 1.01. Tm is the
temperature at which the non-driven lattice melts.
The curve with the largest (1,0) locking phase
(centered at fdy/fdx = 1.7) is T = 0.0.
The width of the (1,0) locking phase decreases for increasing T.
(b) Width W of the (1,0) locking vs T/Tm
for the system in Fig. 17(a).
Figure 17:
(a) Vx vs fdy/fdx for varied
T/Tm = 0.0, 0.44, 0.7, 0.9, and 1.01. Tm is the
temperature at which the non-driven lattice melts.
The curve with the largest (1,0) locking phase
(centered at fdy/fdx = 1.7) is T = 0.0.
The width of the (1,0) locking phase decreases for increasing T.
(b) Width W of the (1,0) locking vs T/Tm
for the system in Fig. 17(a).
|