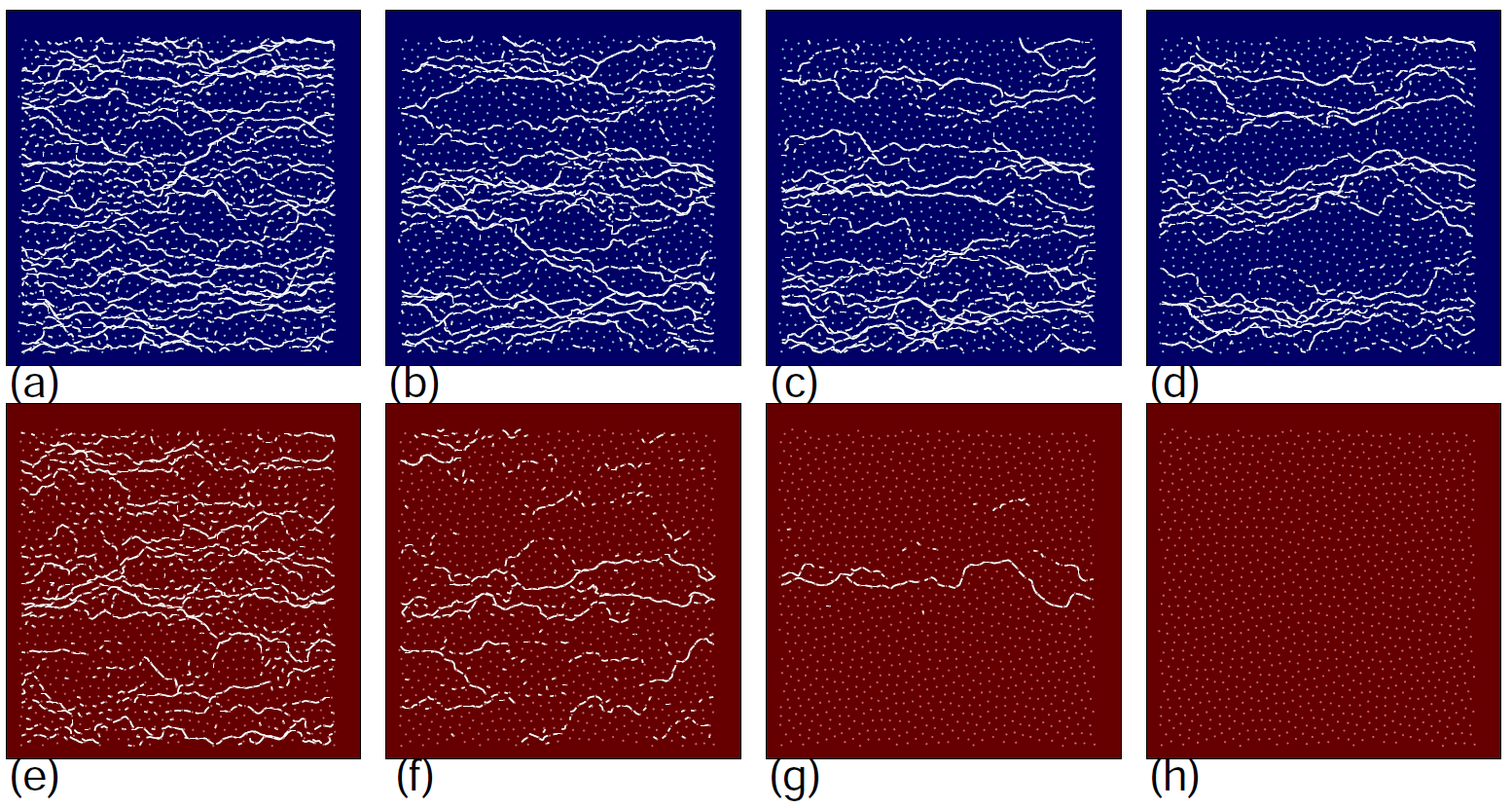
Reversible/Irreversible Transitions
Recent experimental work identified a reversible
to irreversible transition in sheared colloidal systems [D.J. Pine et al.,
Nature 438, 998 (2005)]. This is an example of a nonequilibrium
phase transition from a fluctuating state to an absorbed state in which
the fluctuations vanish and the system becomes trapped.
We demonstrate that the results from the
colloidal system can be generalized to a much wider class of systems of
driven particle systems with quenched disorder undergoing plastic flow.
In these systems, the transient times to reach steady state behavior
show a power law divergence consistent with a nonequilibrium phase transition.
We provide evidence that the transition falls into the class of directed
percolation, and make clear predictions for the behavior of the velocity noise
under cycling that can be used to identify the reversible-irreversible
transition in a system which cannot be imaged directly.
We also propose that plastic
depinning is a true phase transition which falls into the class of absorbing
phase transitions, and possibly into the class of directed or conserved
directed percolation.
Preprints:
-
Reversible to irreversible transitions for ac driven skyrmions on periodic substrates
J.C. Bellizotti Souza, N.P. Vizarim, C.J.O. Reichhardt, C. Reichhardt, and P.A. Venegas
Using atomistic simulations, we investigate the dynamical behavior of magnetic skyrmions in dimer and trimer molecular crystal arrangements, as well as bipartite lattices at 3/2 and 5/2 fillings, under ac driving over a square array of anisotropy defects. For low ac amplitudes, at all fillings we find reversible motion where the skyrmions return to their original positions at the end of each ac drive cycle and the diffusion is zero. We also identify two distinct irreversible regimes. The first is a translating regime in which the skyrmions form channels of flow in opposing directions and translate by one substrate lattice constant per ac drive cycle. The translating state appears in the dimer and trimer states, and produces pronounced peaks in the diffusivity in the direction perpendicular to the external drive. For larger ac amplitudes, we find chaotic irreversible motion in which the skyrmions can randomly exchange places with each other over time, producing long-time diffusive behavior both parallel and perpendicular to the ac driving direction.
arXiv
Papers:
-
Reversible, irreversible and mixed regimes for periodically driven disks in random obstacle arrays
D. Minogue, M.R. Eskildsen, C. Reichhardt, and C.J.O. Reichhardt
Phys. Rev. E 109, 044905 (2024).
arXiv
-
Reversible to irreversible transitions in periodic driven many-body systems and future directions for classical and quantum systems
C. Reichhardt, I. Regev, K. Dahmen, S. Okuma, and C.J.O. Reichhardt
Phys. Rev. Res. 5, 021001 (2023).
arXiv
-
Kibble-Zurek mechanism for nonequilibrium phase transitions in driven
systems with quenched disorder
C.J.O. Reichhardt, A. del Campo, and C. Reichhardt
Commun. Phys. 5, 173 (2022).
arXiv
-
Noise spectra in the reversible-irreversible transition in amorphous solids under oscillatory driving
I. Regev, C. Reichhardt, and C.J.O. Reichhardt
Model. Sim. Mater. Sci. Eng. 27, 084004 (2019). arXiv
-
Reversibility, pattern formation and edge transport in active chiral and passive disk mixtures
C. Reichhardt and C.J.O. Reichhardt
J. Chem. Phys. 150, 064905 (2019). arXiv
-
Reversible to irreversible transitions in periodically driven skyrmion systems
B.L. Brown, C. Reichhardt, and C.J.O. Reichhardt
New J. Phys. 21, 013001 (2019). arXiv
-
Crossover from clogging to jamming behaviors in heterogeneous environments
H. Peter, A. Libal, C. Reichhardt, and C.J.O. Reichhardt
Sci. Rep. 8, 10252 (2018). arXiv
-
Absorbing phase transitions and dynamic freezing in running active matter
systems
C. Reichhardt and C.J. Olson Reichhardt
Soft Matter 10, 7502 (2014). arXiv
-
Random organization in periodically driven gliding dislocations
C. Zhou, C.J. Olson Reichhardt, C. Reichhardt, and I. Beyerlein
Phys. Lett. A 378, 1675 (2014). arXiv
-
Random organization and plastic depinning
C. Reichhardt and C.J. Olson Reichhardt
Phys. Rev. Lett. 103, 168301 (2009). arXiv
-
Reversible to irreversible flow transition in periodically driven
vortices
N. Mangan, C. Reichhardt, and C.J. Olson Reichhardt
Phys. Rev. Lett. 100, 187002 (2008). arXiv
Last modified Jan 7, 2019
