New Journal of Physics 21, 013001 (2019)

Reversible to Irreversible Transitions in Periodically Driven Skyrmion Systems

B. L. Brown^1,2,3, C. Reichhardt¹, and C. J. O. Reichhardt^1,4

¹Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, United States of America
²Department of Physics, Virginia Tech, Blacksburg, Virginia 24061-0435, United States of America
³Center for Soft Matter and Biological Physics, Virgina Tech, Blacksburg, Virginia 24061-0435, United States of America
⁴Author to whom any correspondence should be addressed.

E-mail: cjrx@lanl.gov
Keywords: skyrmion, nonequilibrium phase transition, superconducting vortex
Received 15 October 2018
Revised 20 November 2018
Accepted for publication 17 December 2018
Published 8 January 2019

Abstract

We examine skyrmions driven periodically over random quenched disorder and show that there is a transition from reversible motion to a state in which the skyrmion trajectories are chaotic or irreversible. We find that the characteristic time required for the system to organize into a steady reversible or irreversible state exhibits a power law divergence near a critical ac drive period, with the same exponent as that observed for reversible to irreversible transitions in periodically sheared colloidal systems, suggesting that the transition can be described as an absorbing phase transition in the directed percolation universality class. We compare our results to the behavior of an overdamped system and show that the Magnus term enhances the irreversible behavior by increasing the number of dynamically accessible orbits. We discuss the implications of this work for skyrmion applications involving the long time repeatable dynamics of dense skyrmion arrays.

Simulation
Results
Summary
References

A great variety of many body systems exhibit nonequilibrium phases under an applied drive [1], including assemblies of colloidal particles [2,3], vortices in type-II superconductors [4,5], sliding friction [6], active matter [7], dislocation motion [8], and geological systems [9]. Despite the ubiquity of these systems, it is often experimentally difficult to find a protocol that will produce distinct nonequilibrium phases separated by clear transitions, and in many cases it is not even clear what order parameter or measures should be used.

In 2005 Pine et al. [10] examined a fairly simple system of a dilute assembly of colloidal particles in an overdamped medium subjected to periodic shearing. They introduced a new stroboscopic measure in which the positions of the particles at the end of each shear cycle are compared to the positions at the end of the previous cycle. Pine et al. found that as a function of the distance over which the particles are sheared, there is a transition from a reversible state, in which all particles return to the same positions after each cycle, to an irreversible state, in which the particles do not return to the same positions and exhibit chaotic dynamics with a long time diffusive behavior. The threshold shearing distance decreases as the density of particles increases due to an increase in the frequency of particle-particle collisions. In further work on this system, Corte et al. [11] found that the initial motion is always irreversible but that over time the particles organize into a steady state that is either reversible or irreversible depending on the shearing distance. The number of shearing cycles required to reach a steady state diverges as a power law at a critical point, suggesting that the reversible-irreversible transition is an example of a nonequilibrium phase transition. The power law exponents are consistent with those expected for an absorbing phase transition in the directed percolation universality class [11,12,13]. In the reversible regime, all the fluctuations are lost and the system is absorbed into a state which it cannot escape. More recent work has shown that the periodically sheared colloidal system organizes into a reversible state in which particle-particle collisions no longer occur and large-scale density fluctuations in the particle positions are suppressed, giving hyperuniform order rather than a truly random state [14,15,16,17]. Similar reversible to irreversible transitions have been observed in a wide range of other periodically driven systems that are much more strongly interacting than the colloidal particles, such as granular matter [18,19,20,21], dislocations [22,23], amorphous solids [24,25,26,27], polycrystalline solids [28], charged colloids [29], and vortices in type-II superconductors [30,31,32]. The dynamics of most of these systems is overdamped, and little is known about how nondissipative dynamics would affect a reversible to irreversible transition.

An important example of nondissipative interacting particles is skyrmions in chiral magnets. Discovered in 2009, magnetic skyrmions are nanometer-sized spin textures that have many similarities to vortices in type-II superconductors, in that they form a triangular lattice in the absence of quenched disorder [33,34,35] and undergo driven motion when subjected to an applied current [33,36,37,38,39,40,41,42,43]. A key difference between skyrmions and the systems described above is that the skyrmion dynamics includes a pronounced nondissipative Magnus term [33,36,38]. The Magnus term generates velocity components that are perpendicular to the net force experienced by the skyrmion, unlike the damping term which aligns the skyrmion velocity with the external forces. In the absence of quenched disorder, under an applied drive the skyrmions move at an angle to the driving direction called the intrinsic skyrmion Hall angle θ_sk^int=tan⁻¹(α_m/α_d), given by the ratio of the Magnus term α_m to the dissipative term α_d [33]. When the Magnus term is zero, θ_sk^int = 0^°. The observed skyrmion Hall angle θ_sk has been shown to become drive dependent in the presence of pinning due to a side jump of the skyrmions produced by the Magnus term as the skyrmions move through the pinning sites, which decreases in magnitude as the skyrmion velocity increases, giving a saturation to θ_sk=θ_sk^int at high drives [44,45,46,47]. Continuum-based simulations of skyrmions confirm that the drive dependence of the skyrmion Hall angle exists when disorder is present and is absent in the disorder-free limit [42,48]. In skyrmion experiments, after the skyrmions depin they enter a flowing phase in which θ_sk is directly observed to increase with drive before saturating at high drives [49,50]. A similar increase in θ_sk as a function of ac drive has also been found experimentally [51].

Skyrmions can potentially be used for a variety of applications similar to those proposed for magnetic domain walls, where the smaller size and higher mobility of the skyrmions give them numerous advantages over domain wall systems [52]. Many of the applications require the motion of the skyrmions to be reversible, and experiments involving ac drives have shown that the dynamics of isolated skyrmions can remain reversible over a large number of drive cycles [51]. For applications in which it is necessary for dense arrays of interacting skyrmions to maintain reversible motion over many cycles, it is important to develop an understanding of the onset of periodic reversible behaviors and to characterize the irreversible behaviors as a function of the net displacements of the skyrmions under an ac drive.

In this work we employ a periodic driving protocol to a particle-based model of a skyrmion assembly interacting with random disorder. We characterize the system by analyzing the net displacement of the skyrmions between the beginning and end of each drive cycle, where a fully reversible state corresponds to a net displacement of zero. By varying the driving period, which changes the distance d that an isolated skyrmion in the absence of disorder can travel during a single drive cycle, we find that there is a well defined critical value d_c below which the system reaches a steady reversible state and above which a steady irreversible state emerges. Near d_c we find a characteristic time scale τ for the system to reach a steady state, where τ ∝ |d − d_c|^−ν with exponent ν ≈ 1.3. The divergence of τ at the reversible-irreversible transition is similar to what is observed in the periodic shearing of dilute colloids [11] and jammed solids [25,27] as a function of increasing d, and the power law exponent is also similar, suggesting that d_c is a critical point separating an absorbing reversible state from a fluctuating irreversible state in the directed percolation universality class [12]. In the overdamped limit, which represents strongly damped skyrmions as well as vortices in type-II superconductors, we observe a similar power law time scale divergence in the reversible regime, but we find evidence that there are two distinct transitions in the irreversible regime. In the first transition, the motion of the particles becomes irreversible in the direction parallel to the drive when a dynamically reordered smectic state appears, and in the second transition, the motion becomes irreversible both parallel and perpendicular to the drive.

Simulation

We simulate N=245 particles in a two-dimensional (2D) sample of size [2/(√3)]L×L with periodic boundary conditions in the x and y directions. We use a modified Thiele equation for the particle-particle interactions as in previous works [44,46,47,53,54], with F^ss_i=∑^N_{i ≠ j}F^ss₀K₁(R_ij)∧R_ij, where F₀^ss=1, K₁ is a modified Bessel function, R_ij=|R_i−R_j| is the distance between particles i and j, and ∧R_ij=(R_i−R_j)/R_ij. We take interactions between particles i and j with R_ij > 7 to be negligible. In this work we choose L=64 which sets the lattice constant a₀ ≈ 4.56 in the clean system, placing us in the strongly interacting regime. We model the quenched disorder as N_p=113 randomly placed nonoverlapping attractive harmonic pinning sites with radius r_p=0.3 such that F^p_i=∑^N_p_k F^p₀(R_ki/r_p)Θ(r_p−R_ki)∧R_ki where F^p₀=1.5, Θ is the Heaviside step function, R_ki=|R_k^p−R_i| is the distance between the pinning site k and particle i, and ∧R_ki=(R_k^p−R_i)/R_ki. The strong repulsive particle-particle interactions prevent more than one particle from occupying the same pinning site. The particles are driven by a periodic current applied to the sample which we model as a square wave with period T: F^AC=F^AC₀sgn(sin(2πt/T))∧x, where F^AC₀=1.3.

The Langevin equations of motion are as follows:

α_dv_i + α_m

×v_i = F_i^ss + F_i^p + F^AC,

(1)

where v_i is the velocity of particle i, α_d is the damping coefficient, and α_m determines the strength of the Magnus term. We use a standard fourth-order Runge-Kutta method to integrate Eq. (1) with a time step of ∆t=0.05. In skyrmion systems, the nondissipative Magnus term is important to the dynamics, but for other systems such as vortices in type-II superconductors, the Magnus force is negligible and the dynamics are described by Eq. (1) in the overdamped limit α_m→ 0 [55]. In this work we focus on two cases: the skyrmion limit with α_m/α_d=1 and the overdamped limit with α_m/α_d=0. In order to facilitate comparisons of the skyrmion and overdamped limits we fix α_m² +α_d²=1. We report the magnitude of the ac drive in terms of the displacement d of an isolated particle in the absence of disorder during half of a drive cycle, d=[(F^AC₀T)/2]. The particles are initialized in a triangular lattice and are allowed to relax under the influence of the quenched disorder. Once the relaxation is complete, we apply the periodic driving force and measure the mean square displacement, R²_α(n), in the x and y directions as follows:

R²_α(n) =

N
∑
i

[(

(nT)−R_i(0)) ·

]²

(2)

where α = (x,y), n is the number of drive cycles over which the displacement is measured, ~R_i is the absolute position of particle i without reflection back into the periodic box, and the brackets indicate an average over different quenched disorder realizations. After a transient time, the system reaches a steady state characterized by either reversible or irreversible flow depending on the drive period. The particle trajectories in the irreversible regime are chaotic and R²_α behaves as an anisotropic random walk, while in the reversible regime R²_α approaches a constant value. We also measure the fraction of active particles, F_a(n), as a function of the number of cycles. A particle is defined to be `active' if it does not return to a circular region of radius r_a=2r_p centered on its position at the end of the last drive cycle, giving

F_a(n)=

N
∑
i

Θ(|

(nT)−

((n−1)T)|−r_a)

(3)

In reversible flow, there are no active particles and F_a → 0, while F_a approaches a finite value when the flow is irreversible.

Results

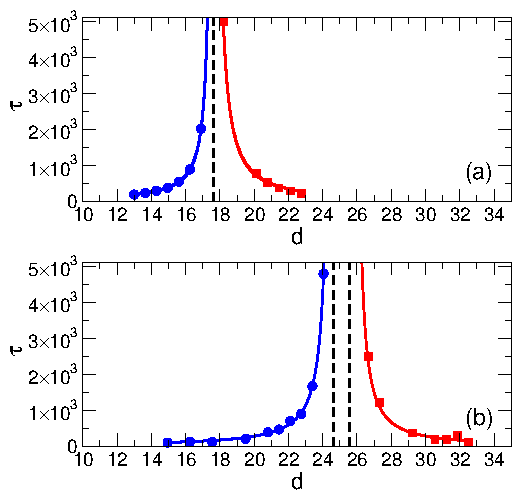
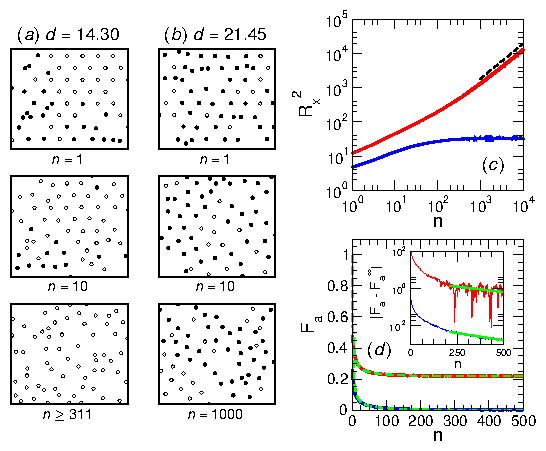
Figure 1: (a,b) Images of particle positions in a portion of the sample in the skyrmion limit with α_m/α_d=1. Filled circles are `active' particles that do not return to the same position after each drive cycle, and open circles are inactive particles that move reversibly. (a) A reversible state at d=14.30 after n=1, 10, and 311 cycles, from top to bottom. (b) An irreversible state at d=21.45 after n=1, 10, and 1000 cycles, from top to bottom. (c) The mean square particle displacement in the x direction, R_x², vs cycle number n for d=14.30 (blue) and d=21.45 (red). The dashed line is a fit to R_x² ∝ n. (d) The fraction F_a of active particles vs n for d=14.30 (blue) and d=21.45 (red). The dashed lines are fits to Eq. (4). The standard error of F_a is on the order of 10⁻³. The inset shows |F_a−F_a^∞| for the same values of d as in the main plot, but the d=21.45 (red) curve has been translated vertically to avoid overlap. At long times, F_a exponentially decays with n. The solid green lines are guides to the eye.

Under small displacements, the particle trajectories become reversible after a transient time interval of reorganization, and the system returns to the same configuration at the end of each drive cycle. Figure 1(a,b) shows snapshots of a portion of the system in the skyrmion limit for reversible and irreversible flows. For the reversible case with d=14.30 in Fig. 1(a), the system reaches an absorbed completely reversible state after n=311 cycles of the drive. As d increases, we find a transition to irreversible flow, illustrated for d=21.45 in Fig. 1(b), in which the motion of the particles becomes chaotic and each active particle moves further away from its initial location after each cycle. Here the fraction F_a of active particles remains finite since the system is unable to find a reversible configuration. In Fig. 1(c) we plot the mean square displacement parallel to the drive, R²_x, versus n for the reversible and irreversible states. At d=14.30 when the motion is reversible, R²_x approaches a constant value, while for d=21.45 when the system is irreversible, R²_x increases linearly with time at long times, consistent with a one-dimensional random walk. This result is in agreement with Ref. [30], where similar behavior is observed for superconducting vortices in the irreversible flow regime. In Fig. 1(d), we plot F_a versus n, which goes to zero when d=14.30 in the reversible state, and saturates to a finite value for d=21.45 in the irreversible state. Following Corté et al. [11], we find that the active fraction is well fit by the following relaxation function:

F_a=(F_a⁰ − F_a^∞)e^−t/τt^−α + F_a^∞ ,

(4)

where F_a⁰ and F_a^∞ are the initial and steady state values of F_a, respectively, and τ is the characteristic time at which the relaxation crosses over from a power-law behavior with exponent α, described further in Fig. 4, to an exponential decay. The dashed lines in Fig. 1(d) indicate fits of F_a to Eq. (4).

Figure 2: Contour plots of the average motion of an individual particle around its mean position in the steady state for cycles n=1000 to n=2000 plotted as a function of y vs x in units of the drive displacement d. The contours indicate areas in which each point has a minimum of 0.03% (dark blue), 0.3% (medium blue), 0.75% (light blue), and 1.5% (orange) likelihood of being visited by the particle. The dashed lines, which are aligned with the drive in the overdamped limit and are at an angle θ ≈ 41^° with respect to the drive in the skyrmion limit, indicate the average motion δm_p along the first principal axis obtained via a principal component analysis. (a) Reversible motion in the skyrmion limit with α_m/α_d=1 and d=14.3, where δm_p=1.2d. (b) Irreversible motion in the skyrmion limit with α_m/α_d=1 and d=29.9, where δm_p=8.8d. (c) Reversible motion in the overdamped limit with α_m/α_d=0 and d=14.3, where δm_p=0.87d. (d) Irreversible motion in the overdamped limit with α_m/α_d=0 and d=29.9, where δm_p=3.0d.

To understand the steady state behavior of the particles during each cycle, we construct a contour plot of the average motion of an individual particle around its mean position in the steady state. For cycles n=1000 through n=2000, well outside the regime of transient behavior, we sample the position of each particle relative to its mean location every 0.1T time steps, and find the probability that the particle will be observed at a given relative location, as plotted in Fig. 2. The dashed line at the center of each panel of Fig. 2 indicates the average motion δm_p along the first principal axis obtained via principal component analysis. For skyrmions with α_m/α_d=1, shown in Fig. 2(a,b) for d=14.30 and d=29.9, respectively, the principal axis is at an angle of θ ≈ 41^° with respect to the drive direction. This is very close to the intrinsic skyrmion Hall angle θ_sk^int = 45^°, as expected based on both simulations and experiments that have previously demonstrated a saturation of the skyrmion Hall angle to the disorder free value at large drives [44,46,48,49,50,51]. For the reversible state illustrated in Fig. 2(a), the particles move with the drive but return to their starting positions after each cycle, and therefore we expect the motion to be limited by the drive displacement, d. This is indeed the case, as indicated by the fact that δm_p ≈ 1.2d. In contrast, in the irreversible state shown in Fig. 2(b), the particles undergo an anisotropic random walk biased along the first principal axis and do not return to their starting locations. The average motion, δm_p ≈ 8.8d, is much larger than in the reversible limit. For overdamped particles with α_m/α_d=0, the contour plots of the average motion in Fig. 2(c,d) for the reversible state at d=14.3 and the irreversible state at d=29.9 indicate that the overall motion is reduced compared to the skyrmion limit, with δm_p=0.87d in the reversible state and δm_p=3.0d in the irreversible state.

Figure 3: Characteristic time τ to reach steady state vs drive displacement d for the skyrmion system with α_m/α_d=1. A transition from reversible flow (blue circles) to irreversible flow (red squares) occurs at the critical displacement d_c ≈ 17.6 (dashed line). The blue and red curves indicate power law fits to τ ∝ |d−d_c|^−ν with ν ≈ 1.26 in the reversible state and ν ≈ 1.30 in the irreversible state. Inset: The same data plotted as τ vs |d−d_c| on a log-log scale.

For the skyrmion system with α_m/α_d=1, we obtain the characteristic time scale τ for a series of drive displacements d by fitting F_a to Eq. (4). In Fig. 3 we plot τ versus d for both the reversible and irreversible regimes, and find a divergence of τ at a critical displacement d_c ≈ 17.6, consistent with a dynamical phase transition. On both sides of the transition, τ has the power law form τ ∼ |d−d_c|^−ν, as shown in the inset of Fig. 3, with ν ≈ 1.26 in the reversible regime and ν ≈ 1.30 in the irreversible regime. These exponents are similar to the value ν ≈ 1.295 expected for 2D directed percolation [12] as well as to the value ν ≈ 1.33 observed in the sheared colloid simulations of Ref. [11].

Figure 4: F_a, the fraction of active particles, vs n for the skyrmion limit with α_m/α_d=1 for d/d_c=1.07, 1.03, 1.001, and 0.960, from top to bottom. The dashed lines are power law fits to F_a ∝ n^−α with α = 0.38 (magenta) and α = 0.49 (orange).

In Fig. 4 we plot the active fraction F_a as a function of drive cycle n in the skyrmion system with α_m/α_d=1 near the transition for drive displacements d/d_c=0.960 to 1.07. At long times and near the critical displacement, we find a power law behavior with F_a ∝ n^−α, where α = 0.49 at d/d_c=1.001. This is similar to the expected exponents α ≈ 0.451 for 2D directed percolation and α = 0.5 for 2D conserved directed percolation [22].

Figure 5: τ vs d in the reversible (blue circles) and irreversible (red squares) regimes, along with the critical value d=d_c (dashed lines) and power law fits to τ ∝ |d−d_c|^−ν (solid lines). (a) The skyrmion system with α_m/α_d=1, already shown in Fig. 3, has d_c=17.6. (b) The overdamped system with α_m/α_d=0 has d_c=24.6 with ν = 1.33 in the reversible regime, and d_c=25.8 with ν = 1.31 in the irreversible regime.

In Fig. 5(a), we replot the values of τ versus d for the skyrmion system from Fig. 3 in order to compare them with the behavior of τ in the overdamped system, shown in Fig. 5(b). We find power law exponents of ν = 1.33 in the reversible state and ν = 1.31 in the irreversible state for the overdamped system, similar to what we observe for the skyrmion system, indicating that omission of the Magnus term does not appear to change the universality class of the transition. There is, however, a large change in the value of the critical displacement d_c, which falls at d_c ≈ 17.6 in the skyrmion system but shifts to the much higher value d_c ≈ 25 in the overdamped system. The Magnus term was previously shown to enhance the effect of an external noise [54], and the suppression of the reversible regime that we observe when we include the Magnus term suggests that the Magnus term also enhances the chaotic nature of the motion of skyrmions over the quenched disorder, making it more difficult for the system to reach a reversible configuration.

Figure 6: The characteristic time τ_⊥ obtained from R²_⊥, the cycle-to-cycle displacement transverse to the drive, vs d for the overdamped system with α_m/α_d=0, along with solid lines showing fits to τ_⊥ ∝ |d−d_c^⊥|^−ν. The dashed lines indicate the two values of d_c=24.6 and d_c=25.8 found in Fig. 5(b) from fitting τ on either side of the transition. Here we find d_c^⊥=25.8 on both sides of the transition.

For the overdamped system in Fig. 5(b), we find that the value of d_c is slightly different depending on whether the transition is approached from the reversible or the irreversible side. In the reversible regime, d_c ≈ 24.6, but in the irreversible regime, d_c ≈ 25.8. This gap could indicate that there are two transitions instead of only one. The first transition is from fully reversible flow to a smectic state in which the flow is reversible transverse to the drive but irreversible in the direction of the drive. The second transition is from this smectic state to fully irreversible flow. To test this idea, we measure the cycle-to-cycle displacement in the transverse direction, R²_⊥(n)=〈(1/N)∑_i^N[(~R_i(nT)−~R_i((n−1)T))·∧y]²〉, and obtain a characteristic time τ_⊥ by fitting R²_⊥ to Eq. (4). We plot τ_⊥ versus d on both sides of the transition in Fig. 6, where the dashed lines indicate the two values of d_c obtained by fitting the data in Fig. 5. By fitting τ_⊥ ∝ |d−d_c^⊥|^−ν, we find that d_c^⊥=25.8 in both the reversible and irreversible regimes, indicating that there is a single transition for motion perpendicular to the drive at d_c^⊥=25.8. The transition for motion parallel to the drive must then occur at the lower value of d_c^||=24.6. For 24.6 < d < 25.8, the flow is expected to follow channels aligned with the driving direction. This flow should be smectic in nature, so that the particles can slide past one another irreversibly in the direction of the drive while remaining reversibly locked to a single channel with no motion in the direction transverse to the drive. It would be necessary to simulate much larger systems to clearly resolve the behavior of the individual channels. If the drive is applied along the y direction, the two transitions are interchanged. It would be interesting to slowly vary the drive displacement across the two transitions to see whether hysteresis occurs in the fraction of active particles. It may also be possible to control the size of the gap between the two transitions by applying a second ac drive at an angle to the original drive. Another potential avenue for future research is in the area of Floquet engineering [56]. In particular, it may be possible to use the Floquet-Magnus expansion to obtain an approximate description of the relaxation to steady state, as recently demonstrated for the Kapitza pendulum with friction [57].

Summary

We show that both skyrmions and overdamped particles that are periodically driven over quenched disorder undergo a transition as a function of drive period from a reversible state at small drive periods, in which the particles return to the same position after each drive cycle, to an irreversible state at large drive periods, in which the particle positions gradually diffuse from cycle to cycle. Near the transition, the fraction of active particles has a power law time dependence with an exponent α ≈ 1/2 in the skyrmion limit, consistent with an absorbing phase transition. The characteristic time required to reach a steady state diverges as a power law at the transition with an exponent similar to that expected for directed percolation for both the skyrmions and overdamped particles, suggesting that inclusion of a Magnus term in the particle dynamics does not change the universality class of the transition. The Magnus term enhances the random motion generated by the quenched disorder, and as a result the range of reversible behavior is much smaller for the skyrmion system than for the overdamped particles. We find evidence that the overdamped system first transitions from the reversible regime to a smectic state, and then undergoes a second transition from smectic flow to fully irreversible flow as the drive period is increased.

Acknowledgments

We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD program for this work. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396 and through the LANL/LDRD program.

ORCID iDs

C J O Reichhardt https://orcid.org/0000-0002-3487-5089

References

[1]: C. Reichhardt and C. J. Olson Reichhardt, Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review, Rep. Prog. Phys. 80, 026501 (2017).
[2]: A. Pertsinidis and X. S. Ling, Statics and Dynamics of 2D Colloidal Crystals in a Random Pinning Potential, Phys. Rev. Lett. 100, 028303 (2008).
[3]: P. Tierno, Depinning and Collective Dynamics of Magnetically Driven Colloidal Monolayers, Phys. Rev. Lett. 109, 198304 (2012).
[4]: S. Bhattacharya and M. J. Higgins, Dynamics of a Disordered Flux Line Lattice, Phys. Rev. Lett. 70, 2617 (1993).
[5]: G. Shaw, P. Mandal, S. S. Banerjee, A. Niazi, A. K. Rastogi, A. K. Sood, S. Ramakrishnan, and A. K. Grover, Critical behavior at depinning of driven disordered vortex matter in 2H-NbS₂, Phys. Rev. B 85, 174517 (2012).
[6]: A. Vanossi, N. Manini, M. Urbakh, S. Zapperi, and E. Tosatti, Modeling friction: From nanoscale to mesoscale, Rev. Mod. Phys. 85, 529 (2013).
[7]: C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, Active Brownian particles in complex and crowded environments, Rev. Mod. Phys. 88, 045006 (2016).
[8]: M.-C. Miguel, A. Vespignani, S. Zapperi, J. Weiss, and J.-R. Grasso, Intermittent dislocation flow in viscoplastic deformation, Nature (London) 410, 667 (2001).
[9]: J. M. Carlson and J. S. Langer, Properties of earthquakes generated by fault dynamics, Phys. Rev. Lett. 62, 2632 (1989).
[10]: D. J. Pine, J. P. Gollub, J. F. Brady, and A. M. Leshansky, Chaos and threshold for irreversibility in sheared suspensions. Nature 438, 997 (2005).
[11]: L. Corte, P. M. Chaikin, J. P. Gollub, and D. J. Pine, Random organization in periodically driven systems, Nat. Phys. 4, 420 (2008).
[12]: H. Hinrichsen, Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815 (2000).
[13]: G. I. Menon and S. Ramaswamy, Universality class of the reversible-irreversible transition in sheared suspensions, Phys. Rev. E 79, 061108 (2009).
[14]: D. Hexner and D. Levine, Hyperuniformity of Critical Absorbing States, Phys. Rev. Lett. 114, 110602 (2015).
[15]: J. H. Weijs, R. Jeanneret, R. Dreyfus, and D. Bartolo, Emergent Hyperuniformity in Periodically Driven Emulsions, Phys. Rev. Lett. 115, 108301 (2015).
[16]: E. Tjhung and L. Berthier, Hyperuniform Density Fluctuations and Diverging Dynamic Correlations in Periodically Driven Colloidal Suspensions, Phys. Rev. Lett. 114, 148301 (2015).
[17]: J. Wang, J. M. Schwarz and J. D. Paulsen, Hyperuniformity with no fine tuning in sheared sedimenting suspensions, Nat. Commun. 9, 2836 (2018).
[18]: J. R. Royer and P. M. Chaikin, Precisely cyclic sand: Self-organization of periodically sheared frictional grains, Proc. Natl. Acad. Sci. (USA) 112, 49 (2015).
[19]: C. F. Schreck, R. S. Hoy, M. D. Shattuck, and C. S. O’Hern, Particle-scale reversibility in athermal particulate media below jamming, Phys. Rev. E 88, 052205 (2013).
[20]: L. Milz and M. Schmiedeberg, Connecting the random organization transition and jamming within a unifying model system, Phys. Rev. E 88, 062308 (2013).
[21]: M. O. Lavrentovich, A. J. Liu, and S. R. Nagel, Period proliferation in periodic states in cyclically sheared jammed solids, Phys. Rev. E 96, 020101 (2017).
[22]: C. Zhou, C.J. Olson Reichhardt, C. Reichhardt, and I. Beyerlein, Random organization in periodically driven gliding dislocations, Phys. Lett. A 378, 1675 (2014).
[23]: X. Ni, H. Zhang, D. B. Liarte, L. W. McFaul, K. A. Dahmen, J. P. Sethna, and J. R. Greer, Yield precursor dislocation avalanches in small crystals: the irreversibility transition, arXiv:1802.04040 (unpublished).
[24]: I. Regev, T. Lookman, and C. Reichhardt, Onset of irreversibility and chaos in amorphous solids under periodic shear, Phys. Rev. E 88, 062401 (2013).
[25]: I. Regev, J. Weber, C. Reichhardt, K. A. Dahmen, and T. Lookman, Reversibility and criticality in amorphous solids, Nat. Commun. 6, 8805 (2015).
[26]: N. V. Priezjev, Reversible plastic events during oscillatory deformation of amorphous solids, Phys. Rev. E 93, 013001 (2016).
[27]: P. Leishangthem, A. D. S. Parmar, and S. Sastry, The yielding transition in amorphous solids under oscillatory shear deformation, Nat. Commun. 8, 14653 (2017).
[28]: P. K. Jana, M. J. Alava, and S. Zapperi, Irreversibility transition of colloidal polycrystals under cyclic deformation, Sci. Rep. 7, 45550 (2017).
[29]: C. Reichhardt and C. J. Olson Reichhardt, Random Organization and Plastic Depinning, Phys. Rev. Lett. 103, 168301 (2009).
[30]: N. Mangan, C. Reichhardt, and C. J. Olson Reichhardt, Reversible to Irreversible Flow Transition in Periodically Driven Vortices, Phys. Rev. Lett. 100, 187002 (2008).
[31]: S. Okuma, Y. Tsugawa, and A. Motohashi, Transition from reversible to irreversible flow: Absorbing and depinning transitions in a sheared-vortex system, Phys. Rev. B 83, 012503 (2011).
[32]: M. Dobroka, Y. Kawamura, K. Ienaga, S. Kaneko, and S. Okuma, Memory formation and evolution of the vortex configuration associated with random organization, New J. Phys. 19, 053023 (2017).
[33]: N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol. 8, 899 (2013).
[34]: S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Skyrmion lattice in a chiral magnet, Science 323, 915 (2009).
[35]: X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Real-space observation of a two-dimensional skyrmion crystal, Nature (London) 465, 901 (2010).
[36]: T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, and A. Rosch, Emergent electrodynamics of skyrmions in a chiral magnet, Nat. Phys. 8, 301 (2012).
[37]: X.Z. Yu, N. Kanazawa, W.Z. Zhang, T. Nagai, T. Hara, K. Kimoto, Y. Matsui, Y. Onose, and Y. Tokura, Skyrmion flow near room temperature in an ultralow current density, Nat. Commun. 3, 988 (2012).
[38]: J. Iwasaki, M. Mochizuki, and N. Nagaosa, Universal current-velocity relation of skyrmion motion in chiral magnets, Nat. Commun. 4, 1463 (2013).
[39]: W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F. Y. Fradin, J. E. Pearson, Y. Tserkovnyak, K. L. Wang, O. Heinonen, S. G. E. te Velthuis, and A. Hoffmann, Blowing magnetic skyrmion bubbles, Science 349, 283 (2015).
[40]: D. Liang, J. P. DeGrave, M. J. Stolt, Y. Tokura, and S. Jin, Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect, Nat. Commun. 6, 8217 (2015).
[41]: S. Woo, K. Litzius, B. Krüger, M.-Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R. M. Reeve, M. Weigand, P. Agrawal, I. Lemesh, M.-A. Mawass, P. Fischer, M. Kläui, and G. S. D. Beach, Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets, Nat. Mater. 15, 501 (2016).
[42]: W. Legrand, D. Maccariello, N. Reyren, K. Garcia, C. Moutafis, C. Moreau-Luchaire, S. Collin, K. Bouzehouane, V. Cros, and A. Fert, Room-Temperature Current-Induced Generation and Motion of sub-100 nm Skyrmions, Nano Lett. 17, 2703 (2017).
[43]: R. Tolley, S. A. Montoya, and E. E. Fullerton, Room-temperature observation and current control of skyrmions in Pt/Co/Os/Pt thin films, Phys. Rev. Mater. 2, 044404 (2018).
[44]: C. Reichhardt, D. Ray, and C. J. Olson Reichhardt, Collective Transport Properties of Driven Skyrmions with Random Disorder, Phys. Rev. Lett. 114, 217202 (2015).
[45]: J. Müller and A. Rosch, Capturing of a magnetic skyrmion with a hole, Phys. Rev. B 91, 054410 (2015).
[46]: C. Reichhardt and C. J. O. Reichhardt, Noise fluctuations and drive dependence of the skyrmion Hall effect in disordered systems, New J. Phys. 18, 095005 (2016).
[47]: C. Reichhardt, D. Ray, and C. J. Olson Reichhardt, Quantized transport for a skyrmion moving on a two-dimensional periodic substrate, Phys. Rev. B 91, 104426 (2015).
[48]: J.-V. Kim and M.-W. Yoo, Current-driven skyrmion dynamics in disordered films, Appl. Phys. Lett. 110, 132404 (2017).
[49]: W. Jiang, X. Zhang, G. Yu, W. Zhang, X. Wang, M. B. Jungfleisch, J. E. Pearson, X. Cheng, O. Heinonen, K. L. Wang, Y. Zhou, A. Hoffmann, and S. G. E. te Velthuis, Direct observation of the skyrmion Hall effect, Nat. Phys. 13, 162 (2017).
[50]: S. Woo, K.M. Song, X. Zhang, Y. Zhou, M. Ezawa, X. Liu, S. Finizio, J. Raabe, N.J. Lee, S.-I. Kim, S.-Y. Park, Y. Kim, J.-Y. Kim, D. Lee, O.J. Lee, J.W. Choi, B.-C. Min, H.C. Koo, and J. Chang, Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films, Nat. Commun. 9, 959 (2018).
[51]: K. Litzius, I. Lemesh, B. Krüger, P. Bassirian, L. Caretta, K. Richter, F. Büttner, K. Sato, O. A. Tretiakov, J. Förster, R. M. Reeve, M. Weigand, I. Bykova, H. Stoll, G. Schütz, G. S. D. Beach, and M. Kläui, Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy, Nat. Phys. 13, 170 (2017).
[52]: A. Fert, V. Cros, and J. Sampaio, Fert A, Cros V and Sampaio J 2013 Skyrmions on the track Nat. Nanotechnol. 8 152–6
[53]: S.-Z. Lin, C. Reichhardt, C.D. Batista, and A. Saxena, Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep, Phys. Rev. B 87, 214419 (2013).
[54]: B. L. Brown, U. C. Täuber, and M. Pleimling, Effect of the Magnus force on skyrmion relaxation dynamics, Phys. Rev. B 97, 020405 (2018).
[55]: G. Blatter, M.V. Feigel'man, V.B. Geshkenbein, A.I. Larkin, and V.M. Vinokur, Vortices in high-temperature superconductors, Rev. Mod. Phys. 66, 1125 (1994).
[56]: M. Bukov, L. D'Alessio, and A. Polkovnikov, Universal high-frequency behavior of periodically driven systems: from dynamical stabilization to Floquet engineering, Adv. Phys. 64, 139 (2015).
[57]: S. Higashikawa, H. Fujita, and M. Sato, Floquet engineering of classical systems, arXiv:1810.01103 (unpublished).

File translated from T_EX by T_THgold, version 4.00.
Back to Home