Physics Letters A 378, 1675 (2014)

Random Organization in Periodically Driven Gliding Dislocations

C. Zhou^a,b, C. J. Olson Reichhardt^b,*, C. Reichhardt^b, I. Beyerlein^b

^aDepartment of Materials Science & Engineering, Missouri University of Science and Technology, Rolla, MO 65409, USA
^bCenter for Nonlinear Studies and Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA

Received 13 September 2013
Accepted 13 March 2014
Available online 16 April 2014
Communicated by R. Wu

Abstract

We numerically examine dynamical irreversible to reversible transitions and random organization for periodically driven gliding dislocation assemblies using the stroboscopic protocol developed to identify random organization in periodically driven dilute colloidal suspensions. We find that the gliding dislocations exhibit features associated with random organization and evolve into a dynamically reversible state after a transient time extending over a number of cycles. At a critical shearing amplitude, the transient time diverges. When the dislocations enter the reversible state they organize into patterns with fragmented domain wall type features.

1 Introduction
2 Computational Details
3 Results and Discussion
3.1 Transient times
4 Conclusion
References

1 Introduction

Recent experiments and simulations on non-thermal dilute colloidal systems under periodic external driving [1,2,3,4,5] have revealed a transition from irreversible to reversible behavior in the colloidal particle positions after a number of cycles of the external drive are applied [1,3,2,6]. The different regimes are identified by marking the particle positions at the beginning of each drive cycle and comparing them to the positions at the end of the cycle [1,2]. In general the system always behaves irreversibly for the first few cycles, but either settles into a reversible state or remains irreversible. As described in Ref. [1], in the irreversible regime, the particle positions differ at the beginning and end of the cycle, and the accumulated displacements over many cycles correspond to an anisotropic random walk. In the reversible regime, the particles all return to the same positions at the end of each cycle so there is no diffusive behavior or particle mixing. For low driving amplitudes τ_ext, the system evolves into a reversible state after a transient time t_n of only a few cycles. As τ_ext increases, t_n increases and undergoes a power law divergence at a critical driving amplitude τ_c. For drives above τ_c, the system remains irreversible for an arbitrary number of cycles, but there is still a transient decay into the steady irreversible state during a time t_n, which diverges as a power law near τ_c. The dilute colloidal particles rearrange themselves in the reversible state so that they no longer interact, and since these states lack spatial organization, they were termed 'randomly organized.' The power law divergence of t_n has been interpreted[7] to indicate that the reversible to irreversible transition is a nonequilibrium phase transition.

Reversible to irreversible transitions and random organization in periodically driven systems with quenched disorder have also been studied for vortices in type-II superconductors, where behavior very similar to that of the dilute colloidal suspensions occurs: the system organizes into reversible states and has divergent transient times on either side of a critical drive amplitude [8,9,10,11]. The vortices have much longer range interactions than the colloidal particles, and in the reversible state the vortices are still strongly interacting with each other, indicating that the idea of random organization can be extended beyond systems with simple contract interactions. Random organization has also been studied in the context of plastic depinning of colloidal particles and vortices, where a divergent transient time appears at the pinned to sliding transition [12,13,14,15]. An intriguing question is whether there are other systems with long range interactions that can also exhibit a dynamical reversible to irreversible transition under periodic driving, and if there can be reversible states that are not simply random but form patterns or structures that differ from the initial random distributions. Dislocations undergoing glide in materials are a prime candidate system in which to address these questions. Under dc loading, the stress in materials containing dislocations increases with strain and levels off when yielding occurs and the material flows [16,17]. Numerous simulations show that dislocation patterning can occur under dc loading [18,19]. A true elastic regime usually occurs only for very low strains, while in the regime where the stress is increasing nonlinearly, plastic rearrangements occur. In general, plastic flow is thought of as always being irreversible; however, there are now examples of reversible flow of dislocations in what is called recovery when the system is driven in a single cycle [20,21]. Additionally, recent simulations of amorphous solids under periodic forcing have shown that just as in the dilute colloidal case, the system can begin in an irreversible plastic state and then settle into a reversible state with plastic rearrangements that repeat periodically, and that there is a critical amplitude above which the motion remains irreversible [22,23]. Experiments on periodically sheared jammed materials have also identified a reversible to irreversible transition [24], and numerical simulations have explored the connection between jamming and reversible-irreversible transitions [25].

Here we use large scale numerical simulations to examine the periodic forcing of gliding dislocations for different shear amplitudes with the stroboscopic measure developed for the dilute colloidal system. Our simulations are based on a well-established dislocation glide model that has previously been employed to study intermittency [26,27,28], avalanches [29], creep [19], hysteresis [30], jamming [17], and driven phases [31]. By comparing the dislocation positions from one drive cycle to the next, we can identify the number t_n of cycles required for the system to organize into a state where the dislocations return to the same position after each cycle. For low shear amplitude, the system quickly settles into a reversible state. For large loading, the dislocations pass each other so rapidly that they interact only weakly, and the system again quickly organizes to a reversible state. At a critical load τ_c, we find that t_n grows rapidly, similar to what is observed in the colloidal and vortex systems, and that t_n can be fitted to a power law with exponents consistent with those obtained in other systems [2,9,13,12]. Unlike the previously studied systems, our dislocation model always organizes to a reversible state both above and below τ_c, with a partially random reversible state appearing in the low drive regime, and a state with more well-defined wall structures occurring in the high drive regime.

2 Computational Details

We model dislocations in a two-dimensional (2D) system that are each confined to glide on parallel slip planes [26,19,17]. The motion of dislocation i depends on its Burgers vector, dislocation-dislocation interactions, and the external load according to the following equation of motion:

dx_i

= b_i

⎛
⎝

N
∑
j ≠ i

τ_int(r_j − r_i) − τ_ext

⎞
⎠

(1)

Here η is an effective damping constant that arises from dissipation mechanisms such as the radiation of phonons by dislocations, and the Burgers vector value b_i can be either positive or negative. The dislocations interact via an anisotropic stress field given by τ_int(r) = bμ[x(x² − y²)/(2π(1−ν)(x² + y²)²] where r = (x,y), μ is the shear modulus, and ν is the Poisson ratio. Here |b| = 1, η = 1.0, and μ/2π(1−ν) = 1.0. We use periodic boundary conditions, and treat the long-range dislocation interactions using a replicated image model [32,33]. The external load is τ_ext and the resulting dislocation motion is in either the positive or negative x-direction depending on the sign of the Burgers vector. We impose the rule that dislocations must be separated by a vertical distance no less than δy in order to avoid dislocation annihilation processes, and place only one dislocation on each glide plane. We measure the absolute value of the dislocation velocity v versus the external load. In previous work with this system, yielding and intermittent dynamics were studied under dc loads [19,17]. Here we consider the effects of periodic loading and compare the positions of the dislocations at the beginning and end of each load cycle. The external load τ_ext(t) = τ_extsgn(sin(2πt/P)) is a square wave with total amplitude 2τ_ext and period P measured in simulation time steps. Unless otherwise noted, we take P=2.5 ×10⁵. The fraction A_n of dislocations that do not return to the same position are labeled as active and identified by comparing the net dislocation displacement after n cycles with a small distance δx,

A_n = N_d⁻¹

N_d
∑
i = 1

Θ([X_i(t_n+1 ) − X_i(t_n)]² − δx) ,

(2)

where Θ is the Heaviside step function. We take δx=10⁻⁵; we have tried various other cutoffs and find that smaller values of δx give the same results. When the system is in a reversible regime, A_n = 0.0. We consider systems containing up to 480 dislocations with equal numbers of positive and negative Burgers vectors. The dislocations are allowed to relax for a fixed time before the external driving is applied. In general the system always shows an initial irreversible dynamics during the first few cycles, as also observed in the colloidal suspensions [2] and vortex experiments [9].

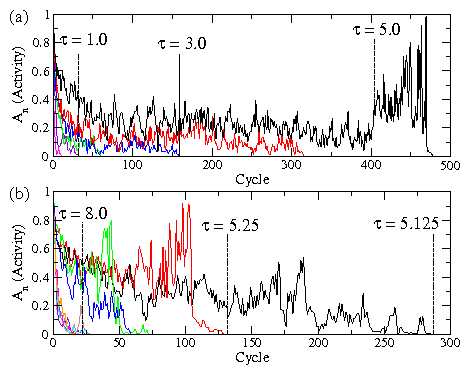
Figure 1: (a) The fraction of active dislocations A_n that do not return to the same position after n successive cycles of a periodic drive, plotted vs n. When A_n = 0, the system is considered reversible. From left to right, the external drive τ_ext = 0.5, 1.0, 2.0, 3.0, 4.0, and 5.0. The τ_ext = 1.0, 3.0 and 5.0 curves are highlighted to show that the transient times increase with increasing τ_ext. (b) The same for τ_ext = 5.125, 5.25, 5.5, 6.0, 8.0, and 9.0, with the τ_ext = 5.125, 5.25, and 8.0 curves marked to show that the transient times are now decreasing with increasing τ_ext.

Figure 2: (a) t_n, the number of cycles required to reach a reversible state, vs drive amplitude τ_ext. Here t_n passes through a maximum at finite τ_ext. The dashed lines are fits to |τ_c − τ_ext|^β with τ_c = 4.75 and β = 1.375. (b) A log-log plot of t_n vs drive amplitude τ_ext−τ_c for the regime where τ > τ_c. The drive period is P=3.0 ×10⁵ (squares), 2.5 ×10⁵ (circles), 2.0 ×10⁵, (triangles) and 1.5 ×10⁵ (diamonds). The dashed line is a power law fit with β = 1.375.

3 Results and Discussion

3.1 Transient times

Under a small external dc strain, the velocities settle to zero so that the material can be said to be jammed or below yield. As the dc external drive is increased, there is a critical yield load at which the velocity always remains finite; above this load, the system is beyond the yield point [34]. From dc measurements with a slowly increasing external load, a well defined yield point τ_c can be obtained that increases as either 1/√(ρ) [17] or 1/ρ for increasing dislocation density ρ. In Fig. 1(a) we plot A_n vs n for a system with a fixed frequency periodic drive for different values of τ_ext = 0.5 to 5.0. We highlight the transient times t_n for drives τ_ext=1.0, 3.0, and 5.0 to show that t_n increases with increasing τ_ext. Here, A_n for τ_ext = 0.5 drops to zero after only n=10 cycles, while for τ_ext = 5.0, reversibility does not appear until after n=480 cycles. Figure 1(b) shows A_n for τ_ext = 5.125, to 9.0 with the drives at τ_ext=5.125, 5.25, and 8.0 labeled to indicate that t_n is now decreasing with increasing τ_ext. This result indicates that there is a peak in t_n centered around a critical amplitude τ_c.

In Fig. 2(a) we plot the transient time t_n vs τ_ext to more clearly show the divergence in t_n just below τ_ext=5.0. In the colloidal work, the transient times also showed a divergence centered at a critical drive amplitude that was fit to a power law form [2]. In Fig. 2(a), the lines are fits to t_n ∝ |τ_ext − τ_c|^−β with β = 1.375 and τ_c = 4.75. The fit of the data is best for τ_ext > 4.75. For the 2D dilute suspension simulations, similar fits gave β = 1.33 [2], while the 3D experiments gave β = 1.1 [2]. Experiments on periodically sheared superconducting vortex systems using the same fitting produced β = 1.3 [9]. For simulations of dc depinning in the plastic regime, a diverging time scale at a critical depinning force was found with β = 1.37 [12], while experiments on dc driven superconducting vortices gave β = 1.6 [13] and β = 1.4 [9]. In Fig. 2(b) we plot log-log fits of t_n vs (τ−τ_c) for varied drive periods P=3.0 ×10⁵, 2.5 ×10⁵, 2.0 ×10⁵, and 1.5 ×10⁵ for τ_ext > τ_c with τ_c = 4.75. The dashed line is a fit to β = 1.375. The fit breaks down for large τ_ext, as expected since critical phenomena should only occur near τ_c. Although our results are not able to provide a highly accurate exponent, they show that our system exhibits the same general trends found for the random organization observed in other systems, with the exponents in reasonable agreement. This suggests that all these systems exhibit nonequilibrium dynamical phase transitions in the same universality class.

Figure 3: (a) t_n vs cycle period P for τ_ext = 8.0 (diamonds), 5.0 (circles), 3.0 (squares), and 1.0 (triangles). (b) The net burgers vector b_net along quasi-1D stripes vs τ_ext for a system with P=2.5×10⁵. For τ_ext > τ_c, the system starts to form domain walls.

In Fig. 3 we examine how the transient times t_n change for a fixed periodic drive amplitude but with increasing drive period P. We find that the value of τ_ext at which the divergence occurs is independent of P; however, near τ_c the transient times increase with increasing P. In Fig. 3(a) at τ_ext = 3.0 and τ_ext = 8.0, t_n remains constant for increasing P, while for τ_ext = 5.0 there is a strong increase in t_n with increasing P. At τ_ext = 3.0 there is also a weaker increase in t_n with increasing P. This result suggests that for very long drive cycle period, the divergence in t_n will become more pronounced.

One clear difference between the dislocation system and the simulations of sheared dilute colloidal particles is that the gliding dislocations always evolve into a reversible state, whereas the colloidal system remains in a steady irreversible state at large drives. This may be a result of the fact that in the dislocation model we employ, even though the interactions are 2D, the dislocations are confined to move only along 1D lines [26,19]. In the colloidal system, the particles can move in the 2D continuum, permitting the formation of many more possible states. In the superconducting vortex system, the vortices can freely move in the 2D plane and there is again a transition to a steady irreversible state at high enough drive [8]. For more complicated dislocation dynamics models that incorporate both climb and glide, it may be possible for the system to remain irreversible above the critical amplitude. It was proposed in the colloidal shearing work and the driven vortex systems that the transition from the reversible to the irreversible state is a nonequilibrium phase transition or an absorbing phase transition which may fall in the universality class of directed percolation or conserved directed percolation [2,7]. The exponents that have been reported in these systems are consistent with this scenario, although it has not been possible to distinguish between the two classes since their exponents are nearly identical. In our system, the divergence in t_n suggests that a nonequilibrium phase transition occurs that is similar to that found in the colloidal system, and that the dislocation system organizes into two different absorbing states on either side of the transition. In real experiments, additional effects such as climb may occur that could change the nature of the transition.

Figure 4: Dislocation positions, with the different shadings corresponding to the two different Burgers vectors. (a) The undriven case showing a random spatial distribution of dislocations. (b) At τ_ext = 4.0 and P=2.5 ×10⁵ time steps, the system forms a disordered configuration with a small number of wall-type structures.

Although the high and low drive states in the dislocation system cannot be distinguished by whether they are dynamically reversible or not, they do have different spatial dislocation structure properties. Figure 4(a) shows that the dislocation positions without any external driving are strongly disordered. When the system reaches a reversible state for τ_ext < τ_c, the dislocations still have a disordered spatial pattern; however, there are small regions where wall-like structures form, as illustrated in Fig. 4(b) for the reversible regime at τ_ext = 4.0. For τ_ext > τ_c, the system forms a larger number of wall structures.

To characterize the change in the dislocation structures across the critical drive, we measure the fraction of dislocations P_b that are contained in walls by measuring the net Burgers vectors along thin y-direction strips of the system. For random dislocation distributions in the regime τ_ext < τ_c, P_b is close to zero, while for τ_ext > τ_c, P_b jumps up to a much higher value. This result shows that the dislocations do not necessarily organize into a random state, as found for the colloidal systems [2]; instead, for τ_ext > τ_c they can organize into an absorbing pattern-forming state. This suggests that the protocol of periodic forcing followed by a measurement of the time required for the system to organize into a dynamically reversible state might be fruitfully applied to a much wider class of systems, including many pattern forming systems. For example, in driven twin boundaries, magnetic domain walls, and binary mixtures, one reversible state could be a random or disordered pattern while the other reversible state could be spatially ordered.

4 Conclusion

In summary, we have examined the dynamics of periodically driven gliding dislocations in 2D simulations. We find that this system exhibits many of the same features observed for random organization of periodically sheared colloidal particle suspensions, granular media, and superconducting vortices. The system is initially irreversible with the dislocations returning to different positions after each driving cycle, but over time it organizes into a reversible state where the dislocations return to the same positions after each drive cycle. The transient time required to reach a reversible state shows a divergence at a critical load near the dc yield point, and the exponents of the divergence are consistent with those found for the colloidal assemblies, suggesting that the dislocation system may exhibit a nonequilibrium phase transition of the same university class as the diluted colloidal systems. One difference from previous studies is that the dislocation system always organizes into a reversible state, whereas the other systems remain in an irreversible state above a critical driving amplitude. The two reversible states into which the dislocations organize are characterized by different patterns on either side of the critical load. For smaller loads, the system organizes into a more random state of small walls, while above the critical load, the system organizes into states with partial wall structures. Future directions would be to add more complicated dislocation dynamics such as cross slip and climb, which could change one of the reversible phases into an irreversible state that more closely resembles that found in the periodically driven colloidal system.

This work was carried out under the auspices of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]: D.J. Pine, J.P. Gollub, J.F. Brady, and A.M. Leshansky, Nature 438, 997 (2005).
[2]: L. Corte, P.M. Chaikin, J.P. Gollub, and D.J. Pine, Nature Phys. 4, 420 (2008).
[3]: D. Frenkel, Nature Phys. 4, 345 (2008).
[4]: A. Franceschini, E. Filippidi, E. Guazzelli, and D.J. Pine, Phys. Rev. Lett. 107, 250603 (2011).
[5]: B. Metzger and J.E. Butler, Phys. Rev. E 82, 051406 (2010); Phys. Fluids 24, 021703 (2012).
[6]: J.S. Guasto, A.S. Ross, and J.P. Gollub, Phys. Rev. E 81, 061401 (2010).
[7]: H. Hinrichsen, Adv. Phys. 49, 815 (2000).
[8]: N. Mangan, C. Reichhardt, and C.J. Olson Reichhardt, Phys. Rev. Lett. 100, 187002 (2008).
[9]: S. Okuma, S. Tsugawa, and A. Motohashi, Phys. Rev. B 83, 012503 (2011).
[10]: W. Zhang, W. Zhou, and M.B. Luo, Phys. Lett. A 374, 3666 (2010).
[11]: D. Perez Daroca, G. Pasquini, G.S. Lozano, and V. Bekeris, Phys. Rev. B 84, 012508 (2011).
[12]: C. Reichhardt and C.J. Olson Reichhardt, Phys. Rev. Lett. 103, 168301 (2009).
[13]: G. Shaw, P. Mandal, S.S. Banerjee, A. Niazi, A.K. Rastogi, A.K. Sood, S. Ramakrishnan, and A.K. Grover, Phys. Rev. B 85, 174517 (2012).
[14]: S. Okuma and A. Motohashi, New J. Phys. 14, 123021 (2012).
[15]: Y. Fily, E. Olive, N. Di Scala, and J.C. Soret, Phys. Rev. B 82, 134519 (2010).
[16]: M. Zaiser, Adv. Phys. 55, 185 (2006).
[17]: G. Tsekenis, N. Goldenfeld, and K.A. Dahmen, Phys. Rev. Lett. 106, 105501 (2011).
[18]: J. Lepinoux and L.P. Kubin, Scripta Metall. 21, 833 (1987); A. Gulluoglu, D.J. Srolovitz, and P.S. Lomdahl, J. Metals 40, A6 (1988). I. Groma and G.S. Pawley, Phil. Mag. A 67, 1459 (1993).
[19]: M.-C. Miguel, A. Vespignani, M. Zaiser, and S. Zapperi, Phys. Rev. Lett. 89, 165501 (2002).
[20]: J. Rajagopalan, H.H. Han, M. Taher, and A. Saif, Science 315, 5280 (2007).
[21]: X. Li, Y. Wei, W. Yang, and G. Gao, Proc. Nat. Acad. Sci. (USA) 106, 16108 (2009).
[22]: I. Regev, T. Lookman, and C. Reichhardt, arXiv:1301.7479.
[23]: D. Fiocco, G. Foffi, and S. Sastry, Phys. Rev. E 88, 020301 (2013).
[24]: N.C. Keim and P.E. Arratia, Soft Matter 9, 6222 (2013); N.C. Keim, P.E. Arratia arXiv:1308.6806.
[25]: C.F. Schreck, R.S. Hoy, M.D. Shattuck, and C.S. O'Hern, arXiv:1301.7492.
[26]: M.-C. Miguel, A. Vespignani, S. Zapperi, J. Weiss, and J.R. Grasso, Nature (London) 410, 667 (2001).
[27]: P.D. Ispanovity, I. Groma, G. Gyorgyi, P. Szabo, and W. Hoffeiner, Phys. Rev. Lett. 107, 085506 (2011).
[28]: S. Papanikolaou, D.M. Dimiduk, W. Choi, J.P. Sethna, M.D. Uchic, C.F. Woodward, and S. Zapperi, Nature 490, 517 (2012).
[29]: D.M. Dimiduk, C. Woodward, R. LeSar and M.D. Uchic, Science 312, 1188 (2006).
[30]: L. Laurson and M.J. Alava, Phys. Rev. Lett. 109, 155504 (2012).
[31]: C. Zhou, C. Reichhardt, C.J.O. Reichhardt, and I.J. Beyerlein, arXiv:1207.6657.
[32]: J.P. Hirth and J. Lothe, Theory of Dislocations (Wiley, New York, 1982).
[33]: A.N. Gulluoglu, D.J. Srolovitz, R. LeSar, and P.S. Lomdahl, Scripta Metall. 23, 1347 (1989).
[34]: E. Lerner and I. Procaccia, Phys. Rev. E 80, 026128 (2009); S. Karmakar, E. Lerner, I. Procaccia, and J. Zylberg, Phys. Rev. E 83, 046016 (2011).

File translated from T_EX by T_THgold, version 4.00.
Back to Home