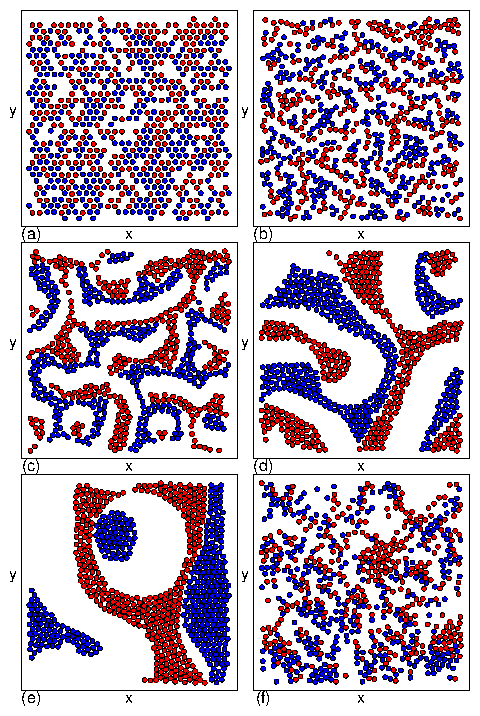
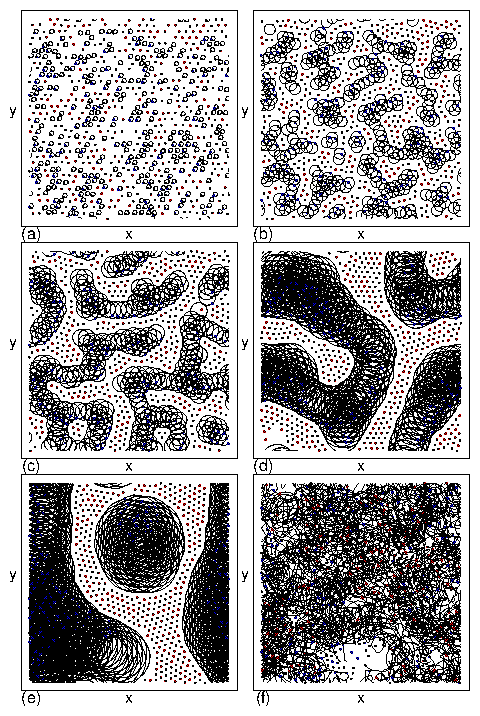
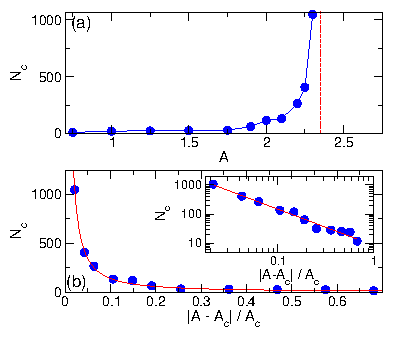
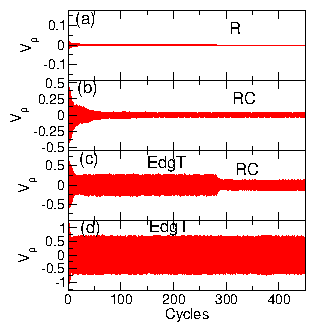
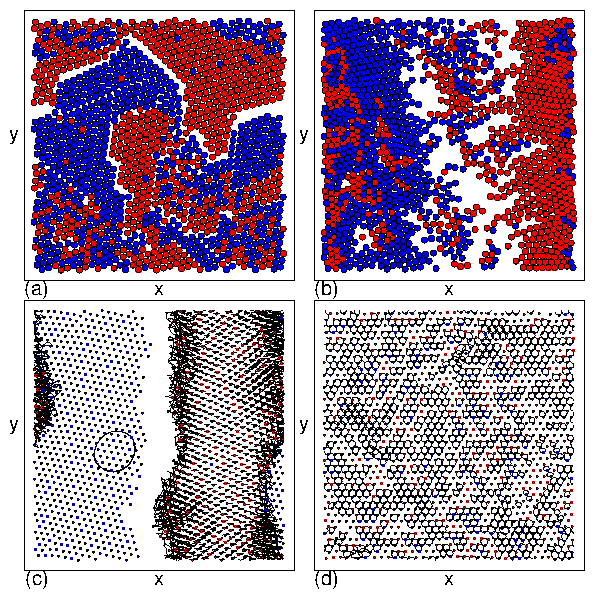
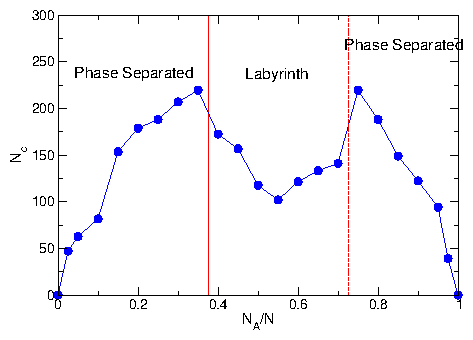
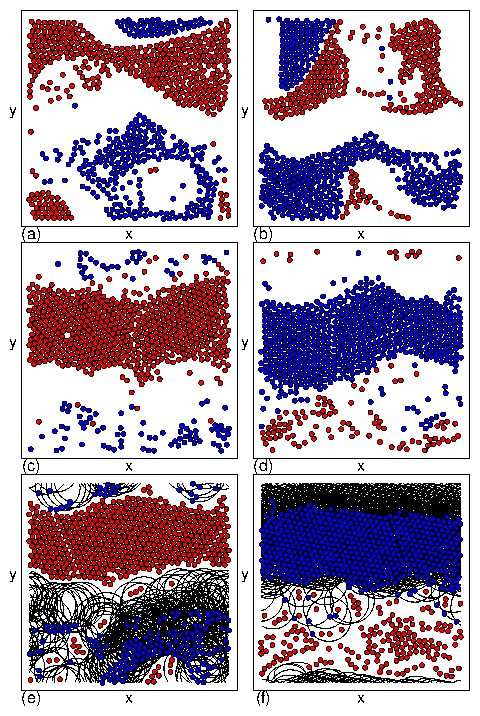
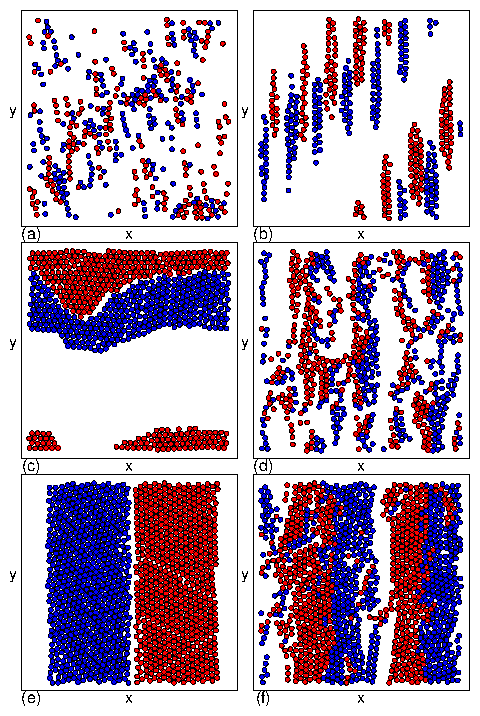
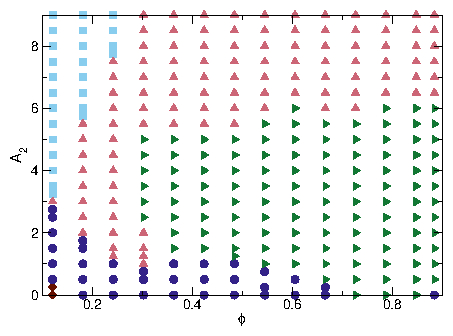
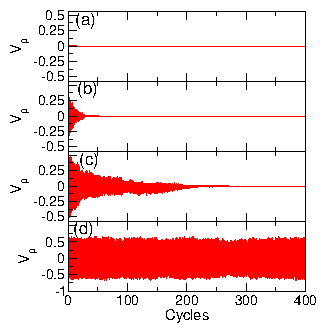
 Figure 1:
Vp, the instantaneous x-component velocity of the passive disks,
vs time in circular drive cycles
for a binary assembly of disks
in a system with a total disk density of ϕ = 0.424 where
half of the disks
are driven in a circular motion and the other half are passive.
(a) At a circular drive amplitude of A = 0.2,
the system
is always in a collision-free state
as indicated by the fixed value of Vp = 0.0.
(b) At A = 1.5,
Vp is initially finite due to the occurrence of disk-disk
collisions,
but drops to zero
after 30 cycles.
(c) At A = 2.2, the system requires 250 cycles to reach a
collision-free state with Vp=0.
(d) At A = 2.75,
the system remains in a fluctuating state with continuous
disk-disk collisions.
Figure 1:
Vp, the instantaneous x-component velocity of the passive disks,
vs time in circular drive cycles
for a binary assembly of disks
in a system with a total disk density of ϕ = 0.424 where
half of the disks
are driven in a circular motion and the other half are passive.
(a) At a circular drive amplitude of A = 0.2,
the system
is always in a collision-free state
as indicated by the fixed value of Vp = 0.0.
(b) At A = 1.5,
Vp is initially finite due to the occurrence of disk-disk
collisions,
but drops to zero
after 30 cycles.
(c) At A = 2.2, the system requires 250 cycles to reach a
collision-free state with Vp=0.
(d) At A = 2.75,
the system remains in a fluctuating state with continuous
disk-disk collisions.
|