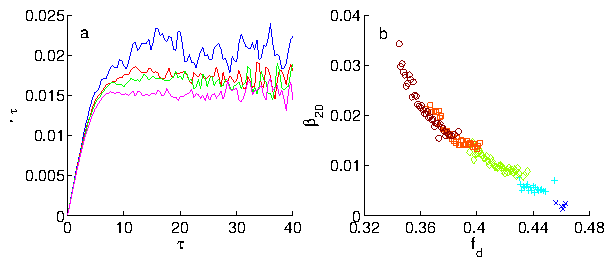
 Figure 5:
(a) Nonequilibrium temperature
βτ in a nonthermal system with quenched
disorder at
fd=0.335,
0.340,
0.345,
and 0.350
(from top to bottom).
In all cases βτ relaxes to the intrinsic noise level
within τ <~10.
(b) β20=〈β15 < τ < 25〉
vs
fd for
ρ = 0.1 (x),
0.2 (+), 0.3 (\Diamond), 0.5 ([¯]), and 0.6 (\bigcirc).
Figure 5:
(a) Nonequilibrium temperature
βτ in a nonthermal system with quenched
disorder at
fd=0.335,
0.340,
0.345,
and 0.350
(from top to bottom).
In all cases βτ relaxes to the intrinsic noise level
within τ <~10.
(b) β20=〈β15 < τ < 25〉
vs
fd for
ρ = 0.1 (x),
0.2 (+), 0.3 (\Diamond), 0.5 ([¯]), and 0.6 (\bigcirc).
|