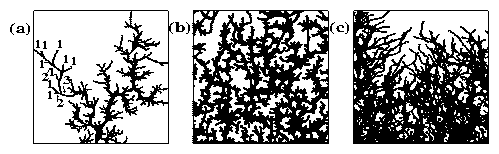
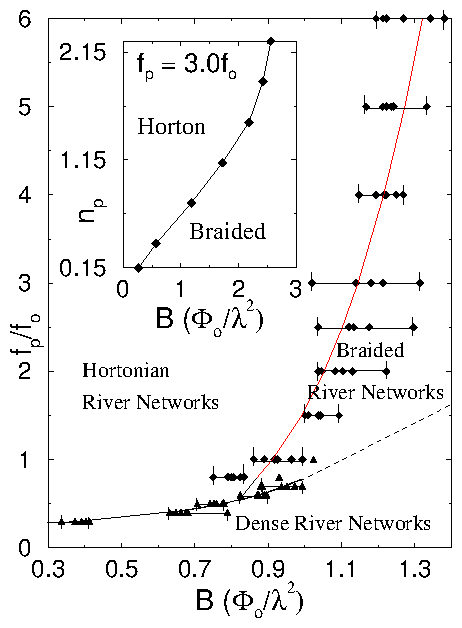
 Figure 2: The vortex river network morphological
phase diagram for pinning force, fp, versus
magnetic field, B, for np=0.75/λ2
(thus, here Bϕ = 0.75 Φ0 / λ2).
In regions of very low pinning force, dense
vortex river networks dominate.
For higher pinning fp's, the Hortonian
rivers become braided when B grows.
For samples with significant amount of pinning, it is
the initial front (with low local density of
field lines B, B < 3 Bϕ / 2 [7],
and thus dominant pinning force fp) which branches
out in a Hortonian manner. Behind this initial front
follows the (intermediate-B) braided region. Further
behind, follows the (large-B) dense-flux regime.
The inset shows the shift in the
Horton-braided boundary fp=3.0f0
as the pinning density, np, is changed.
As np is increased, the Horton-braided
boundary shifts towards higher B.
The broad crossover boundaries are in the region of triangles and
rhombuses. The (power-law-fit) lines are just guides to the eye.
The dense-braided crossover at high-fields (dashed)
is an extrapolation of the power-law-fit for low fields;
the former is very difficult to compute because it requires
a large number of vortices monitored over very long times.
Figure 2: The vortex river network morphological
phase diagram for pinning force, fp, versus
magnetic field, B, for np=0.75/λ2
(thus, here Bϕ = 0.75 Φ0 / λ2).
In regions of very low pinning force, dense
vortex river networks dominate.
For higher pinning fp's, the Hortonian
rivers become braided when B grows.
For samples with significant amount of pinning, it is
the initial front (with low local density of
field lines B, B < 3 Bϕ / 2 [7],
and thus dominant pinning force fp) which branches
out in a Hortonian manner. Behind this initial front
follows the (intermediate-B) braided region. Further
behind, follows the (large-B) dense-flux regime.
The inset shows the shift in the
Horton-braided boundary fp=3.0f0
as the pinning density, np, is changed.
As np is increased, the Horton-braided
boundary shifts towards higher B.
The broad crossover boundaries are in the region of triangles and
rhombuses. The (power-law-fit) lines are just guides to the eye.
The dense-braided crossover at high-fields (dashed)
is an extrapolation of the power-law-fit for low fields;
the former is very difficult to compute because it requires
a large number of vortices monitored over very long times.
|