Physical Review E 84, 011303 (2011)

Jamming in Granular Polymers

L. M. Lopatina, C. J. Olson Reichhardt, and C. Reichhardt

Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 9 December 2009; revised manuscript received 8 April 2011; published 18 July 2011)

We examine the jamming transition in a two-dimensional granular polymer system using compressional simulations. The jamming density ϕ_c decreases with increasing length of the granular chain due to the formation of loop structures, in excellent agreement with recent experiments. The jamming density can be further reduced in mixtures of granular chains and granular rings, also as observed in experiment. We show that the nature of the jamming in granular polymer systems has pronounced differences from the jamming behavior observed for polydisperse two-dimensional disk systems at Point J. This result provides further evidence that there is more than one type of jamming transition.

Jamming, or the development of a resistance to shear, is a phenomenon that occurs when a disordered assembly of particles subjected to increasing density, load or other perturbations exhibits a transition from a liquid-like state that can flow to a rigid state that acts like a solid under compression. Tremendous recent growth in this field has been driven by the prospect that jamming may be associated with universal properties across a wide class of systems including granular media, foams, emulsions, colloids, and glass forming materials [1]. One of the most accessible routes for exploring the jamming transition is gradually increasing the density of a sample in the absence of shear or temperature. Here, jamming occurs at a density termed `Point J.' [2]. Jamming transitions have been studied both for noncohesive granular media and for cohesive and/or nonspherical granular materials [3,4,5,6]. There is considerable evidence that for frictionless disordered disk assemblies, critical behavior occurs near Point J, with both the pressure and the particle coordination number Z exhibiting power law behavior as a function of packing density ϕ [2,7,8,9]. Similar behavior appears when the shear, external forcing, or temperature are finite, providing further evidence that the jamming transition may indeed exhibit universal properties [10,11,12,13,15,14,16]. If such universal behavior holds for other systems that undergo jamming, it would have profound implications for the understanding and control of disordered and glassy systems.

The most widely studied two-dimensional (2D) jamming system contains bidisperse frictionless disks. When two sizes of disks with a radius ratio of 1:1.4 are mixed in a 50:50 ratio, a jamming transition occurs at a density of ϕ = 0.84 [2,9,10,11,12,15,16]. To explore whether the jamming transition is universal in nature, it would be ideal to have a system in which the jamming density ϕ_c could be tuned easily. Here we propose that one model system which meets this criterion is an assembly of 2D granular polymers. This model is motivated by experiments on granular polymers or chains of the type used for lamp pulls, where various aspects of knot formation, diffusion processes, and pattern formation have been explored [17,18,19]. We model the chains as coupled harmonically repulsive disks similar to those studied in the polydisperse disk system, with a constraint on the minimum angle that can be spanned by a string of three disks. Other workers have considered freely-jointed chains [20] or chains of sticky spheres [21]. Although our model is 2D and neglects friction, we show that it captures the same features found in recent three-dimensional (3D) granular polymer compaction experiments [22,23]. To study the jamming transition, we construct pressure versus ϕ curves by compressing the chains between two walls, and compare our results to compression experiments on 2D polydisperse disks [9,17]. We show that the jamming density ϕ_c decreases with increasing chain length and saturates at long chain lengths, in agreement with the experiments of Ref. [22]. The decrease of ϕ_c occurs due to the formation of rigid loops along the chains which stabilize voids inside the packing. Unlike the bidisperse disk system where the pressure scales nearly linearly with ϕ, in the chain system the pressure increases with a power law form with an exponent significantly larger than 1 as the jamming transition is approached. Jamming of our frictionless granular chains shares several features with jamming of frictional disks and could be distinct from the jamming transition for frictionless disks.

We simulate a 2D system confined by two walls at x=0 and x=L and with periodic boundaries in the y direction. The wall at x=L is held fixed while the position of the other wall is allowed to vary in order to change the density. The system contains N chains or loops, each of which is composed of M_b individual disks that are strung together by harmonic springs and that experience a constraining force which limits the bending radius of the chain. In loops, the two ends of a chain are connected together. The disk-disk interaction is modeled as a stiff harmonic repulsion, and the motion of all disks is taken to be overdamped in order to represent the frictional force between the disks and the underlying floor. A given disk i moves according to the following equation of motion:

d R_i

= F_ddⁱ + F_cⁱ + F_ccⁱ +F_wⁱ.

(1)

Here we take the damping constant η = 1. The disk-disk interaction potential is F_ddⁱ=∑_{j ≠ i}^NM_bk_g(r_eff−r_ij)Θ(r_eff−r_ij)∧r_ij where the spring constant k_g=300, r_ij=|R_i−R_j|, ∧r_ij=(R_i−R_j)/R_ij, Θ is the Heaviside step function, and r_eff=r_i+r_j, where r_i(j) is the radius of disk i(j). For the chains and loops we set r_i=1; for a bidisperse disk system we set r_i=1 for half of the disks and r_i=1.4 for the other half of the disks. The chain interaction potential is F_cⁱ=∑_kk_g(r_eff−r_ik)∧r_ik, and it acts only between a disk and its immediate neighbors along the loop or chain. The bending constraint potential F_ccⁱ=∑_lk_g(r_stiff−r_il)Θ(r_stiff−r_il)∧r_il acts between disks separated by one chain element, with r_stiff=2r_effsin(θ_s/2) and θ_s=0.82π unless otherwise noted. Smaller values of θ_s produce more bendable chains. The disk-wall interaction force F_wⁱ is computed by placing a virtual disk at a position reflected across the wall from the actual disk, and finding the resulting disk-disk force. To initialize the system, we place the chains, rings, or individual disks in random non-overlapping positions to form a low density unjammed phase, such as in Fig. 1(a). The x=L wall is held fixed while the other wall is gradually moved from x=0 to larger x in small increments of δx. The waiting time between increments is taken long enough so that the system has sufficient time to relax to a state where the velocities of all particles are indistinguishable from zero.

Figure 1: (Color online) Granular configurations in a portion of the sample. The x direction runs vertically and the fixed wall is at the top of each panel. (a) An unjammed system of N=67 granular polymers with length M_b = 16. (b) The jammed configuration for the same system contains voids which appear when the chains form ring structures. (c) The jammed configuration for N=67 loops of length M_b = 16. The jamming density is lower than for systems of chains or individual disks. (d) The jammed configuration at ϕ = 0.84 for a sample of N=1500 bidisperse frictionless disks contains no significant voids.

We identify the jamming transition by measuring the total force exerted on the fixed wall by the packing, P=∑_i^NM_bF_wⁱ ·∧x, and the average contact number Z=(NM_b)⁻¹∑_i^NM_bz_i as a function of the total density of the system defined by the spacing between the two walls. To determine the contact number z_i of an individual grain in a chain, we first count the immediate neighbors of the grain along the chain, and then add any other grains that are in contact with the individual grain. The force P is proportional to the p_xx component of the pressure tensor. At the jamming transition, the pressure in the system becomes finite [2,7,9], while below jamming P=0. Previous simulations on 2D disordered disk packings have revealed the onset of a finite pressure near ϕ_c = 0.84 which grows as P ∝ (ϕ− ϕ_c)^ψ with ψ = α_f −1, where α_f is the exponent of the interparticle interaction potential [2,7]. Recent work which includes careful corrections to scaling indicates that the exponent ψ = 1.1 [24]. Theoretical work on the jamming of 2D disks also predicts a power law scaling of the pressure versus density [8], and indicates that the contact number Z should scale as Z ∝ (ϕ− ϕ_c)^β, with β = 0.5. Experiments using a combination of shear and compression on the same disk system found that after performing cycling to reduce the effect of friction, the pressure and Z both scale with the density as power laws with ψ = 1.1 and β = 0.495 [9].

Figure 2: (a) The pressure P vs ϕ for a bidisperse disk system. Above the jamming transition at ϕ ≈ 0.84, P increases nearly linearly with ϕ. (b) P vs ϕ for the granular polymer system with chains of length M_b=6 (black down triangles), 8 (big up triangles), 10 (black lozenges), 16 (squares), and 24 (•). As M_b increases, the onset of a finite value of P indicating jamming drops to lower values of ϕ and the near linear scaling of P with ϕ is lost.

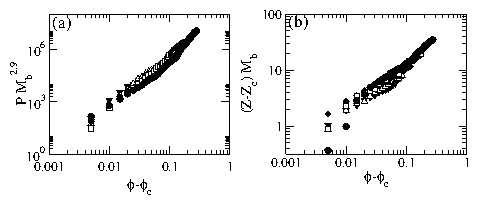
Figure 3: (a) Scaling of pressure vs density, P M_b^2.9 vs ϕ−ϕ_c close to the jamming transition for chains of length M_b=6 (black down triangle), 8 (big up triangle), 10 (black lozenge), 16 (square), and 24 (•). (b) Scaling of (Z−Z_c) M_b vs ϕ−ϕ_c for chains of length M_b=6, 8, 10, 16, and 24, with the same symbols as in panel (a).

Figure 4: (a) Contact number Z vs ϕ for chains of length M_b=6 (black triangle down), 8 (big up triangle), 10 (black lozenge), 16 (square), and 24 (•). (b) Bulk pressure tensors p_xx (big circle) and p_yy (black lozenge) vs ϕ for M_b=16.

Figure 5: (Color online) The shear velocity V_shear of grains adjacent to the stationary wall vs ϕ (dark black symbols) and the corresponding pressure P in the packing vs ϕ (light red symbols) for a sample in which a shear force is applied using the mobile wall with chain lengths M_b=6 (black triangle down), 8 (big up triangle), 10 (black lozenge), 16 (square), and 24 (•). The onset of a finite pressure and a finite shear response occur at the same value of ϕ for each sample.

We first test our simulation geometry using the bidisperse individual disk system. A configuration of N=1500 disks appears in Fig. 1(d) just above the onset of a finite pressure P at ϕ ≈ 0.84. In Fig. 2(a) we show that for the disk system above jamming, P increases nearly linearly with ϕ, consistent with a scaling exponent ψ = 1.1 ±0.1. This indicates that our compressional geometry captures the jamming behavior found in other studies of bidisperse disks.

We use the same compression protocol to study the jamming behavior of granular polymers, as illustrated in Fig. 1(a,b) for a system with N=67 chains that are each of length M_b = 16. In Fig. 2(b) we plot P versus ϕ for granular polymer chains of lengths M_b=6, 8, 10, 16, and 24. For the chains, the onset of finite P indicating the beginning of jammed behavior occurs at a much lower density than for the bidisperse disk system shown in Fig. 2(a), and as M_b increases, the jamming transition shifts to even lower ϕ and the nearly linear dependence of P on ϕ is lost. We illustrate scaling of P near the jamming transition in Fig. 3(a) where we plot P M_b^2.9 vs ϕ−ϕ_c. Here we find ψ ≈ 3. The jammed state develops isotropic rigidity, as indicated by the plot of the bulk pressure tensor components p_xx and p_yy in Fig. 4(b). To test whether the packing also develops a finite response to shear at the jamming transition, we fix the packing density and apply a shear to the system by applying a force F_shear=0.04∧y to all particles that are in contact with the mobile wall. We measure the resulting steady state velocity V_shear=dR_i/dt ·∧y of all particles that are in contact with the stationary wall on the other side of the sample, discarding any brief initial transient responses. In Fig. 5 we plot V_shear and P versus ϕ for samples with chains of length M_b=6, 8, 10, 16, and 24. In each case, a finite shear response and a finite pressure P appear simultaneously at the jamming density. Our use of a fixed F_shear at all densities rather than a variable shear rate affects the shape of the V_shear versus ϕ curves; variations in the shear rate as well as related hysteretic effects under shear will be the subject of a future publication.

Figure 6: (Color online) (a) The jamming threshold ϕ_c versus chain length M_b for chains with a bending angle of θ_s=0.82π (circles) and θ_s=0.756π (squares). ϕ_c decreases with increasing M_b and saturates at large M_b. Inset: ϕ_c vs θ_s for a system with M_b = 16. (b) ϕ_c vs chain fraction N_c/N for a system with M_b = 16 and a mixture of loops and chains. As the fraction of chains decreases, ϕ_c decreases.

We define the jamming threshold ϕ_c as the density at which P rises to a finite level. The same threshold also appears as the sudden onset of an increase in Z, as seen in Fig. 4(a). The scaling of (Z−Z_c) M_b vs ϕ− ϕ_c appears in Fig. 3(b), where the exponent β falls in the range β = 0.6 to 0.8. In Fig. 6 we plot ϕ_c versus M_b for chains of two different stiffnesses: θ_s=0.82π and θ_s=0.756π. In both cases, ϕ_c decreases monotonically with increasing M_b and saturates for large M_b. Recent experiments on the packing of granular polymers showed the same behavior: the final packing density decreased for increasing chain length and saturated for very long chains [22]. This was attributed to the formation of rigid semiloops which stabilized voids in the packing and decreased the jamming density. Loops have also been observed in dense 3D packings of freely-jointed chains [25]. Since the minimum area spanned by a semiloop increases with θ_s, the jamming density should be lower for larger θ_s when larger voids are stabilized. Figure 1(b) illustrates the voids that appear in our chain packings due to the formation of rigid semiloops. For comparison, the bidisperse disk system shown in Fig. 1(d) contains no large voids. If the rattler disks in Fig. 1(d) were removed, the amount of void space present would increase, but the chain system would still be able to stabilize a larger amount of void space since the constraint of the chain backbone permits the formation of larger arches around the voids than the arches that can be stabilized in the bidisperse disk system. The semiloops increase in size for increasing θ_s and ϕ_c is reduced at higher θ_s, as shown in Fig. 6(a). The plot of ϕ_c versus θ_s in the inset of Fig. 6(a) for fixed M_b=16 shows that ϕ_c monotonically decreases with increasing θ_s. For perfectly flexible chains with θ_s=0, we find ϕ_c ≈ 0.8. This is lower than the density of a triangular lattice due to the trapping of voids within the packing by the physical constraints of the bonding between chain elements. If the system were annealed or shaken for a sufficiently long time, these voids could eventually be freed and the perfectly flexible chains would form a perfect triangular lattice.

As a confirmation of the idea that the formation of rigid semiloops is the mechanism by which the jamming density is depressed, Ref. [22] includes experiments performed on mixtures of granular polymers and granular loops with equal length M_b. In this case, ϕ_c decreased linearly as the fraction of loops increased. We find the same effect in our 2D system by varying the number of loops N_l and chains N_c in a sample with fixed N=N_l+N_c and fixed M_b. In Fig. 6(b) we plot ϕ_c versus N_c/N, where N_c/N=1 indicates a sample containing only chains and N_c/N=0 is a sample containing only loops. As N_c/N decreases, ϕ_c decreases. The jammed configuration for a sample with M_b=16 containing only loops, N_c/N=0, appears in Fig. 1(c). The number of voids present is much larger than in the N_c/N=1 sample shown in Fig. 1(b). Interestingly, the voids began to form a disordered triangular packing.

Our results indicate that the experimentally observed dependence of the jamming density on chain length or fraction of loops in Ref. [22] is not caused by friction or other possible spurious effects, but is instead a product of the geometrical configuration of the chains and loops. The surprisingly good agreement between our 2D simulations and the 3D experiments may be due to the fact that in each case, the semiloops formed by the chains are 2D in nature. Additionally, in the experiment the container used to hold the sample induced ordering of the chains and loops near the walls and may have caused the system to act more two-dimensional. The fact that much of the physics observed for the 3D system can be captured in 2D models means that 2D experiments, which are much easier to image than 3D experiments, could provide many of the same insights for understanding jamming in a system where the jamming density can be tuned easily.

Figure 7: (Color online) (a) P vs ϕ for a chain sample with M_b = 20 on a log-linear scale. Light red line: initial compression; heavy black line: steady state reached after four compressions. (b) P vs ϕ for a system with M_b = 38 for the initial compression (light red line) and for the fourth compression (heavy black line). The response is hysteretic but the curves remain nonlinear on all compressions. Inset: A portion of the P vs ϕ curve during the second compression cycle in the same sample showing a sudden pressure drop associated with the collapse of an unstable void.

The chain system exhibits a pronounced hysteresis effect that can be seen by cycling the mobile wall in and out to repeatedly compress and uncompress the packing. Figs. 7(a) and (b) show a comparison of the responses during the first compression and during the fourth compression. After four compressions the system does not exhibit further hysteresis. In contrast, we find little or no hysteresis for the bidisperse disk system. During the initial compression, the chain systems often exhibit sizable fluctuations in P above the onset of jamming. Sudden drops in the pressure, such as that shown in the inset of Fig. 7(b), occur due to the collapse of semiloops that are larger than the minimum stable size. After all semiloops have reached a stable size, we find no further hysteresis. Even after cycling to a steady state, the P vs ϕ curves remain power law in nature with an exponent significantly larger than 1 and do not become linear or nearly linear. Simulations of compressed 2D frictional bidisperse disk systems show that void structures can form during the initial compression but collapse during subsequent cycles, allowing the sample to reach the same density as a frictionless disk sample [26]. In the chain system, the void structures are associated with semiloops that have formed in the chains and, unlike in the disk system, the voids can never be fully collapsed by repeated cycling.

The fact that the granular polymers do not exhibit the same behavior at the jamming transition as the bidisperse disk systems do at Point J provides additional evidence that jamming does not occur with universal features in all systems, and that the criticality found in the bidisperse disk systems may be associated with a special type of jamming. Additional studies on a variety of different types of systems would need to be performed to confirm whether the jamming behavior is indeed different for each system or whether there is a small number of different classes of jamming behaviors, with the granular polymer system and the bidisperse disk system falling into separate classes.

In summary, we have introduced a numerical model of 2D granular polymers that can be used to study the jamming transition. The onset of jamming occurs at a density that decreases with increasing chain length and saturates for long chain lengths. The decrease of the jamming density results from the formation of rigid semiloops in the granular chains which permit stable voids to exist in the packing, in excellent agreement with recent 3D experiments on granular polymers. For fixed chain length, the jamming density decreases when the chains are made stiffer since the rigid semiloops, and the voids stabilized by them, are larger. The jamming density can also be further decreased by increasing the fraction of granular loops present in the packing, which is also in agreement with experimental observations. The fact that our 2D simulations agree so well with the 3D experiments of Ref. [22] indicates that the formation of semiloops in the chains is essentially a 2D phenomenon. In comparison to bidisperse disk systems which show a nearly linear increase in the pressure as a function of density, characteristic of a critical phenomenon, in the granular polymer systems the pressure increases as a power law with exponent significantly larger than 1, suggesting that the jamming transition in the granular chain system is different in nature from jamming in the bidisperse disks and may be related to the type of jamming that occurs for frictional grains.

We thank R. Ecke and R. Behringer for useful comments. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]: A.J. Liu and S.R. Nagel, Nature (London) 396, 21 (1998).
[2]: C.S. O'Hern, L.E. Silbert, A.J. Liu, and S.R. Nagel, Phys. Rev. E 68, 011306 (2003).
[3]: F.A. Gilabert, J.-N. Roux, and A. Castellanos, Phys. Rev. E 75, 011303 (2007).
[4]: G. Lois, J. Blawzdziewicz, and C.S. O'Hern, Phys. Rev. Lett. 100, 028001 (2008).
[5]: M. Mailman, C.F. Schreck, C.S. O'Hern, and B. Chakraborty, Phys. Rev. Lett. 102, 255501 (2009).
[6]: A. Donev, R. Connelly, F.H. Stillinger, and S. Torquato, Phys. Rev. E 75, 051304 (2007).
[7]: C.S. O'Hern, S.A. Langer, A.J. Liu, and S.R. Nagel, Phys. Rev. Lett. 88, 075507 (2002).
[8]: S. Henkes and B. Chakraborty, Phys. Rev. Lett. 95, 198002 (2005).
[9]: T.S. Majmudar, M. Sperl, S. Luding, and R.P. Behringer, Phys. Rev. Lett. 98, 058001 (2007).
[10]: P. Olsson and S. Teitel, Phys. Rev. Lett. 99, 178001 (2007).
[11]: C. Heussinger and J.-L. Barrat, Phys. Rev. Lett. 102, 218303 (2009).
[12]: J.A. Drocco, M.B. Hastings, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. Lett. 95, 088001 (2005).
[13]: R. Candelier and O. Dauchot, Phys. Rev. Lett. 103, 128001 (2009).
[14]: A.R. Abate and D.J. Durian, Phys. Rev. E 76, 021306 (2007).
[15]: D.A. Head, Phys. Rev. Lett. 102, 138001 (2009).
[16]: Z. Zhang, N. Xu, D.T.N. Chen, P. Yunker, A.M. Alsayed, K.B. Aptowicz, P. Habdas, A.J. Liu, S.R. Nagel, and A.G. Yodh, Nature 459, 230 (2009).
[17]: E. Ben-Naim, Z.A. Daya, P. Vorobieff, and R.E. Ecke, Phys. Rev. Lett. 86, 1414 (2001).
[18]: J.J. Prentis and D.R. Sisan, Phys. Rev. E 65, 031306 (2002); K. Safford, Y. Kantor, M. Kardar, and A. Kudrolli, ibid. 79, 061304 (2009).
[19]: T. Sykes and T. Mullin, Phys. Rev. E 80, 051301 (2009).
[20]: N.Ch. Karayiannis and M. Laso, Phys. Rev. Lett. 100, 050602 (2008); N.Ch. Karayiannis, K. Foteinopoulou, and M. Laso, J. Chem. Phys. 130, 164908 (2009).
[21]: R.S. Hoy and C.S. O'Hern, Phys. Rev. Lett. 105, 068001 (2010).
[22]: L.-N Zou, X. Cheng, M.L. Rivers, H.M. Jaeger, and S.R. Nagel, Science 326, 408 (2009).
[23]: C.J. Olson Reichhardt and L.M. Lopatina, Science 326, 374 (2009).
[24]: P. Olsson and S. Teitel, Phys. Rev. E 83, 030302(R) (2011).
[25]: N.Ch. Karayiannis, K. Foteinopoulou, and M. Laso, Phys. Rev. E 80, 011307 (2009).
[26]: L.M. Lopatina, C.J. Olson Reichhardt, and C. Reichhardt, to be published.

File translated from T_EX by T_THgold, version 4.00.

Back to Home