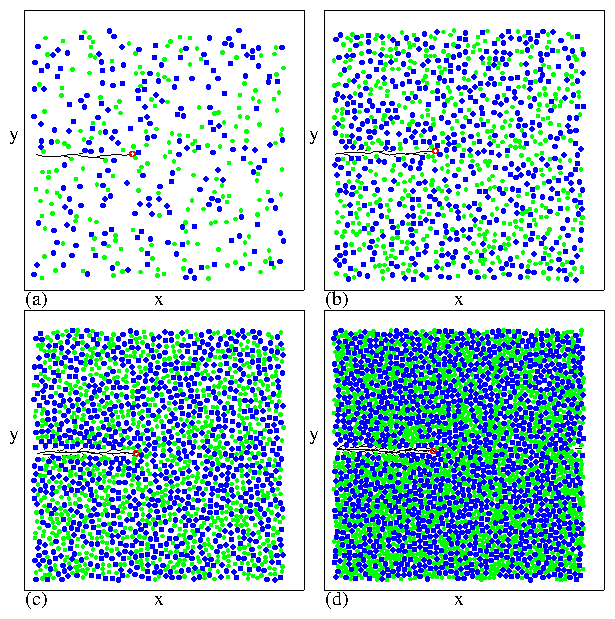
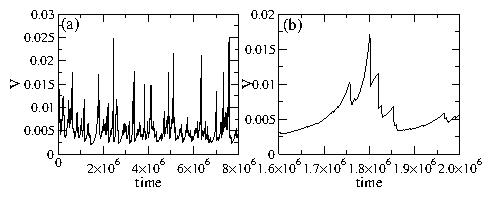
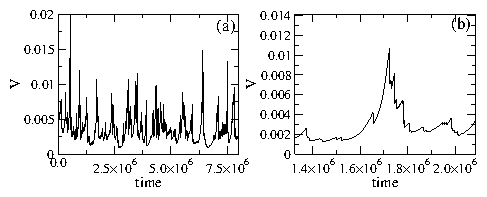
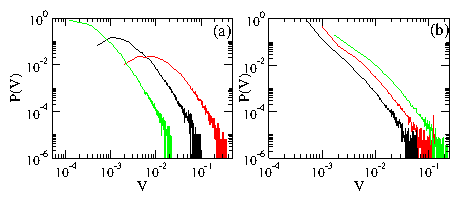
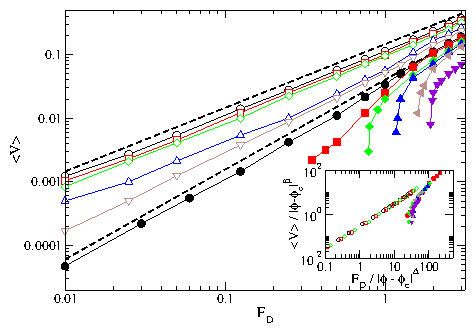
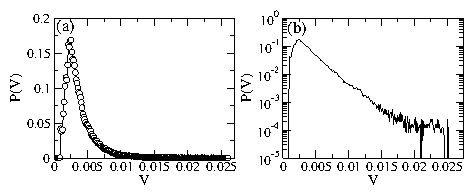 Figure 17:
(Color online)
〈V〉 vs FD on a log-log scale for
ϕ = 0.833 (open circles),
0.836 (open squares), 0.8386 (open diamonds), 0.8406 (open up triangles),
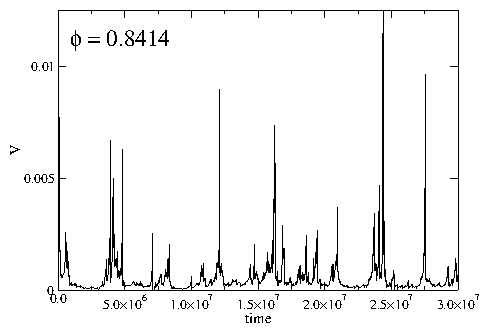
0.8414 (open down triangles),
0.8427 (filled circles), 0.8432 (filled squares), 0.8438 (filled diamonds),
0.844 (filled up triangles), 0.8453 (filled left triangles),
and 0.8464 (filled down triangles).
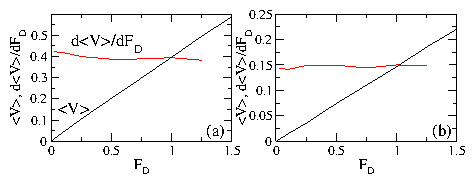
Upper dashed line: a linear fit showing that for
ϕ = 0.833, the velocity of the probe
increases linearly with the external drive.
Lower dotted line: a power law fit with an exponent of
1.41
for ϕ = 0.8427.
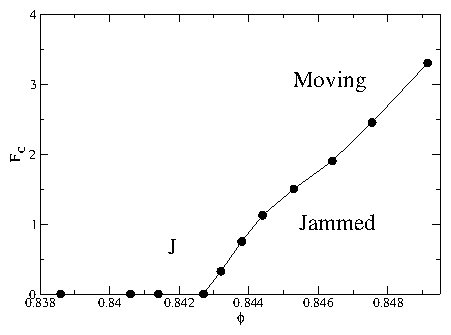
For ϕ > 0.8427 the probe particle
remains pinned for small but nonzero values of FD until
FD exceeds the critical force FC.
The value of FC increases with increasing ϕ for ϕ > 0.8427.
Inset: Scaling plot of 〈V〉/|ϕ−ϕc|β versus
FD/|ϕ−ϕc|∆ for the same data with β = 0.7 and
∆ = 0.496.
Figure 17:
(Color online)
〈V〉 vs FD on a log-log scale for
ϕ = 0.833 (open circles),
0.836 (open squares), 0.8386 (open diamonds), 0.8406 (open up triangles),
0.8414 (open down triangles),
0.8427 (filled circles), 0.8432 (filled squares), 0.8438 (filled diamonds),
0.844 (filled up triangles), 0.8453 (filled left triangles),
and 0.8464 (filled down triangles).
Upper dashed line: a linear fit showing that for
ϕ = 0.833, the velocity of the probe
increases linearly with the external drive.
Lower dotted line: a power law fit with an exponent of
1.41
for ϕ = 0.8427.
For ϕ > 0.8427 the probe particle
remains pinned for small but nonzero values of FD until
FD exceeds the critical force FC.
The value of FC increases with increasing ϕ for ϕ > 0.8427.
Inset: Scaling plot of 〈V〉/|ϕ−ϕc|β versus
FD/|ϕ−ϕc|∆ for the same data with β = 0.7 and
∆ = 0.496.
|