New Journal of Physics 20, 025002 (2018)

Avalanche Dynamics for Active Matter in Heterogeneous Media

C. J. O. Reichhardt and C. Reichhardt

Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

Keywords: active matter, avalanches, heterogeneous media
Received 18 September 2017
Revised 6 December 2017
Accepted for publication 21 December 2017
Published 7 February 2018

Abstract

Using numerical simulations, we examine the dynamics of run-and-tumble disks moving in a disordered array of fixed obstacles. As a function of increasing active disk density and activity, we find a transition from a completely clogged state to a continuous flowing phase, and in the large activity limit, we observe an intermittent state where the motion occurs in avalanches that are power law distributed in size with an exponent of β = 1.46. In contrast, in the thermal or low activity limit we find bursts of motion that are not broadly distributed in size. We argue that in the highly active regime, the system reaches a self-jamming state due to the activity-induced self-clustering, and that the intermittent dynamics is similar to that found in the yielding of amorphous solids. Our results show that activity is another route by which particulate systems can be tuned to a nonequilibrium critical state.
1. Introduction
2. Simulation
3. Results
4. Discussion
5. Summary
References


1.  Introduction

There are numerous examples of driven collectively interacting systems that exhibit avalanches or intermittent behavior when driven over quenched disorder, including vortices in type-II superconductors [1,2,3], magnetic domain walls [4,5], earthquake models [6,7], and colloidal depinning over rough landscapes [8]. At a critical driving force Fc, there is a depinning transition from a pinned to a sliding state. Motion often occurs in avalanches close to the depinning transition, and if depinning is associated with critical features such as diverging characteristic lengths and times, the avalanches and other fluctuating quantities will exhibit broad or power law distributions [5,7]. Scale-free avalanche dynamics often appear near yielding or unjamming transitions, such as in the intermittent motion of dislocations in crystalline solids [9,10,11] or the rearrangements of particles at yielding in amorphous materials [12,13,14,15]. For loose assemblies of particles such as grains or bubbles, the shear modulus becomes finite above a density ϕj when a jamming transition occurs [16,17], and it is known that in such systems, the dynamics become increasingly intermittent as the jamming point is approached, producing power law distributions in a variety of dynamic quantities [18,19,20,21,22,23].
In the driven systems described above, the dynamics arise from some form of externally applied driving or shear. In contrast, in active matter systems the particles are self-driven. Examples of active matter systems that have been attracting increasing attention include pedestrian flow, biological systems such as run-and-tumble bacteria, and self-propelled colloids [24,25]. The behavior of these systems can be captured by a simple model consisting of sterically interacting hard disks with a self-mobility represented either by driven diffusion or run-and-tumble dynamics. In two dimensions, a non-active, thermal assembly of hard disks forms a uniform density liquid at finite temperature, and if the disk density is large enough, a jammed or crystalline state emerges [17]. If the disks are self-propelled or active, for large enough activity a transition can occur from the uniform liquid state to a phase separated state in which a high density cluster that can be regarded as a solid is surrounded by a low density gas of disks, even when the overall density of the system is well below that at which non-active disks would jam or crystallize [26,27,28]. Self-clustering occurs when multiple active disks collide and continue to swim into each other, producing an active load-bearing contact in a system containing no tensile forces, and it has been observed in experiments using self-propelled colloids [29,30] and in simulations of disks obeying driven diffusive or run-and-tumble dynamics [28]. Previous numerical studies [31] of active run-and-tumble disks driven through a random array of fixed obstacles show that for fixed active disk density, the average drift mobility of the disks is a nonmonotonic function of the activity, initially increasing with increasing run length, but then passing through a maximum and decreasing at large run lengths, with the onset of self-clustering or self-jamming coinciding with the mobility reduction. For a fixed run length, the mobility decreases as the active disk density increases due to crowding effects.
In this work we examine the motion of active run-and-tumble disks driven through a random array of fixed obstacles as a function of obstacle density and activity for the system previously studied in Ref. [31]. We find that there is a critical amount of disorder and activity above which the motion becomes highly intermittent and takes the form of avalanches that are power law distributed in size, P(s) ∝ s−β, with an exponent of β = 1.46 ±0.1. For a constant obstacle density but decreasing activity, the motion becomes more continuous, the avalanche behavior is lost, and the disks act like a fluid moving through the obstacle array, while at zero or very small activity, the disks become completely clogged and there is no motion. We argue that in the limit of large activity, critical behavior occurs due to self-jamming or self-clustering, while in the low but finite activity limit the disks act like a liquid with continuous fluctuations. The critical behavior under an external drive can be viewed as analogous to a yielding transition of an amorphous solid close to a jamming point. We also find that for fixed active disk density, a critical amount of disorder in the form of obstacles must be added to produce power law distributed avalanche sizes, similar to the behavior observed for avalanches in certain magnetic systems [5,32,33]. From our results we identify three phases: a clogged phase with zero net drift, heterogeneous structure, and little motion; a flowing phase in which the disk velocity distribution is bimodal; and an intermittent phase in which the motion occurs in bursts or avalanches and the disk velocities are power law distributed. Our results indicate that activity can provide another method for tuning a system to a nonequilibrium critical state.
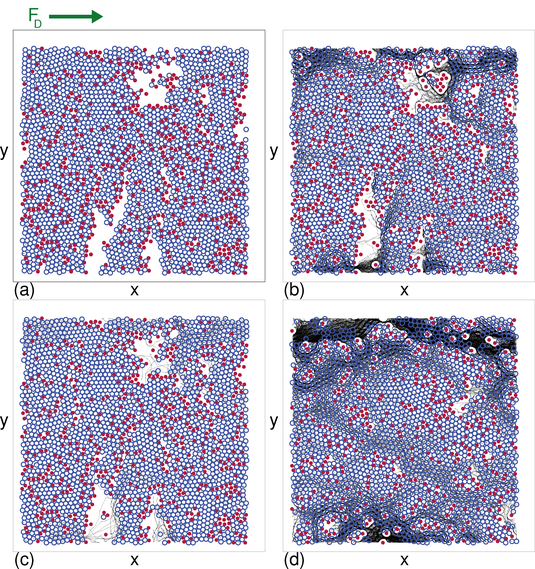
Fig1.png
Figure 1: The obstacle positions (red filled circles), which are fixed in space, active disks (dark blue open circles), and trajectories (light blue lines) for a system with ϕtot = 0.754. The driving force FD is applied in the x direction, as indicated by the arrow. (a) For low activity lr/d = 0.1 at ϕobs=0.1727, the disks become completely clogged and there is no motion. (b) For intermediate activity lr/d = 1 at ϕobs=0.1727, we find a combination of flowing and immobile active disks. (c) For high activity lr/d = 320 at ϕobs=0.1727, motion occurs only in bursts or avalanches. (d) A system with lr/d = 320 at a lower obstacle density of ϕobs = 0.1256.

2.  Simulation

We simulate a two-dimensional L ×L system with periodic boundary conditions in the x and y-directions containing Nobs obstacles and Na active disks of radius d/2=0.5. The size of the system is L/d=50. The active disks are allowed to move and the obstacle positions are permanently fixed, but otherwise the obstacles and active disks are identical. Steric disk-disk interactions are given by a harmonic repulsive force Fdd = k(rij−d)Θ(rij − d)∧rij where rij is the distance and ∧rij is the displacement vector between a pair of disks. The spring constant k = 100 is large enough that, for the parameters we consider, disks overlap by less than 0.005d, so the system is approximately in the hard disk limit. The obstacle area coverage is ϕobs = Nobsπd2/4L2, the active disk area coverage is ϕa = Naπd2/4L2, and the total area coverage is ϕtot = ϕobs + ϕa. In an obstacle-free system with ϕobs = 0, in the absence of activity the disks form a hexagonal solid near ϕa = 0.9. The active disk dynamics obey the following overdamped equation of motion:
η dri
dt
 = Fiinter + Fim + Fiobs + FD
(1)
where the damping coefficient η = 1. The interactions between active disks are given by Fiinter=∑jNaFddij, and Fim=Fm∧m is a run-and-tumble motor force with Fm=0.5 that acts in a randomly chosen running direction ∧m for a running time τδt, after which a new running direction ∧m′ is randomly chosen. Here τ is the dimensionless number of simulation time steps in the run and δt=0.002 is the size of the simulation time step. In the absence of any collisions, during the running time an active disk moves a run length lr = Fmτδt/η. The disks do not all tumble simultaneously; each disk has a clock that tracks the time until the next tumble, and these clocks are intialized to random values. The obstacle forces are given by Fobs=∑kNobsFddik, and the external driving force FD=FD∧x is applied uniformly to all active disks with FD=0.5. To initialize the system, we place a density ϕtot of disks at nonoverlapping locations in the sample, and then randomly choose Nobs of the disks to serve as obstacles, fixing them in their original random locations. We apply a driving force FD and wait several million simulation time steps to ensure that we have reached a steady state before measuring the active disk velocity fluctuations and displacements. We obtain a time series of the average active disk velocity in the driving direction, V(t) = Na−1∑Nai vix(t), where vix(t)=vi(t)·∧x, and also measure the time-averaged active disk velocity in the driving direction 〈V 〉 = 〈V(t)〉. We quantify the activity level using lr/d and the disorder using ϕobs. This system was previously studied in Ref. [31], where we showed that the average velocity decreases in the limit of large run lengths.

3.  Results

Fig2.png
Figure 2: Average active disk velocity 〈V〉 in the direction of the applied drive vs ϕobs for a system with ϕtot = 0.754 at lr/d = 1 (red squares) and lr/d = 320 (blue circles). The green arrow indicates the value of ϕobs used in Fig. 3. Inset: Data from the main panel plotted on a log-log scale.
In Fig. 1 we illustrate the behavior of a system with ϕtot = 0.754. For ϕobs = 0.1727, Fig. 1(a) shows that at a very low activity level of lr/d=0.1, the disks become completely clogged with 〈V〉 = 0. In Fig. 1(b) at a higher level of activity lr/d = 1, we find a coexistence of jammed and moving active disks, while for large activity lr/d=320 in Fig. 1(c), the flow is highly intermittent and occurs through avalanches. Figure 1(d) shows that in an lr/d=320 system with a lower obstacle density of ϕobs = 0.1256, the flow of active disks becomes continuous again.
Fig3.png
Figure 3: (a) A portion of the time series of the average disk velocity V(t) from the system in Fig. 2 at ϕtot = 0.754, ϕobs = 0.1727, and lr/d = 320, where the motion is strongly intermittent. (b) The avalanche size distribution P(s) from the complete time series for the system in panel (a). The dashed line is a power law fit with exponent β = 1.465 ±0.15. (c) V(t) for the lr/d=1 system from Fig. 2. (d) P(s) for the system in panel (c) has a bimodal rather than a power law shape.
In Fig. 2 we plot the average drift velocity per active disk in the direction of drive 〈V〉 versus ϕobs over the range 0 ≤ ϕobs ≤ 0.196 for a system with ϕtot = 0.754 at lr/d = 1 and lr/d=320. As shown in previous work [34], self clustering occurs when lr/d > 10 for ϕtot=0.754, so the values of lr/d in Fig. 2 are representative of the liquid state and the phase separated state. At ϕobs = 0 the disks undergo free flow drift giving 〈V〉 = FD/η = 0.5 for all lr/d; however, as ϕobs increases, 〈V〉 is always lower in the phase separated lr/d=320 sample than in the liquid lr/d=1 sample. For ϕobs > 0.15, the motion in the lr/d = 320 system becomes highly intermittent, as shown by the plot of V(t) in Fig. 3(a) for the system in Fig. 2 with lr/d=320 at ϕobs=0.1727, which is also illustrated in Fig. 1(c). Here the motion occurs in bursts or avalanches. In contrast, the lr/d=1 sample at the same obstacle density has a much more continuous V(t), as shown in Fig. 3(b) and illustrated in Fig. 1(b). The average velocity ratio 〈V〉lr=1/〈V〉lr=320=17 for ϕobs=0.1727, indicating how strongly an increase in activity can reduce the flow through the system. We use the time series V(t) to construct an avalanche size distribution P(s), where s is defined to be equal to the instantaneous value of V. In Fig. 3(b), P(s) for the lr/d=320 system can be fit to a power law distribution over two decades with an exponent β = 1.465±0.15, while in Fig. 3(d), P(s) for the lr/d=1 system is not broad but has a bimodal distribution, where the second peak is characteristic of the flow of a liquid through a disordered medium [8].
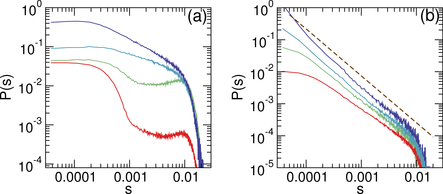
Fig4.png
Figure 4: Avalanche size distribution P(s) for a system with ϕtot = 0.754 and ϕobs = 0.1727. (a) lr/d = 0.3 (red), 1.0 (green), 10 (light blue), and 20 (dark blue), from bottom to top. The curves have been shifted vertically for clarity by factors of 1, 10, 20, and 40, respectively. (b) lr/d = 80 (red), 160 (green), 320 (light blue), and 640 (dark blue), from bottom to top. The curves have been shifted vertically for clarity by factors of 1, 3, 6, and 16, respectively. 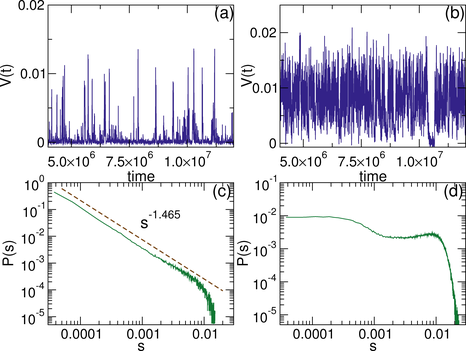The dashed line indicates a power law fit with exponent β = 1.465.
In Fig. 4(a) we plot P(s) for a system with ϕtot = 0.754 and ϕobs = 0.1727 at lr/d = 0.3, 1.0, 10, and 20. The bimodal characteristics of the lr/d = 0.3 and lr/d=1.0 distributions are lost for lr/d=10 when the system acts like a fluid. The avalanche size distribution broadens when self-induced clustering begins to occur, and for lr/d = 20 and above it is possible to fit a power law to a portion of P(s). Figure 4(b) shows P(s) for the same system at lr/d = 80, 160, 320, and 640 along with a dashed line indicating a power law fit with exponent β = 1.465. The region over which P(s) obeys a power law grows in extent as lr/d increases, and the exponent falls in the range 1.35 ≤ β ≤ 1.5. The overall shape of P(s) remains nearly the same for lr/d=80 and above, but the time intervals separating successive avalanche events increase with increasing lr/d. These results indicate that there is a critical lr/d above which scale-free avalanches occur, and that this critical value corresponds to the point at which the system begins to act like a solid rather than a liquid.
Fig5.png
Figure 5: The time-average disk flux through the system 〈V〉 vs lr/d for samples with ϕtot = 0.754 and ϕobs = 0.1727 showing the completely clogged regime at low lr/d, the flow regime at intermediate lr/d, and the intermittent or avalanche regime at large lr/d. (b) The fraction c of disks that are in the largest cluster vs lr/d for a system with ϕtot=0.754 and ϕobs=0, showing that the onset of the intermittent phase correlates with the onset of self-clustering.
In Fig. 5(a) we plot 〈V〉 versus lr/d for the system in Fig. 2 at ϕtot = 0.754 and ϕobs = 0.1727. Based on the behavior of the P(s) distributions, as illustrated in Fig. 4, we identify three regimes: a fully clogged state for lr/d ≤ 0.2, where 〈V〉 = 0 as illustrated in Fig. 1(a), a flowing or liquid like region for 0.2 < lr/d < 20, and an intermittent avalanche regime for lr/d ≥ 20. We measure the fraction c of disks that belong to the largest cluster using the cluster identification algorithm described in [35], and in Fig. 5(b) we plot c versus lr/d for an obstacle-free sample with the same ϕtot=0.754 as in Fig. 5(a) but with ϕobs=0, showing that the onset of the intermittent phase in the presence of obstacles correlates with an increase in self-clustering in the absence of obstacles. We define the intermittent phase to exist when c > 0.75 since this corresponds to the range of lr/d values for which the velocity distributions show a power law form, but there is no sharp transition into the intermittent phase.
The avalanche size distributions are also affected by the obstacle density. In Fig. 6(a) we plot P(s) for fixed ϕtot = 0.754 and lr/d = 320 at ϕobs = 0.1413, 0.157, and 0.1727. For ϕobs = 0.1413, even though the system can self-cluster there is enough room for the disk clusters to flow freely around the obstacles, giving a peak at a characteristic avalanche size s ≈ 0.03, while at ϕobs = 0.157, avalanches of size s > 0.2 are lost and P(s) begins to broaden. In Fig. 6(b) we plot P(s) for the same system with ϕobs = 0.1727, 0.1884, and 0.2. The maximum avalanche size smax continues to decrease as the obstacle density increases, and at ϕobs = 0.2041 the avalanche motion is completely suppressed since 〈V〉 = 0. This behavior is similar to what has been predicted for models of avalanches in magnetic systems, where it is necessary to add a critical amount of disorder in order to obtain avalanches that are power law distributed in size [5,32,33]. For weak disorder the magnetic avalanches are dominated by system spanning events, while for strong disorder only small avalanches occur.
Fig6.png
Figure 6: Avalanche size distributions P(s) for a system with ϕtot = 0.754 and lr/d = 320 at (a) ϕobs = 0.1413 (green), 0.157 (red) and 0.1727 (blue). (b) The same for ϕobs = 0.1727 (blue), 0.1884 (red), and 0.2 (green). The dashed lines are power law fits with β = 1.465.
Fig7.png
Figure 7: P(s) for a system with ϕobs = 0.1727 and lr/d = 320 at ϕtot = 0.377 (light blue), 0.5 (green), 0.628 (red), and 0.754 (dark blue). The dashed line is a power law fit with exponent β = 1.465.
In Fig. 7 we show P(s) for a system with fixed ϕobs = 0.1727 and lr/d = 320 at ϕtot = 0.377, 0.5, 0.628, and 0.754, along with a power law fit with exponent β = 1.465. For ϕtot = 0.377 and ϕtot=0.5, P(s) cannot be fit by a single power law, while for ϕtot = 0.65 and ϕtot=0.754, there is good agreement with the power law fit, indicating that critical behavior only appears when the system is not too sparse.

4.  Discussion

We consider the origin of the criticality we observe in our active matter system. When lr/d and ϕa are large enough, the obstacle-free system enters a phase separated state in which the dense cluster regions have a density close to the jamming density, so the dense regions can be viewed as an assembly of grains that is close to the critical Point J identified in Ref. [16]. Several studies of yielding in two-dimensional foams [36] and granular matter [37] identify avalanches that have a power law size distribution with an exponent of β = 1.5, while other simulations of yielding in two-dimensional granular matter give avalanches with a power law size distribution exponent of β = 1.43 [38]. The exponent we observe is close to the value β = 1.5 predicted using mean field models [39,40]. There are also studies of yielding in soft particulate matter systems in which an avalanche exponent of β = 1.35 appears [41], while experiments on frictional granular matter give an avalanche exponent of β = 1.24 [38]. We argue that in the thermal limit of small lr/d, our active disks behave like a liquid with short correlation lengths, so portions of the system can readily flow as long as there is space for motion between the obstacles. When lr/d=0 in the limit of zero activity, the disks reach a completely clogged state where no fluctuations and therefore no avalanches occur. At large lr/d, the disks self-cluster and locally behave like a granular solid just on the verge of jamming, where large correlation lengths emerge, but the fact that the disks are active and are always attempting to move prevents the system from become permanently trapped in a jammed state. Instead, occasional activity-induced unjamming events occur that have the appearance of avalanches. The motion of our active disks is impeded by the presence of obstacles; however, even in the absence of obstacles, the active clusters can undergo local rearrangements that can occur suddenly as an avalanche. In previous simulations of active disks without obstacles, local velocity fluctuations of a single driven probe disk were power law distributed with an exponent of β = 2.0 when the activity was large enough to permit self-clustering to occur, while in the low activity limit where the system acts like a uniform fluid, the velocity fluctuation distribution was exponential [34].
Fig8.png
Figure 8: Phase diagrams showing the clogged phase I (red), the flowing phase II (green), and the intermittent phase III (blue), as defined by the features in the velocity distributions. (a) Phases as a function of lr/d vs ϕobs at ϕtot=0.754. (b) Phases as a function of ϕobs vs ϕtot at lr/d = 320.
Based on our simulation results we can construct phase diagrams in which we label the clogged state with 〈V〉 = 0 as phase I, the finite velocity flowing state with bimodal or non-power law velocity distributions as phase II, and the intermittent state with power law distributed velocities as phase III. In Fig. 8(a) we plot the evolution of the phases as a function of lr/d versus ϕobs for a system with fixed ϕtot = 0.754. When ϕobs < 0.14, the flowing phase II extends all the way down to low obstacle densities, while for ϕobs > 0.19, the obstacles percolate and the disks are unable to flow, remaining in the clogged phase I for all lr/d. We find the intermittent phase III motion only for ϕobs > 0.14 and lr/d > 20. In Fig. 8(b) we plot the locations of the phases as a function of ϕobs versus ϕtot in a system with lr/d = 320. For ϕtot > 0.9, the disks are always clogged since monodisperse disks crystallize at ϕtot = 0.9. Between the clogged phase I and the flowing phase II we observe a band of the intermittent phase III.
We have performed simulations with varied system size L/d for samples with lr/d = 320, ϕobs = 0.754, and ϕobs = 0.1727, and find that the avalanche exponent β is not affected by the system size although the support of the velocity distribution function extends out to slightly larger values for larger L/d. The maximum possible velocity is limited by the size of the finite drift force. We note that in comparing samples with different run times, the average 〈V〉 decreases as lr/d increases and the average time interval between avalanches increases, so in order to obtain an equivalent number of avalanches, samples with larger lr/d must be run for longer times than samples with smaller lr/d. The avalanche exponents are not affected when the total simulation time is increased.
In this work we focus on the case where an applied drive is used to characterize the avalanche behavior; however, it would also be interesting to study a dense active disk assembly in the presence of attractive pinning sites instead of obstacles to determine whether avalanches can also occur in the absence of an external drift force. An active disk can pass through a pinning site by overcoming a threshold force, but an active disk can never pass through an obstacle and must move around it. Previous numerical simulations of active disks moving through obstacle arrays without an external bias have only explored the low density regime [42]. It would also be interesting to determine whether other active matter models such as flocking particles exhibit avalanche behavior in the presence of quenched disorder. Simulations have already shown nonmonotonic transport behavior in such systems [43] as well as disorder-induced transitions from flocking to non-flocking states [44], and there are now experimental realizations of flocking systems with quenched disorder [45] that could be used to explore this question.

5.  Summary

We have numerically examined the avalanche behavior of active matter composed of run-and-tumble disks driven through a random obstacle array. We measure avalanche sizes in terms of the average instantaneous velocity of the active disks. At low activity the system becomes trapped in a completely clogged state, while at intermediate levels of activity the disks act like a fluid that can flow continuously among the obstacles, producing a bimodal avalanche size distribution. At large run lengths, the disks undergo self-clustering and their motion becomes highly intermittent, taking the form of avalanches of correlated disk motion that have a power law size distribution with an exponent of β = 1.465. We argue that the intermittency results from self-clustering, which causes the system to act like a granular solid that is near the jamming point, and that the activity-induced avalanches are similar to the behavior observed in the yielding of marginally stable solids such as foams or granular packings, where avalanches with similar size distribution power law exponents appear. Finally, we find that when the density of obstacles is large enough, the avalanche size distribution is cut off at large sizes, suggesting that there is a critical disorder density that maximizes the critical nature of the avalanches. Our results indicate that activity provides another route for creating critical nonequilibrium states in particulate matter.

Acknowledgments

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
Olson C J, Reichhardt C and Nori F 1997 Superconducting vortex avalanches, voltage bursts, and vortex plastic flow: Effect of the microscopic pinning landscape on the macroscopic properties Phys. Rev. B 56 6175
[2]
Bassler K and Paczuski M 1998 Simple model of superconducting vortex avalanches Phys. Rev. Lett. 81 3761
[3]
Altshuler E 2004 Experiments in vortex avalanches Rev. Mod. Phys. 76 471
[4]
Zapperi S, Cizeau P, Durin G and Stanley H E 1998 Dynamics of a ferromagnetic domain wall: Avalanches, depinning transition, and the Barkhausen effect Phys. Rev. B 58 6353
[5]
Sethna J P, Dahmen K and Myers C R 2001 Crackling noise Nature 410 242
[6]
Carlson J M and Langer J S 1989 Properties of earthquakes generated by fault dynamics Phys. Rev. Lett. 62 2632
[7]
Fisher D S 1998 Collective transport in random media: From superconductors to earthquakes Phys. Rep. 301 113
[8]
Reichhardt C and Reichhardt C J O 2017 Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review Rep. Prog. Phys. 80 026501
[9]
Miguel M-C, Vespignani A, Zapperi S, Weiss J and Grasso J-R 2001 Intermittent dislocation flow in viscoplastic deformation Nature 410 667
[10]
Zaiser M 2006 Scale invariance in plastic flow of crystalline solids Adv. Phys. 55 185
[11]
McDermott D, Reichhardt C J O and Reichhardt C 2016 Avalanches, plasticity, and ordering in colloidal crystals under compression Phys. Rev. E 93 062607
[12]
Salerno K M, Maloney C E and Robbins M O 2012 Avalanches in strained amorphous solids: Does inertia destroy critical behavior? Phys. Rev. Lett. 109 105703
[13]
Lin Jie, Gueudre T, Rosso A and Wyart M 2015 Criticality in the approach to failure in amorphous solids Phys. Rev. Lett. 115 168001
[14]
Regev I, Weber J, Reichhardt C, Dahmen K A and Lookman T 2015 Reversibility and criticality in amorphous solids Nature Commun. 6 8805
[15]
Nicolas A, Ferrero E E, Martens K and Barrat J-L 2017 Deformation and flow of amorphous solids: a review of mesoscale elastoplastic models Preprint arXiv:1708.09194
[16]
Liu A J and Nagel S R 1998 Nonlinear dynamics: Jamming is not just cool any more Nature 396 21
[17]
Reichhardt C and Reichhardt C J O 2014 Aspects of jamming in two-dimensional athermal frictionless systems Soft Matter 10 2932
[18]
Drocco J A, Hastings M B, Reichhardt C J O and Reichhardt C 2005 Multiscaling at point J: Jamming is a critical phenomenon Phys. Rev. Lett. 95 088001
[19]
Candelier R and Dauchot O 2010 Journey of an intruder through the fluidization and jamming transitions of a dense granular media Phys. Rev. E 81 011304
[20]
Reichhardt C J O and Reichhardt C 2010 Fluctuations, jamming, and yielding for a driven probe particle in disordered disk assemblies Phys. Rev. E 82 051306
[21]
Arévalo R and Ciamarra M P 2014 Size and density avalanche scaling near jamming Soft Matter 10 2728
[22]
Woldhuis E, Chikkadi V, van Deen M S, Schall P and van Hecke M 2015 Fluctuations in flows near jamming Soft Matter 11 7024
[23]
Franz S and Spigler S 2017 Mean-field avalanches in jammed spheres Phys. Rev. E 95 022139
[24]
Ramaswamy S 2010 The mechanics and statistics of active matter Annu. Rev. Condens. Matter Phys. 1 323
[25]
Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G and Volpe G 2016 Active Brownian particles in complex and crowded environments Rev. Mod. Phys. 88 045006
[26]
Fily Y and Marchetti M C 2012 Athermal phase separation of self-propelled particles with no alignment Phys. Rev. Lett. 108 235702
[27]
Redner G S, Hagan M F and Baskaran A 2013 Structure and dynamics of a phase-separating active colloidal fluid Phys. Rev. Lett. 110 055701
[28]
Cates M A and Tailleur J 2015 Motility-induced phase separation Annu. Rev. Condens. Mat. Phys. 6 219
[29]
Palacci P, Sacanna S, Steinberg A P, Pine D J, and Chaikin P M 2013 Living crystals of light-activated colloidal surfers Science 339 936
[30]
Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C and Speck T 2013 Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles Phys. Rev. Lett. 110 238301
[31]
Reichhardt C and Reichhardt C J O 2014 Active matter transport and jamming on disordered landscapes Phys. Rev. E 90 012701
[32]
Perkovic O, Dahmen K and Sethna J P 1995 Avalanches, Barkhausen noise, and plain old criticality Phys. Rev. Lett. 75 4528
[33]
Chern G-W, Reichhardt C and Reichhardt C J O 2014 Avalanches and disorder-induced criticality in artificial spin ices New J. Phys 16 063051
[34]
Reichhardt C and Reichhardt C J O 2015 Active microrheology in active matter systems: Mobility, intermittency, and avalanches Phys. Rev. E 91 032313
[35]
Luding S and Herrmann H J 1999 Cluster growth in freely cooling granular media Chaos 9 673
[36]
Kabla A, Scheibert J and Debregeas G 2007 Quasistatic rheology of foams: II. Transition to shear banding J. Fluid Mech. 587 45
[37]
Hayman N W, Ducloue L, Foco K L and Daniels K E 2011 Granular controls on periodicity of stick-slip events: kinematics and force-chains in an experimental fault Pure Appl. Geophys. 168 2239
[38]
Barés J, Wang D, Wang D, Bertrand T, O'Hern C S and Behringer R P 2017 Local and global avalanches in a 2D sheared granular medium Preprint arXiv:1709.01012
[39]
Dahmen K, Ben-Zion Y and Uhl J T 2009 Micromechanical model for deformation in solids with universal predictions for stress strain curves and slip avalances Phys. Rev. Lett. 102 175501
[40]
Salje E K H and Dahmen K A 2014 Crackling noise in disordered materials Ann. Rev. Condens. Mat. Phys. 5 233
[41]
Lin J, Lerner E, Rosso A and Wyart M 2014 Scaling description of the yielding transition in soft amorphous solids at zero temperature Proc. Natl. Acad. Sci. (USA) 111 14382
[42]
Zeitz M, Wolff K and Stark H 2017 Active Brownian particles moving in a random Lorentz gas Eur. Phys. J.E 40 23
[43]
Chepizhko O, Altmann E G and Peruani F 2013 Optimal noise maximizes collective motion in heterogeneous media Phys. Rev. Lett. 110 238101
[44]
Quint D and Gopinathan A 2015 Topologically induced swarming phase transition on a 2D percolated lattice Phys. Biol. 12 046008
[45]
Morin A, Desreumaux N, Caussin J-B and Bartolo D 2017 Distortion and destruction of colloidal flocks in disordered environments Nature Phys. 13 63


File translated from TEX by TTHgold, version 4.00.
 Back to Home