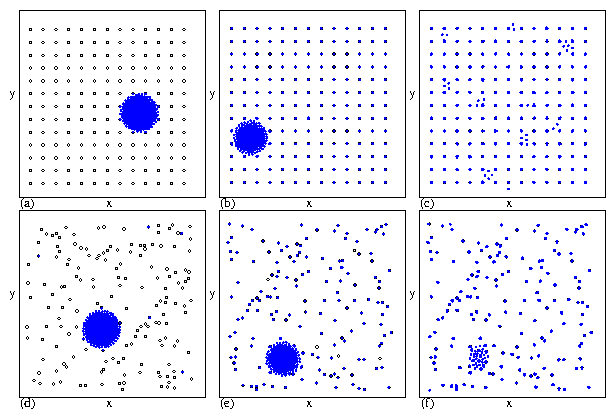
 Figure 3:
The vortex positions (filled circles) and pinning sites (open circles)
in snapshots of the moving state for a sample with (a-f) random pinning
and (g-i) periodic pinning
at Bϕ/B=0.64 under a
drive Fd=Fd∧x
showing the formation of heterogeneous
states at high drives.
(a) Fp = 0.3, Fd = 0.05 (i).
(b) Fp=0.3, Fd=0.8 (ii).
(c) Fp=0.7, Fd=0.25 (iii).
(d) Fp=0.7, Fd=3.0 (iv).
(e) Fp=1.3, Fd=2.5 (v).
(f) Fp=1.3, Fd=3.8 (vi).
(g) Fp = 0.7, Fd=1.6 (vii).
(h) Fp=1.3, Fd=0.96 (viii).
(i) Fp=1.3, Fd=3.0 (ix).
The labels i-vi [vii-ix]
correspond to the drives marked in figure 4(a-c) [(e,f)].
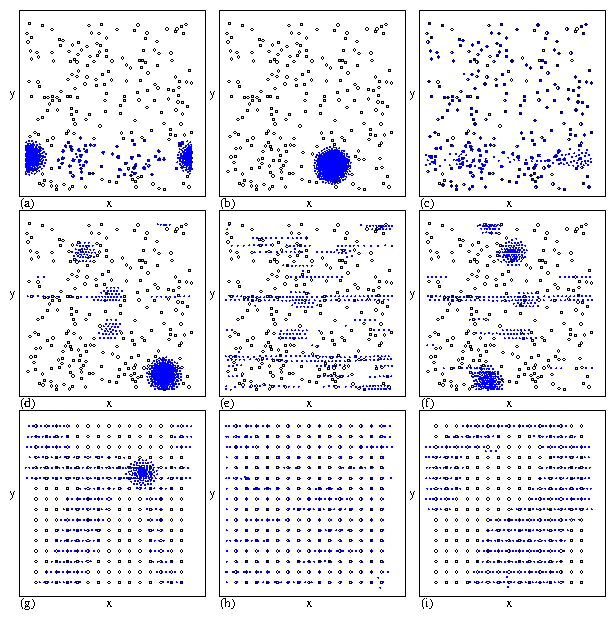
Figure 3:
The vortex positions (filled circles) and pinning sites (open circles)
in snapshots of the moving state for a sample with (a-f) random pinning
and (g-i) periodic pinning
at Bϕ/B=0.64 under a
drive Fd=Fd∧x
showing the formation of heterogeneous
states at high drives.
(a) Fp = 0.3, Fd = 0.05 (i).
(b) Fp=0.3, Fd=0.8 (ii).
(c) Fp=0.7, Fd=0.25 (iii).
(d) Fp=0.7, Fd=3.0 (iv).
(e) Fp=1.3, Fd=2.5 (v).
(f) Fp=1.3, Fd=3.8 (vi).
(g) Fp = 0.7, Fd=1.6 (vii).
(h) Fp=1.3, Fd=0.96 (viii).
(i) Fp=1.3, Fd=3.0 (ix).
The labels i-vi [vii-ix]
correspond to the drives marked in figure 4(a-c) [(e,f)].
|