Physical Review E 82, 041502 (2010)

Structural Transitions, Melting, and Intermediate Phases for Stripe- and Clump-Forming Systems

C. J. Olson Reichhardt, C. Reichhardt, and A.R. Bishop

Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 5 May 2010; revised manuscript received 31 August 2010; published 22 October 2010)

We numerically examine the properties of a two-dimensional system of particles which have competing long range repulsive and short range attractive interactions as a function of density and temperature. For increasing density, there are well defined transitions between a low density clump phase, an intermediate stripe phase, an anticlump phase, and a high density uniform phase. To characterize the transitions between these phases we propose several measures which take into account the different length scales in the system. For increasing temperature, we find an intermediate phase that is liquid-like on the short length scale of interparticle spacing but solid-like on the larger length scale of the clump, stripe, or anticlump pattern. This intermediate phase persists over the widest temperature range in the stripe phase when the local particle lattice within an individual stripe melts well below the temperature at which the entire stripe structure breaks down, and is characterized by intra-stripe diffusion of particles without inter-stripe diffusion. This is followed at higher temperatures by the onset of inter-stripe diffusion in an anisotropic diffusion phase, and then by breakup of the stripe structure. We identify the transitions between these regimes through diffusion, heat capacity, and energy fluctuation measurements, and find that within the intra-stripe liquid regime, the excess entropy goes into disordering the particle arrangements within the stripe rather than affecting the stripe structure itself. The clump and anticlump phases also show multiple temperature-induced diffusive regimes which are not as pronounced as those of the stripe phase.
I. SIMULATION
II. PHASES AS A FUNCTION OF DENSITY
A. Clump Phases
B. Stripe Phases
C. Anticlump and Uniform Phases
D. Phases and Neighbor Lengths
III. TEMPERATURE INDUCED DISORDER
A. Different Liquid Regimes in the Stripe Phase
B. Different Liquid Regimes Within the Clump and Anticlump Phases
IV. DISCUSSION
V. SUMMARY
References


There has been growing interest recently in understanding how collections of particles with competing interactions order or disorder under different conditions. A general understanding of such behaviors would have a profound impact on our ability to control self-organization and to tailor the functionality in systems of this class [1,2,3], such as collections of particles with completing interactions composed of a long-range repulsion and a short range attraction [4,5,6,7,8,9,15]. Specific systems where this type of interaction may be realized include charge ordering in cuprate superconductors [16,17,18,19], magnetic systems [20,21], bubble, stripe and clump phases in two-dimensional electron systems [22,23], and dense nuclear matter which forms pasta phases [24]. There are also a number of soft matter systems which can be effectively modeled as assemblies of particles with a finite range repulsive interaction that competes with a shorter range attractive interaction [25,26,27,28,29]. Recent simulations of colloidal systems with this type of interaction [25,26,28] generated many of the same types of phases observed in models with longer range repulsive interactions [9], indicating that many of the features found in systems with long range repulsion and short range attraction will be relevant for other systems with competing interactions as long the repulsive interaction is longer range than the attractive interaction. Clump, stripe, and bubble phases have also been shown to occur in systems where the particle-particle interactions are strictly repulsive provided that there are two length scales present in the repulsive interaction [2,3,10,11,12,13,14].
For systems with long-range repulsive interactions and short range attractive interactions, the onset of the different clump, stripe, and bubble phases can be controlled by directly varying the relative strength of the repulsive and attractive interactions at fixed density, or by holding the interactions fixed and varying the density of the system. In the clump phase where groups of particles form individual islands, the clumps organize into a crystal pattern at larger length scales due to the long range repulsive interaction between adjacent clumps [5,7,9,15]. Other phases include stripe or labyrinth structures and anticlump phases in which an ordered array of voids forms, along with a uniform phase that appears at very high densities. It is not known whether the transitions between the different phases are well defined, whether there are additional subphases, or what is the nature of the disordering or melting transitions of the phases in the presence of thermal fluctuations.
Our previous work on the long-range competing interaction system employed fixed density samples in which the relative attractive strength of the potential was varied [5]. We showed that for narrow regions of parameter space, the system forms a labyrinth or disordered stripe phase. Ordered stripes can be generated when the system is driven in the presence of quenched disorder; in this case, the stripes are aligned in the direction of the applied drive [5]. In the absence of quenched disorder, although the particles move under an applied uniform drive they do not experience the local shearing forces which are necessary to induce the plastic deformations required to align the stripe pattern. Simulations of a stripe-forming colloidal system with intermediate-range repulsive forces indicate that if a non-uniform drive is applied so as to create a shear in the system, then plastic deformation can arise and the stripes align in the direction of the shear [28]. In systems with multiple length-scale interactions, the inherent heterogeneity of the system may make it difficult to reach a completely ordered ground state and the system may adopt a metastable configuration. For example, if one patch of the system has a higher particle density than neighboring patches, it is difficult for an individual particle to escape from the overly dense patch due to the short range attractive forces, and it is also difficult for a particle to move into an underdense patch of the system due to the repulsive long range interactions [6,9]. Colloidal simulations with shorter range repulsive interactions also produced similar results and showed the formation of partially ordered states [25,26,28].
In this work we simulate the different types of states that arise as a function of particle density in a system with long range repulsive and short range attractive interactions. We introduce several new diagnostics to characterize these states and the transitions between them. We also examine how the states disorder as a function of temperature. The stripe states are particularly useful in understanding the thermal disordering process since diffusion along the stripes can be distinguished readily from diffusion between the stripes. We show that the stripe phase exhibits four temperature induced regimes, including a low temperature frozen phase, a phase where the particles diffuse along each stripe but where there is no particle transport between stripes, a regime where there is anisotropic diffusion but the stripe structure persists, and a high temperature phase where the stripe structure is destroyed. The onsets of these different phases produce signatures in the energy measures and energy fluctuations. We argue that since the stripe state can show an intra-stripe melting transition, the stripe structure may remain stable up to higher temperatures than the other possible structures, since the excess fluctuations in the stripe state can first melt the particles within each stripe rather than the stripe structure itself. We also show that similar melting behaviors occur in the clump and anticlump states.
Fig1.png
Figure 1: (Color online) V(R) (upper curve) and −dV(R)/dR (lower curve) for κ = 1 and B=2.

I.  SIMULATION

We consider a two-dimensional Langevin simulation of a system of size Lx ×Ly with periodic boundary conditions in the x and y-directions. In order to potentially accommodate a triangular lattice, we take Ly=L and Lx=1.097L. Within the system we place N interacting particles at a density ρ = N/(LxLy). In previous simulations we held the system size fixed and either varied the density by changing N or varied the relative strength of the attractive and repulsive particle interactions. Here we hold the particle-particle interaction strength fixed and fix N=380 but vary L in order to alter the density.
The dynamics of a single particle i obeys the following overdamped equation of motion:
η d Ri
dt
 = − N
∑
j ≠ i 
 ∇V(Rij) + FTi
(1)
where the damping coefficient η is set to 1. The particle-particle interaction has the following form:
V(Rij) = 1
Rij
 −Be−κ Rij
(2)
where Rij=|Ri−Rj| is the distance between particles located at Ri and Rj. The first term is a Coulomb repulsion, meaning that for very short distances the interaction is repulsive and the particles will not collapse to a point. The magnitude of the fluctuations experienced by the particles during the course of the simulation is such that Rij never drops below the minimum value Rij=0.1. Due to the long range nature of the Coulomb interaction, it is not possible to cut off the interaction range, so we use a Lekner real-space summation method to compute the long range term [30,31,32]. The net Coulomb energy associated with the charged particles is assumed to be compensated by a uniform jellium of opposite charge which does not alter the pairwise forces we use in our simulations. The second term is a short range attraction of Yukawa form with an inverse screening length of κ = 1.0 and with B=2.0. The value 1/κ serves as one of the characteristic length scales of the potential. A plot of V(R) and its derivative appears in Fig. 1. The last term in Eq. 1 is the random fluctuation force from finite temperature which has the following temporal correlations: 〈FT(t)〉 = 0 and 〈FTi(t)FjT(t′)〉 = 2ηkBTδijδ(t − t′). The initial particle positions are obtained using simulated annealing. In this process, the particles are placed at nonoverlapping positions in the sample and the temperature is set to a value well above the highest melting temperature exhibited by the sample. The temperature is then decreased in small increments and the system is held at each value of the temperature for an extended period of time. The temperature is decreased in these increments until zero temperature is reached.
Fig2.png
Figure 2: Particle locations in the entire sample after simulated annealing for different densities in the clump regime. The scale of the x and y axes changes in each panel. (a) ρ = 0.04, (b) ρ = 0.06, (c) ρ = 0.08, (d) ρ = 0.10, (e) ρ = 0.12, (f) ρ = 0.14, (g) ρ = 0.16, (h) ρ = 0.18, (i) ρ = 0.20, and (j) ρ = 0.22. The number of particles per clump increases as the density increases, as does the triangular ordering of the clump structure.

II.  PHASES AS A FUNCTION OF DENSITY

A.  Clump Phases

In Fig. 2(a-j) we plot the particle positions after simulated annealing in the low density regime ρ = 0.04 to ρ = 0.22 where the particles form a partially ordered to ordered triangular lattice of clumps. At the lowest density ρ = 0.04 in Fig. 2(a), a mixture of clumps appears where there are two to three particles in each clump along with a smaller number of individual particles. The number of particles per clump increases with increasing ρ so that at ρ = 0.10, for example, there are six particles per clump on average. The decrease in the number of particles per clump with decreasing density that we find at the lowest densities suggests that for even lower density than we have considered, the limit of only one particle per clump would occur and a triangular lattice would form. The system failed to form an ordered ground state at the lowest densities we considered even for a very slow simulated annealing procedure. This results from the very strong clumping tendency induced by the short range attraction combined with the relatively large inter-clump distances at these densities. Particles are strongly attracted into clumps, but the difference in energy at larger scales between having a clump with n particles or n+1 particles is too small to permit the particles that have already fallen into a clump to escape from the strong short-range attraction of the clump in order to form clumps of uniform size. The resulting polydispersity in clump size prevents the clumps from ordering into a larger-scale lattice.
Since the long-range Coulomb repulsion favors a triangular ordering of the clumps, the problem of trying to order a mixture of clumps of slightly different sizes has similarities to the filling of magnetic flux quanta at submatching fields on a triangular pinning array in a superconductor [33]. At matching fillings where the number of flux quanta is an integer multiple f of the number of holes, such as at f = 2, f=3, or f=n, with n integer, a triangular flux lattice forms; however, at non-integer fillings, most of the configurations are highly degenerate and disordered states appear, such as at f=n + 1/2. At other fields such as f=n/3, where an ordered tiling of the triangular lattice is possible, the ground state has several degenerate orientations, so any ordered state that forms is very likely to contain grain boundaries. Analogously, in our system a possible partial ordering could be expected for a low density filling where 1/3 of the clumps capture n + 1 particles and the remaining 2/3 of the clumps contain n particles. In superconducting network systems of the type considered in Ref. [33], the triangular ordering favored by the repulsive vortex-vortex interactions is strongly enhanced by the ordered substrate. In our system, the clumps move over a substrate-free continuum, which adds even more degeneracy to the system and makes it very difficult to observe ordered states. Even though there is a difference of only one or two particles in the number of particles in neighboring clumps, the polydispersity of clump sizes is largest at the lowest densities we consider, where the charge ratio between neighboring clumps can be as large as 1:2 or 1:3. It is known that large polydispersity in the particle interactions for two dimensional systems can lead to the formation of a disordered state [34].
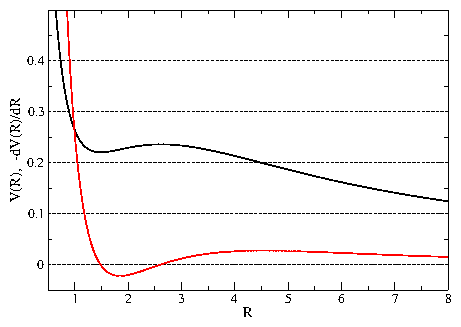
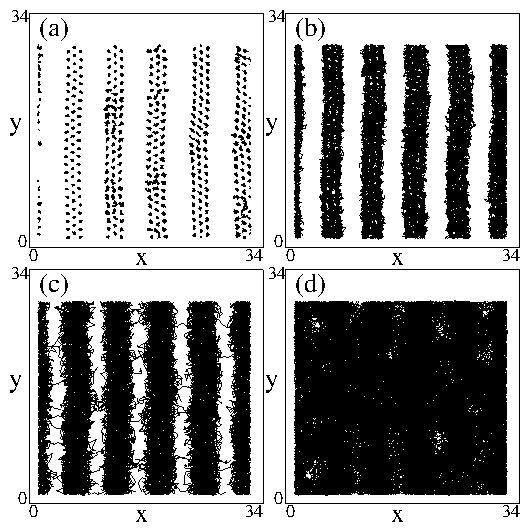
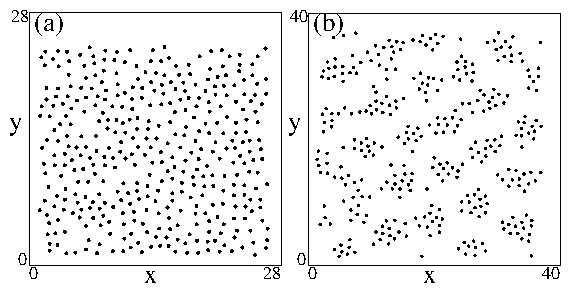
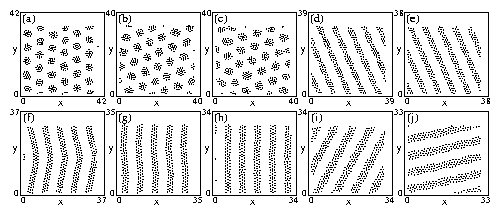
Fig3.png
Figure 3: Particle locations in the entire sample after simulated annealing for different densities in the clump and stripe regimes. The scale of the x and y axes is not fixed in all panels. (a) ρ = 0.24, (b) ρ = 0.26, (c) ρ = 0.27, (d) ρ = 0.28, (e) ρ = 0.30, (f) ρ = 0.32, (g) ρ = 0.34, (h) ρ = 0.36, (i) ρ = 0.38, and (j) ρ = 0.40. The clump phase appears for ρ < 0.28. For 0.20 ≤ ρ < 0.28, the clumps form a triangular lattice. For 0.28 ≤ ρ ≤ 0.44 a stripe phase occurs. The stripe structures have some density modulations along their length for ρ = 0.28 in panel (d) and ρ = 0.30 in panel (f), but are more uniform for the higher densities. The stripe phases at 0.32 ≤ ρ ≤ 0.36 in panels (f), (g), and (h) contain three rows of particles per stripe.
Fig4.png
Figure 4: Structure factor S(k) at densities (a) ρ = 0.26 in the clump state, (b) ρ = 0.36 in the stripe state, (c) ρ = 0.56 in the anticlump state, and (d) ρ = 0.6 in the uniform state.
At higher densities where the clumps contain larger numbers of particles, the difference in the number of particles in neighboring clumps is still only one or two particles. As a result, the effective polydispersity drops significantly and the system crosses over to a limit where each clump has close to the same charge. This tendency for the clumps to have increased triangular ordering as the clumps grow in size is clearly observable for ρ ≥ 0.2 in Fig. 2(i,j) and for 0.24 ≤ ρ ≤ 0.27 in Fig. 3(a-c). The triangular ordering also appears in the structure factor S(k) illustrated in Fig. 4. In Ref. [28], for colloidal systems with shorter range interactions, a larger polydispersity in the clump sizes appeared; however, the clumps formed an ordered triangular state whenever all of the clumps contained six or more particles. This ordering can be observed in the structure factor plots in Refs. [25,26]. In the short range, purely repulsively interacting soft-sphere system of Ref. [3], triangular ordering also appeared even for polydisperse clumps as long as the number of particles per clump was six or greater. Simulations of a mixed dimer and trimer clump state in a system with a two-step repulsive interaction produced disordered states very similar to the ones we observe [2]. These results indicate that clump states with small numbers of particles generally form partially disordered structures independent of the exact details of the particle-particle interaction potential, while clump states with larger numbers of particles per clump tend to form triangularly ordered structures.
Figures 2 and 3 indicate that the clump states form for ρ < 0.28. As the clusters grow in size with increasing density, we find that there is a tendency for clusters with certain "magic" numbers of particles to appear more often than clusters with non-magic particle numbers. In studies of isolated clusters of particles with the same interaction potential, the clusters with n = 14 particles were particularly stable [15]. A simple counting shows that clusters of size n=14 appear the most often at the highest clump densities of 0.24 ≤ ρ ≤ 0.27. The largest clusters of size n=16 occur at ρ = 0.27, while at ρ = 0.28 we observe the onset of stripe phases.

B.  Stripe Phases

In previous work on striped phases, the stripes formed disordered labyrinth patterns when a substrate of quenched disorder was present [5]. In the absence of quenched disorder, aligned stripes may form depending on the rate of thermal quenching. For rapid quench rates, different domains of stripe orientation can arise leading to a partially ordered stripe state; however, for sufficiently slow quench rates, the lower energy aligned stripe states can form. The orientation of the stripes is affected by the periodic boundary conditions and by the number of particles within each stripe. Our system is sufficiently small to permit formation of an ordered stripe state at the quench rates considered here. In systems of significantly larger size, stripe patterns that have no average net alignment would be expected to form.
Fig5.png
Figure 5: Particle positions in the entire sample after simulated annealing for different densities in the stripe and anticlump regimes. The scale of the x and y axes is nearly the same in all panels. (a) ρ = 0.42, (b) ρ = 0.44, (c) ρ = 0.46, (d) ρ = 0.47, (e) ρ = 0.48, (f) ρ = 0.50, (g) ρ = 0.52, (h) ρ = 0.54, (i) ρ = 0.56, and (j) ρ = 0.58. The stripe phase in panel (b) at ρ = 0.44 contains stripes that are close to four particles wide. The onset of the anticlump phases appears in panel (c) at ρ = 0.46. At the low density side of the anticlump phase, the structure is anisotropic, as can be seen by the thinning of the necks between anticlumps along the x direction in panel (c). For densities ρ > 0.46, the anticlump phase is no longer anisotropic.
At the lower-density end of the stripe regime, we observe stripes that are composed of three rows of particles which themselves form a sub-triangular lattice structure within the stripe, such as at ρ = 0.32 in Fig. 3(f). For densities ρ < 0.32, the particles within the stripes are partially disordered and form elongated quasi-clump states along the length of the stripe, creating pinch-like structures of the type seen in Fig. 3(d) and (e) at ρ = 0.28 and ρ = 0.30. For the higher densities of 0.32 ≤ ρ ≤ 0.34 in Figs. 3(f-g), each stripe is nearly consistently three particles wide. A representative plot of the structure factor S(k) in the stripe state appears in Fig. 4(b) for ρ = 0.36. As the density increases, bulges in the stripe that are four particles wide begin to form in a staggered pattern, as shown in Fig. 3(h,i) for ρ = 0.38 and ρ = 0.40. At ρ = 0.38 in Fig. 3(i), the stripes become partially disordered when a portion of the stripes buckle outward to form regions that are four particles wide. This process continues for ρ = 0.40 and ρ = 0.42 in Fig. 3(j) and Fig. 5(a). For ρ = 0.44, Fig. 5(b) shows that a large portion of the stripes are now four particles wide. Above ρ = 0.44, the system transitions into the anticlump phase of the type shown in Fig. 5(c). For different values of the screening length 1/κ than we consider here, other types of stripe phases containing only two rows or as many as five rows of particles could be realized; however, the general evolution of phases from clump to stripe to anticlump as a function of increasing density should hold for any choice of parameters.
Fig6.png
Figure 6: Particle positions in the entire sample after simulated annealing for different densities in the uniform regime where the ordering is mostly triangular. (a) ρ = 0.60, (b) ρ = 0.64, (c) ρ = 0.68, and (d) ρ = 0.72.

C.  Anticlump and Uniform Phases

Figure 5(c) shows the anticlump phase, composed of a triangular lattice of voids, which first forms at ρ = 0.46. At the low-density onset of the anticlump phase, the anticlump state is anisotropic and two of the six neck regions that surround each void are thinner than the other four, as seen in Fig. 5(c). The anticlump phases for 0.47 ≤ ρ ≤ 0.58, shown in Fig. 5(d-j), still have the triangular void ordering; however, the neck regions surrounding each void are now all of equal width so that the anisotropy found at ρ = 0.46 is absent. The particles outside of the voids attempt to form a triangular lattice segment that is roughly three particles wide. The structure factor S(k) for the anticlump state at ρ = 0.56 appears in Fig. 4(c). For ρ = 0.56 and 0.58, shown in Fig. 5(i) and Fig. 5(j), the width of the triangular lattice segments grows to be four particles wide before a transition to a slightly distorted uniform triangular lattice phase occurs at ρ = 0.6. The structure factor in this uniform phase is illustrated in Fig. 4(d) at ρ = 0.6. The triangular lattice uniform state persists for all ρ ≥ 0.6 and the triangular ordering improves with increasing density.
Fig7.png
Figure 7: (Color online) (a) Average distance to closest neighbor 〈dmin〉 vs ρ. The jumps indicate transitions between the clump, stripe, anticlump, and uniform phases. (b) The variation σn of the mean neighbor distance averaged over n neighbors for n = 3, 4, 5, and 6 (from bottom to top). The dotted lines indicate the locations of the transitions seen in panel (a). Compared to 〈dmin〉, two additional features appear in σn. There is a plateau in σn for 0.2 ≤ ρ ≤ 0.28 corresponding to the regime where the clumps form a triangular lattice, while for ρ < 0.2 the clumps are disordered. There is also a jump in σn at ρ = 0.38 which corresponds to the density at which the stripe state changes from having stripes that are three particles wide to having stripes that are four particles wide.

D.  Phases and Neighbor Lengths

To characterize the onset of the different phases, we compute the average closest neighbor distance 〈dmin〉 for the post-simulated annealing configuration at each density. To determine 〈dmin〉, we solve the all-nearest-neighbors problem with a simple algorithm. The distance from each particle i to its closest neighbor at Rnni is dmini=|Ri−Rnni|; then, 〈dmin〉 = N−1∑iN dmini. In Fig. 7(a) we plot 〈dmin〉 as a function of density ρ. For the lowest density clump phases, 〈dmin 〉 is large due to the presence of many individual particles whose closest neighbor is located in a different clump. As ρ increases, 〈dmin〉 decreases as the particles within each clump are compressed closer together. We can also use the value dmin to identify a characteristic energy scale Ec=1/dmin−B e−κdmin of the potential.
The transition to the stripe phase at ρ = 0.28 is marked by a sudden jump in 〈dmin〉 in Fig. 7(a). The stripes are able to pack the available space more efficiently than the clumps while maintaining a stripe-stripe spacing similar to the clump-clump spacing at the end of the clump phase. As a result, the particles within the stripes are able to decompress and shift to a larger average spacing as they form a partial triangular lattice within each stripe. The neighbor spacing 〈dmin〉 decreases with increasing ρ throughout the stripe phase as the particles within the stripe compress in order to maintain the stripe structure. The transition into the anticlump state at ρ = 0.46 is again accompanied by a sudden increase of 〈dmin〉 as the particles expand in order to take advantage of the additional area available to them in the anticlump structure. Within the anticlump phase, 〈dmin〉 decreases with increasing ρ as the particles are compressed into the diminishing space between the voids. The transition into the uniform phase appears as a large jump in 〈dmin〉 at ρ = 0.6. This jump is significantly larger than the other jumps in 〈dmin〉 since the particles are now able to fill the entire system evenly. As ρ continues to increase within the uniform phase, 〈dmin〉 decreases as the lattice constant of the triangular lattice shrinks. The sharp changes in 〈dmin〉 are associated with symmetry changes in the underlying lattice structure. In addition to computing the nearest neighbor distance dmin for each particle, we can determine the distance dinj, nj ∈ (1...nni) between a particle and each of its nni neighbors as identified by a Voronoi construction [35]. The distribution P(dinj) of dinj at a particular value of ρ is bidisperse for ρ < 0.6 due to the presence of two length scales: the short spacing between neighbors that are within the same clump, stripe, or on the same side of a void, and the longer spacing between neighbors that are in adjacent clumps or stripes or are on opposite sides of a void.
We compute the variation in particle spacing throughout the system at different values of ρ using a measure σn constructed in the following way: For each particle, we determine the mean distance dni from that particle to its n closest neighbors: dni=n−1∑dinj for nj ranging over the n closest neighbors only. We then determine the mean value μn of dn averaged over all particles, μn=N−1∑iNdni, and finally obtain the standard deviation σn of this quantity, σn=√{(N−1)−1∑iN(dni−μn)2}. In Fig. 5(b) we plot σn as a function of ρ for the number of closest neighbors n=3, 4, 5, and 6. At small values of ρ when the clumps contain only one or two particles, the measure σn performs poorly for n > 2, but for larger clumps and in all the remaining phases, the measure is well defined for n < 7. The dashed lines in Fig. 7(b) indicate the locations of the transitions found in Fig. 7(a). As n increases, the magnitude of the variance σn also increases for any given density ρ, which is expected since a larger number of neighbors are being averaged. Several of the features in σn correlate with the transitions found in 〈dmin〉 in Fig. 7(a); however, σn captures at least two features which do not appear clearly in Fig. 7(a). The first is that for n = 4, 5, and 6, σn rapidly decreases with increasing ρ up to ρ = 0.2 and then reaches a constant plateau which persists until the transition into the stripe state at ρ = 0.28. The onset of the plateau at ρ = 0.2 is correlated with the density at which the clumps start to form a more ordered triangular lattice, while for ρ < 0.2 the clump structure is much more disordered. This may indicate that the charge polydispersity effect described in Section II-A becomes small enough at ρ = 0.2 that a crossover to a more ordered triangular clump lattice can occur. The second distinctive feature is the increase in σn that occurs near ρ = 0.38 within the stripe regime. This feature is correlated with the density at which the stripes change from being an average of three particles wide to being an average of four particles wide. At the onset of the uniform phase at ρ = 0.6, σn drops and collapses so that all σn take the same value even for different choices of n. The σn measure indicates that in addition to the primary clump-stripe-anticlump phases, there can be sub-phases associated with changes in the average stripe width or the onset of ordering of the clumps.
Fig8.png
Figure 8: (Color online) The cumulative particle displacements dx (dark lower line) and dy (light upper line) vs time at different temperatures for the stripe sample at ρ = 0.36 in which the stripes are aligned along the y direction. (a) At T=0.031 both dx and dy are bounded. (b) At T=0.78, the increasing dy indicates that diffusion is occurring in the y-direction along the length of the stripes, but the flat dx indicates that there is no diffusion transverse to the stripes. (c) At T=2.0, the stripe structure is still present and the diffusion is anisotropic with dy > dx. There is now finite diffusion transverse to the stripes. (d) At T=2.53, the stripe structure is melted and the diffusion is isotropic.
Fig9.png
Figure 9: The particle positions (dots) and trajectories (lines) for a fixed period of time at different temperatures for the stripe phase at ρ = 0.36 highlighting the different diffusive regimes in Fig. 8. (a) At T=0.031, the particles in the stripe are frozen. (b) At T=0.78, the particles can diffuse along the stripes but there is no diffusion between stripes. (c) At T=2.0, the stripe structure is still present and motion occurs both along the stripes and across the stripes. It remains easier for the particles to diffuse along the stripes than across the stripes, producing an anisotropic diffusion signature. (d) At T=2.53, the stripe structure is destroyed and the particle motion is isotropic.

III.  TEMPERATURE INDUCED DISORDER

A.  Different Liquid Regimes in the Stripe Phase

We first consider melting transitions in the stripe state at ρ = 0.36, where the stripes are aligned in the y-direction as shown in Fig. 3(h). To examine the effect of temperature, we calculate the particle displacements dx and dy as a function of time for this phase at different temperatures for both the x and y directions.
dx,y(t) = (1/N) N
∑
i 
 |Rx,y(t) −Rx,y(t0)|.
(3)
In an isotropic liquid, we expect dx=dy. We consider the particle displacements defined above rather than a mean-squared displacement measure in order to distinguish different directions of particle motion. In Fig. 8 we plot dx and dy at temperatures T = 0.031, 0.78, 2.0, and 2.53. Figure 8(a) shows that at T=0.031 the displacements are bounded at long times and that dx and dy have approximately the same value. In Fig. 9(a), the particle trajectories during a fixed time at T=0.031 indicate that the particles undergo small displacements due to the thermal fluctuations but that both the stripe ordering and the crystalline ordering within the stripes are preserved, showing that the system is in a frozen state. We note that for much longer times than those plotted in Fig. 8(a), the values of dx,y do not increase but remain bounded at a nearly constant level. At T=0.78, plotted in Fig. 8(b), dy grows without bound while dx saturates and is bounded. Fig. 9(b) shows that for T=0.78 the particles readily diffuse along the stripes but there is no diffusion between the stripes. The fragmentary triangular particle ordering within the stripes is lost and an interesting state appears that acts like a liquid in one direction but like a solid in the other direction, which is characteristic of a smectic phase. For T=2.0, Fig. 8(c) indicates that both dy and dx increase with time; however, dy rises more rapidly indicating that the diffusion is anisotropic. In Fig. 9(c) the particle trajectories at T=2.0 show that there is a large amount of motion along the stripes accompanied by a smaller number of places where the particles have hopped from one stripe to the next. The overall stripe structure remains intact. For T=2.53, plotted in Fig. 8(d), dx and dy both increase at the same rate, indicating isotropic diffusion. Figure 9(d) shows that the stripe structure is destroyed at T=2.53 and the particle motion is uniform. Although the liquid state in Fig. 9(d) is isotropic, we observe short-lived clumps that do not occur in an isotropic liquid of purely repulsive particles [36].
Fig10.png
Figure 10: (Color online) The value of the cumulative particle displacements dx (open squares) and dy (filled circles) after 2×106 simulation time steps as a function of temperature T for the stripe system at ρ = 0.36. At low temperatures, there is a frozen regime with dx=dy; at intermediate temperatures, an anisotropic liquid appears with dy > dx; and at high temperatures an isotropic liquid forms with dx=dy.
To better characterize the onset of the different diffusive regimes we plot the value of dx and dy after 2×106 simulation time steps as a function of temperature T in Fig. 10. For T < 0.32, which is close to Ec for this density, the particles within the stripe remain frozen and the diffusion is isotropic. For 0.32 ≤ T ≤ 1.53, the particles can flow in a liquidlike fashion along the length of the stripes but there is no diffusion transverse to the stripes. Within this phase, if we measure dx,y for increasingly long times, the value of dy continues to increase but dx remains at a plateau value corresponding to the width of the stripe, which is the maximum distance the particles can diffuse in the x direction in this regime. For 1.53 < T ≤ 2.37, the stripe structure is still present although there is now some diffusion transverse to the stripes. The diffusion remains anisotropic with dy > dx. Finally for T > 2.37, the diffusion becomes isotropic when the stripe structure is destroyed.
Fig11.png
Figure 11: (a) The standard deviation of the energy σE vs T for the stripe phase at ρ = 0.36. The large peak at T=2.4 corresponds to the melting of the entire stripe structure. The smaller knee structure near T=0.5 corresponds to the onset of melting of the particles within the stripes. (b) The heat capacity C vs T for the same system shows a large peak at the stripe melting temperature and some features near the intra-stripe disordering transition.
Fig12.png
Figure 12: The particle positions at one instant in time for the stripe phase at ρ = 0.36. The scale of the x and y axes changes in each panel. (a) T=2.53 showing transient clump structures. (b) T=6.13 showing that the transient clumping is greatly reduced.
To further characterize the stripe melting, in Fig. 11(a) we plot σE, the standard deviation of the energy fluctuations, as a function of temperature. We obtain this measurement by collecting a time series of the total particle-particle interaction energy E during 5×106 simulation time steps while holding the system at a fixed temperature. We also compute the average energy ―E at each temperature and use this to construct the total heat capacity, C=d―E/dT, plotted in Fig. 11(b). Both the fluctuations σE and the heat capacity C show a pronounced peak at T=2.4 when the stripe structure melts into an isotropic liquid state. A knee structure appears in both measures near T=0.3 at the onset of the intra-stripe liquid phase. The magnitude of the energy fluctuations σE remains nearly constant for 0.3 < T < 1.4, inside the intra-stripe liquid. Both σE and C gradually decrease with increasing temperature above the stripe melting temperature. For purely repulsive particle assemblies, the magnitude of the energy fluctuations falls off very rapidly above the melting temperature. The heat capacity peak we find for our particles with competing long range repulsion resembles the specific heat peak found in Monte Carlo simulations of particles with competing finite range repulsion [25,26]. The slow decrease in σE for T > 2.4 in the liquid state for densities at which stripes form at low temperatures reflects the presence of short-lived clumps within the liquid which become smaller and even shorter-lived as T increases. In Fig. 12(a) we show a snapshot of the particle positions in the isotropic liquid phase at T=2.53, showing that the particle positions remain highly inhomogeneous on short time scales and form clump-like structures that change rapidly with time. For contrast, in Fig. 12(b) we show a similar snapshot deeper into the isotropic liquid phase at T=6.13, indicating that the transient clumping effect is significantly reduced at higher temperatures. In Fig. 11(b), C has the same trends as σE; however, the data is generally noisier.
An open question is whether the different regimes observed in the stripe state as a function of temperature are true phase transitions or only crossovers. The heat capacity data indicates that the melting transition into the fully isotropic liquid state is most likely a phase transition associated with a change in symmetry. Simulations of similar stripe and pattern forming systems generally find a transition from a stripe state to an isotropic state [2] which is associated in some cases with a dislocation unbinding transition [21]. Our system exhibits hysteresis in the transition to the stripe state; however, our simulation size is not large enough to rule out a dislocation-mediated transition in the stripe phase. The much weaker peak in C at the onset to the intra-stripe liquid phase suggests that the onset of this regime may be a crossover. We note that in most of our realizations of stripe phases, there are usually some topological defects present in the triangular ordering of the particles within the stripe. These defects may permit low energy particle motions that could obscure a true peak in the heat capacity at the onset of the intra-stripe liquid. In general, for a one-dimensional system there are no finite temperature phase transitions; however, in the stripe system, the ordering within the stripe is two-dimensional in nature and the particles in neighboring stripes are coupled to one another. Thus, a truly frozen state could occur in our quasi-one-dimensional stripes at finite temperature if the particles within the stripes were completely ordered. The onset of the anisotropic diffusive regime is most likely a crossover since individual particles within a stripe can be thermally activated out of the stripe. Due to the structure of the stripes, there should be a well-defined characteristic energy required for these hops to occur. When the temperature corresponding to this energy is reached, the inter-stripe diffusion rapidly increases.
Fig13.png
Figure 13: (Color online) The cumulative particle displacements D after 2×106 simulation time steps vs T for the clump phase at ρ = 0.26. The displacements increase rapidly once the clump structure is thermally destroyed. Unlike the stripe phase, the diffusion in the clump phase is isotropic. Also plotted is dD/dT vs T, showing a peak at the clump melting transition near T=2.0 along with a small rounded peak near T=0.25, which corresponds to the melting of the particles within each clump.

B.  Different Liquid Regimes Within the Clump and Anticlump Phases

We next consider the same set of measurements for the clump phase at ρ = 0.26. In Fig. 13 we plot D=dx=dy, the isotropic particle displacements after 2 ×106 simulation time steps, as a function of temperature in the clump phase. The diffusion is isotropic and Fig. 13 indicates that the displacements rapidly increase just below T = 2.0 with a cusp type feature appearing at T = 2.0. We also plot the derivative dD/dT, which passes through a peak just below T=2.0 at the point when the clumps begin to break apart. There is also a small feature in dD/dT near T=0.25 associated with the melting of the particles within each clump. If we perform the measurement over a longer period of time, the values of D for T < 1.125 remain unchanged while the values of D for T ≥ 1.125 increase.
Fig14.png
Figure 14: The particle positions (dots) and trajectories (lines) for a fixed period of time at different temperatures for the clump phase at ρ = 0.26. (a) At T=0.031 the clumps form a lattice and the particles within the clumps show little motion. (b) At T=0.78, the clumps still form a lattice but the particles are diffusing within each clump. (c) At T=1.28 the clump structure persists but interclump diffusion is now occurring in addition to intraclump diffusion. (d) At T=3.125 the clump lattice structure is destroyed and diffusion occurs freely throughout the system.
In Fig. 14(a) we illustrate the particle positions and trajectories in the clump state at ρ = 0.26 for T=0.031. Here the clump structure is ordered and the particles within each clump undergo little motion. At T=0.78, shown in Fig. 14(b), the clump structure is still present but the particles within each clump are highly disordered and diffuse rapidly within the clumps. This intra-clump liquid state has many similarities to the intermediate stripe liquid state. The overall structure of the system is ordered but subregions of the system are liquefied. In the stripe case, it was possible for the particles to diffuse along the full length of the stripes so that diffusion in this direction was unbounded. For the clump state, the diffusion in the intra-clump liquid always remains bounded by the finite clump size. In the stripe system the sharpness of the transition from the frozen stripe crystal to the intrastripe liquid is controlled by the amount of ordering within the stripe phase. In the clump system, a similar effect occurs. It was shown in previous work that there are certain magic sizes of individual clumps that produce highly ordered configurations of the particles within the clump [15]. For example, a clump containing 14 particles can form a stable segment of a triangular lattice which is free of internal topological defects. Additionally, studies of small numbers of particles in individual traps also indicate that the onset of rotational and translational disordering is affected by the number of particles in the trap and the degree of order in their arrangement [37,38,39,40]. For our clump system, this implies that if all the clumps had the same number of particles and each clump was also well ordered internally, such as for n=14 particles per clump, a well defined transition from a frozen clump phase to an intra-clump liquid phase should occur. In our system, not all the clumps have the same number of particles and some clumps contain particle numbers which produce less stable internal clump structures; therefore, our sample shows disorder at lower temperatures which smears out the transition to the intra-clump liquid.
In Fig. 14(c) we plot the particle trajectories at T=1.28 in the clump state. The clump structures persist and the particles within each clump have liquefied; however, there is now some diffusion of particles from clump to clump. This phase is similar to the stripe phase which showed anisotropic diffusion. In the clump system, the diffusion always remains isotropic. If we follow the trajectory of a single particle, we observe that it remains trapped within a single clump for a period of time, diffusing within that clump, before escaping from the clump and undergoing much more rapid diffusion until it is trapped by another clump. This type of motion resembles the caging dynamics seen in certain glassy systems where particles can locally diffuse in some region with an occasional long hop to another region where the particle again undergoes localized diffusion. At very short times, the behavior appears purely diffusive when the particles have not had enough time to experience the confining boundaries of the clump. At intermediate times, the behavior is subdiffusive due to the clump confinement, while at very long times, the behavior is diffusive since clump-clump diffusion can occur at this temperature. A similar behavior occurs for the stripe phases for diffusion in the direction perpendicular to the stripes. This behavior suggests it could be possible for these regions to exhibit glassy behavior, a topic which we will explore in a separate work.
In Fig. 14(d) for T=3.125, the clump lattice is destroyed and the system enters an isotropic liquid state. Just as in the stripe case, the liquid phase at temperatures not too far above the clump melting region shows short-lived density inhomogeneities which decrease in size and lifetime as the temperature increases.
Fig15.png
Figure 15: (a) The standard deviation of the energy σE vs T for the clump phase at ρ = 0.26. There is a peak at T=2.0 at the clump melting transition. (b) The heat capacity C vs T for the same system shows a similar peak at the clump melting temperature. In contrast to the stripe phase, there is no discernible feature in either quantity at the intra-clump melting transition.
In Fig. 15(a) we plot σE versus T for the clump state at ρ = 0.26 and in Fig. 14(b) we plot the corresponding heat capacity C vs T. Both quantities show a peak at T=2.0 where the clump structure breaks apart, followed by a slow decay at higher temperatures in the isotropic liquid regime. Neither quantity shows any noticeable features at the frozen clump solid to intra-clump liquid melting which is likely due to the fact that the clumps contain unequal numbers of particles.
Fig16.png
Figure 16: The cumulative particle displacements D after 2 ×106 simulation time steps vs T for the anticlump phase at ρ = 0.54. Here the onset of diffusion occurs at T=0.28 corresponding to the disordering of the particles within the non-void regions. This is followed by a second change in the behavior of D at T = 2.0, which corresponds to the melting or destruction of the void lattice.
Fig17.png
Figure 17: The standard deviation of the energy σE vs T for the anticlump phase at ρ = 0.54. There is a peak at T = 2.0 where the void lattice melts. There is also some indication of a change of slope near T=0.28. (b) The heat capacity C vs T for the same system shows a similar peak at T = 2.0. The heat capacity falls off much more rapidly above the melting transition than in the clump or stripe phases due to the fact that the isotropic liquid for the anticlump phase does not possess the same type of density inhomogeneities found for the clump and stripe phases.
We next examine the effect of temperature on the anticlump phase at ρ = 0.54. In Fig. 16(a) we show the cumulative displacements D=dx=dy after 2×106 time steps versus T. The displacements are isotropic and show a significant increase near T=0.28 followed by a smaller change near T = 2.0. The triangular void crystal remains intact up to T = 2.0, but diffusion through the entire sample begins at significantly lower temperatures. In Fig. 17(a) we plot σE for the anticlump phase at ρ = 0.54. There is a very sharp peak centered at T = 2.0 corresponding to the melting transition of the voids. There also is some indication of a change in slope near T=0.28. In Fig. 17(b) we show the corresponding heat capacity C versus T. There is a peak in C at T = 2.0 but there is no particular feature at T=0.28. The heat capacity falls off rapidly for T=2.0 due to the fact that the liquid phase does not exhibit the same large short-lived density inhomogeneities found above melting in the stripe and clump phases.
Fig18.png
Figure 18: The particle positions (dots) and trajectories (lines) for a fixed period of time at different temperatures for the anticlump phase at ρ = 0.54. (a) At T=0.125 the particles undergo little motion and the state is frozen. (b) At T=0.72 the void lattice persists but the particles have liquefied and diffuse throughout the non-void region. (c) At T=1.71 the behavior is similar to that for T=0.72 but with even more motion in the non-void regions. (d) At T=2.42 the void lattice is completely destroyed and diffusion occurs throughout the sample.
In Fig. 18 we illustrate the particle trajectories at different temperatures in the anti-clump phase at ρ = 0.54. At T=0.125, shown in Fig. 18(a), the particles undergo little motion indicating that the system is frozen. In Fig. 18(b) at T=0.72, the triangular void structure remains present but there is now particle motion through the non-void regions, indicating that particles are able to diffuse through the entire system. In Fig. 18(c) at T=1.71, the void structure persists but some particles can now move into the voids for short periods of time. The behavior for 0.28 < T < 2.0 has the same features found in the intermediate liquid phase for the stripe state where the individual particles have liquefied but the overall structure of the state remains solid. In Fig. 18(d) at T=2.42, the void structure has melted and diffusion can occur anywhere in the system.
Fig19.png
Figure 19: The particle positions at one instant in time at T=2.42. (a) The anticlump phase at ρ = 0.54. (b) The clump phase at ρ = 0.26
In Fig. 19(a) we plot the instantaneous particle positions in the anticlump phase for ρ = 0.54 at T=2.42 and in Fig. 19(b) we show the corresponding particle positions at the same temperature in the clump phase at ρ = 0.26. Just as in the stripe phase, the clump phase shows strong density inhomogeneities in the liquid state that decrease in size and lifetime with increasing temperature. In the anticlump phase, the liquid state found above melting is much more homogeneous and as a result the fluctuations in the energy are much smaller for the anticlump system above melting than for the stripe or clump phases. We also find a uniform density liquid for the higher density uniform regime above its melting temperature (not shown).
These results indicate that the clump, stripe, and anticlump phase all exhibit an intermediate fluid phase, where the internal ordering of individual particles is lost and selective diffusion can occur while the overall structure of the clump, stripe, or anticlump pattern remains intact.

IV.  DISCUSSION

One of our main findings is that the competing long-range repulsive and short-range attractive interactions produce a system that can exhibit both solid and liquid behavior simultaneously. The liquid-like behavior occurs on the short length scale of the spacing between individual particles. Motion on this small length scale initiates at temperatures well below the temperature at which the large scale patterns formed by the particles break apart. Future studies of the impact of the coexisting liquid and solid behavior could include determining how the existence of the two length scales affects measurable time scales. For example, the short-scale liquid could be probed with short-time measurements while the larger-scale solid state could be accessed using longer time measurements. The liquid-like nature of the system on short length scales might also play a role in permitting the system to adapt itself easily to a substrate or to an applied external field. For example, the ordering of a large length scale might be disrupted by quenched disorder in a system that had no short length scale degrees of freedom, whereas in our competing interaction system, the effect of the disorder could be compensated on the short length scale, permitting the large length scale ordering to be maintained intact. In essence, the existence of the short length scale degrees of freedom permits a screening of the disorder on the larger length scale. It would also be interesting to see which of the phases we observe, such as clump, stripe, or anticlump, is more adaptable to quenched disorder in this sense. Our system may have interesting connections to other types of disordered systems which exhibit liquid-like behaviors on some length and time scales but solid-like behaviors on other length and time scales. For example, glassy systems have properties that are in some sense inverted from what we observe, since glasses have liquid-like behavior on long length and time scales but solid-like behavior on short time and length scales. The time and length scale separation produced by competing interactions has clear potential for controlling novel functionality in materials, particularly those materials which contain additional degrees of freedom such as electronic, magnetic, superconducting, optical, biological, and so forth. The competing interactions can achieve a low-dimensional confinement of active regions, such as our short length scale liquid, embedded in a self-consistent supporting matrix, such as our larger length scale solid.

V.  SUMMARY

In summary, we have analyzed the different types of phases that can occur in a two-dimensional system with a competing long-range repulsion and a short range attraction as a function of density and temperature. At zero temperature and low densities, the system forms a clump phase. The particles cluster together in clumps and, due to the long range repulsion, the clumps move as far apart from each other as possible and attempt to form a macroscopic triangular lattice. When there are few particles in each clump, the overall structure of the clump lattice is disordered due to the large charge polydispersity of the small clumps. As the number of particles in each clump increases, this polydispersity effect is reduced and a triangular clump lattice appears. In addition to the triangular ordering of the clumps, there is also a tendency for the particles within each clump to form ordered or partially ordered structures. For higher densities, there is a sharp transition into a stripe state. The particles within each stripe tend to have triangular or partial triangular ordering. At still higher densities, a transition into an anticlump phase containing a triangular lattice of voids occurs, and at even higher densities there is a transition into a uniform phase with partial triangular ordering. We introduced several new measures to characterize the onset of the different phases as a function of density, including the calculation of the average distance to the closest neighbor.
As a function of increasing temperature, we find that the stripe phase exhibits clear multiple-step melting. A frozen phase with little or no diffusion occurs at low temperature. With increasing temperature the system melts into an intra-stripe liquid, where particles diffuse along the length of the stripes but do not diffuse between stripes and the overall stripe ordering remains intact. At higher temperatures, there is an onset of stripe-to-stripe particle motion leading to anisotropic diffusion, and the stripe structure continues to persist. Finally, there is a transition to an isotropic liquid where the stripe structure is destroyed and the diffusion becomes isotropic. The onset of these different regimes produces signatures in the heat capacity and in the energy fluctuations. We argue that the existence of an intermediate intra-stripe liquid indicates that excess entropy can be put into the motion of particles along the stripes rather than into destruction of the overall stripe structure. The presence of excess entropy is manifested as features in the energy fluctuations. We show that the clump and anticlump phases exhibit similar intermediate liquid regimes. In the clump phase, the particles remain confined within the clumps but are liquidlike and mobile inside the clumps, while the clump lattice remains solid. For the anticlump phase, the particles diffuse throughout the entire lattice while the void structure remains crystalline.
This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
M. Seul and D. Andelman, Science 267, 476 (1995).
[2]
G. Malescio and G. Pellicane, Nature Mater. 2, 97 (2003); Phys. Rev. E 70, 021202 (2004).
[3]
M.A. Glaser, G.M. Grason, R.D. Kamien, A. Kosmrlj, C.D. Santangelo, and P. Ziherl, EPL 78, 46004 (2007).
[4]
B.P. Stojkovic, Z.G. Yu, A.L. Cherynshev, A.R. Bishop, A.H. Castro Neto, and N. Grønbech-Jensen, Phys. Rev. B 62, 4353 (2000).
[5]
C. Reichhardt, C.J. Olson, I. Martin, and A.R. Bishop, Europhys. Lett. 61, 221 (2003); C. Reichhardt, C.J. Olson Reichhardt, I. Martin, and A.R. Bishop, Phys. Rev. Lett. 90, 026401 (2003).
[6]
C.J. Olson Reichhardt, C. Reichhardt, and A.R. Bishop, Phys. Rev. Lett. 92, 016801 (2004).
[7]
K. Nelissen, B. Partoens, and F.M. Peeters, Phys. Rev. E 71, 066204 (2005); F.F. Munarin, K. Nelissen, W.P. Ferreira, G.A. Farias, and F.M. Peeters, Phys. Rev. E 77, 031608 (2008).
[8]
Y.H. Liu, L.Y. Chew, and M.Y. Yu, Phys. Rev. E 78, 066405 (2008).
[9]
C.J. Olson Reichhardt, C. Reichhardt, I. Martin, and A.R. Bishop, Physica D 193, 303 (2004).
[10]
E. Jagla, J. Chem. Phys. 110, 451 (1999).
[11]
P.J. Camp, Phys. Rev. E 68, 061506 (2003); 71, 031507 (2005).
[12]
J. Fornleitner and G. Kahl, EPL 82, 18001 (2008).
[13]
A. Perera, Mol. Phys. 107, 487 (2009).
[14]
J. Fornleitner and G. Kahl, J. Phys.: Condens. Matter 22, 104118 (2010).
[15]
C.J. Olson Reichhardt, C. Reichhardt, and A.R. Bishop, Eur. Phys. J. E 22, 11 (2007).
[16]
J.C. Phillips, A. Saxena, and A.R. Bishop, Rep. Prog. Phys. 66, 2111 (2003).
[17]
D. Valdez-Balderas and D. Stroud, Phys. Rev. B 72, 214501 (2005).
[18]
T. Mertelj, V.V. Kabanov, and D. Mihailovic, Phys. Rev. Lett. 94, 147003 (2005).
[19]
V. Derzhko, J. Jedrzejewski, and T. Krokhmalskii, Eur. Phys. J. B 68, 501 (2009).
[20]
M. Seul and R. Wolfe, Phys. Rev. A 46, 7519 (1992).
[21]
A.D. Stoycheva and S.J. Singer, Phys. Rev. E 65, 036706 (2002).
[22]
M.M. Fogler, A.A. Koulakov, and B.I. Shklovskii, Phys. Rev. B 54, 1853 (1996); R. Moessner and J.T. Chalker, Phys. Rev. B 54, 5006 (1996); E. Fradkin and S.A. Kivelson, Phys. Rev. B 59, 8065 (1999).
[23]
M.P. Lilly, K.B. Cooper, J.P. Eisenstein, L.N. Pfeiffer, and K.W. West, Phys. Rev. Lett. 82, 394 (1999).
[24]
D.G. Ravenhall, C.J. Pethick, and J.R. Wilson, Phys. Rev. Lett. 50, 2066 (1983); G. Watanabe, T. Maruyama, K. Sato, K. Yasuoka, and T. Ebisuzaki, Phys. Rev. Lett. 94, 031101 (2005).
[25]
A. Imperio and L. Reatto, J. Phys.: Condens. Matter 16, S3769 (2004).
[26]
A. Imperio and L. Reatto, J. Chem. Phys. 124, 164712 (2006).
[27]
N. Osterman, D. Babic, I. Poberaj, J. Dobnikar, and P. Ziherl, Phys. Rev. Lett. 99, 248301 (2007).
[28]
A. Imperio, L. Reatto and S. Zapperi, Phys. Rev. E 78, 021402 (2008).
[29]
M. Golosovsky, Y. Saado, and D. Davidov, Phys. Rev. E 65, 061405 (2002); A. Imperio and L. Reatto, J. Chem. Phys. 124, 164712 (2006).
[30]
J. Lekner, Physica A 176, 485 (1991).
[31]
N. Grønbech-Jensen, Int. J. Mod. Phys. C 8, 1287 (1997).
[32]
M. Mazars, Mol. Phys. 103, 1241 (2005).
[33]
C. Reichhardt and N. Grønbech-Jensen, Phys. Rev. B 63, 054510 (2001).
[34]
M.R. Sadr-Lahijany, P. Ray, and H.E. Stanley, Phys. Rev. Lett. 79, 3206 (1997).
[35]
S.J. Fortune, Algorithmica 2, 153 (1987).
[36]
Y.-J. Lai and L. I, Phys. Rev. Lett. 89, 155002 (2002); R.A. Quinn and J. Goree, Phys. Rev. E 64, 051404 (2001); C. Reichhardt and C.J. Olson Reichhardt, Phys. Rev. Lett. 90, 095504 (2003).
[37]
W.-T. Juan, Z.-H. Huang, J.-W. Hsu, Y.-J. Lai, and L. I, Phys. Rev. E 58, R6947 (1998).
[38]
J.A. Drocco, C.J. Olson Reichhardt, C. Reichhardt, and B. Jankó, Phys. Rev. E 68, 060401(R) (2003).
[39]
R. Bubeck, C. Bechinger, S. Neser, and P. Leiderer, Phys. Rev. Lett. 82, 3364 (1999).
[40]
I.V. Schweigert, V.A. Schweigert, and F.M. Peeters, Phys. Rev. Lett. 84, 4381 (2000); W.P. Ferreira, B. Partoens, F.M. Peeters, and G.A. Farias, Phys. Rev. E 71, 021501 (2005).


File translated from TEX by TTHgold, version 4.00.

Back to Home