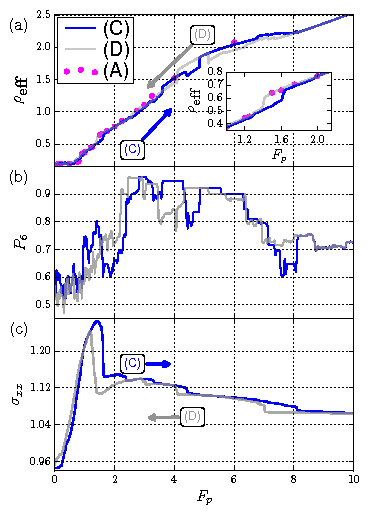
Fig. 1:
(a-u)
Particle positions at increasing substrate strength Fp
from left to right.
Top row (a-g): compression (C);
middle row (h-n): decompression (D);
bottom row (o-u): annealed with fixed confining force (A).
The confining forces Fp are:
0.1 (a,h,o), 0.5 (b,i,p), 1.14 (c,j,q),
1.39 (d,k,r), 1.62 (e,l,s), 2.23 (f,m,t), and 4.0 (g,n,u).
The ESI+
fully illustrate the
dynamics
of compression
and decompression.
Fig. 1:
(a-u)
Particle positions at increasing substrate strength Fp
from left to right.
Top row (a-g): compression (C);
middle row (h-n): decompression (D);
bottom row (o-u): annealed with fixed confining force (A).
The confining forces Fp are:
0.1 (a,h,o), 0.5 (b,i,p), 1.14 (c,j,q),
1.39 (d,k,r), 1.62 (e,l,s), 2.23 (f,m,t), and 4.0 (g,n,u).
The ESI+
fully illustrate the
dynamics
of compression
and decompression.
|