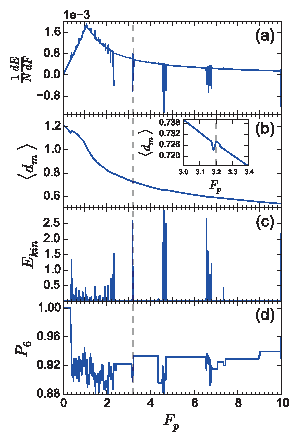
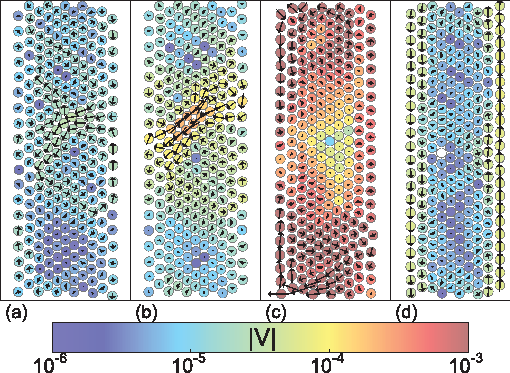
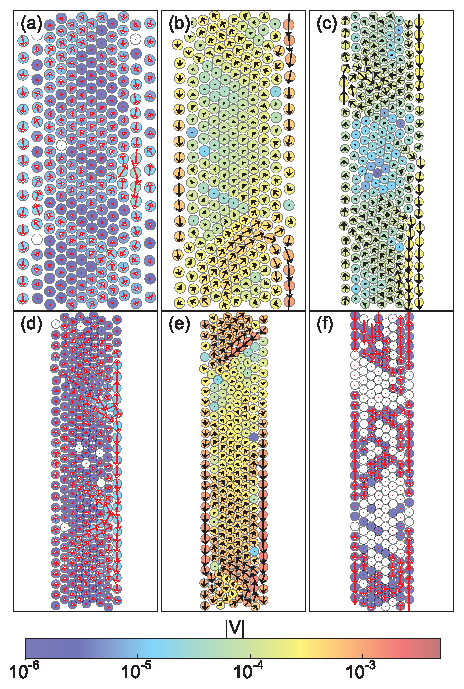
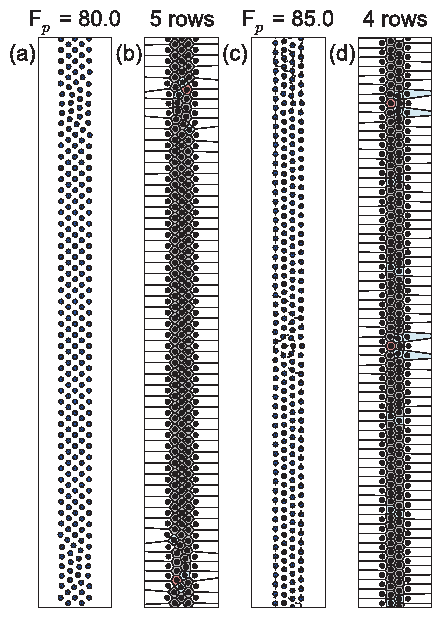
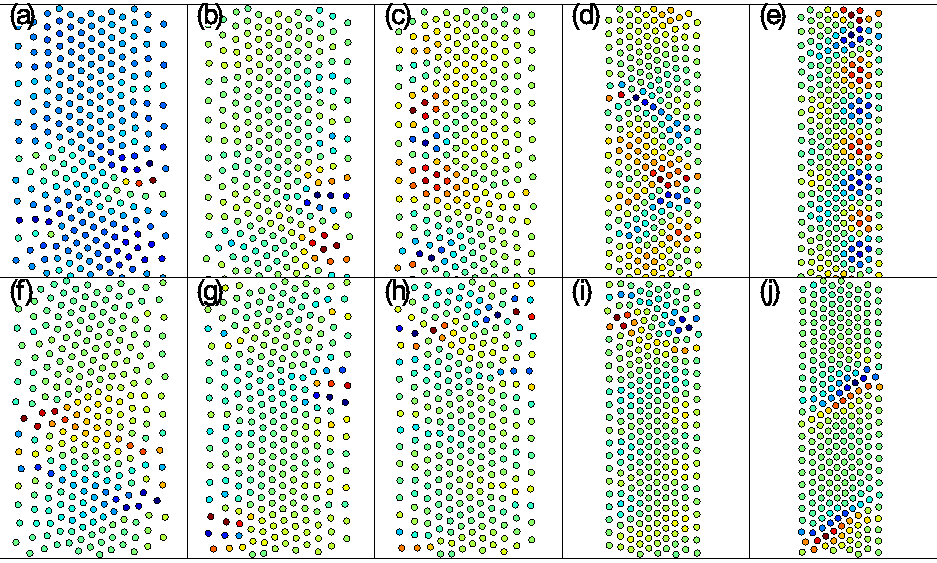
 Figure 12:
Images illustrating the hysteretic behavior
of the sample shown in Fig. 11(c) over the range
Fp=1.5 to Fp=4.0.
Particle positions are colored by Vx,
and are scaled within each image to maximize the features.
Blue particles have relatively large negative Vx,
green particles move slowly,
and red particles have relatively large positive Vx.
In (a-e) the system is being compressed while in (f-j) the system
is being decompressed.
(a,f) At Fp = 1.5 there are roughly 13 rows of particles that are
not fully oriented along the y axis.
(b,g) At Fp = 1.6 there is a mixture of vertical and diagonal
rows of particles, accommodated by edge dislocations.
There are 13 rows of particles during compression in panel (b), while there
are only 12 rows of particles during decompression in panel (g).
(c,h) A similar mixture of vertical and diagonal particle
rows appears at Fp = 1.7.
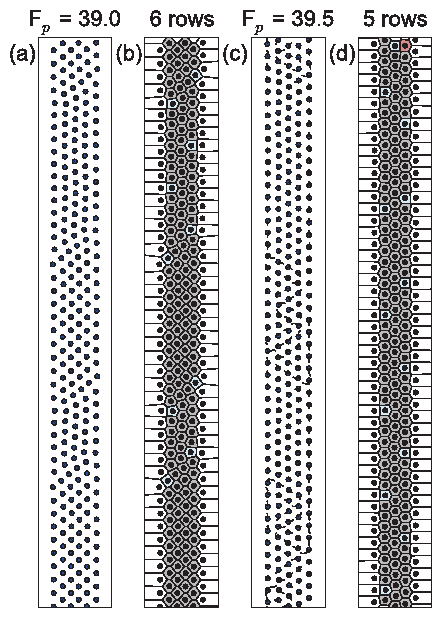
(d,i) At Fp = 3.2 the rows have become fully vertical, and there are
11 rows during compression but only 10 during decompression.
(e,j) At Fp = 4.0, there are 10 rows during compression and 9 rows
during decompression.
Figure 12:
Images illustrating the hysteretic behavior
of the sample shown in Fig. 11(c) over the range
Fp=1.5 to Fp=4.0.
Particle positions are colored by Vx,
and are scaled within each image to maximize the features.
Blue particles have relatively large negative Vx,
green particles move slowly,
and red particles have relatively large positive Vx.
In (a-e) the system is being compressed while in (f-j) the system
is being decompressed.
(a,f) At Fp = 1.5 there are roughly 13 rows of particles that are
not fully oriented along the y axis.
(b,g) At Fp = 1.6 there is a mixture of vertical and diagonal
rows of particles, accommodated by edge dislocations.
There are 13 rows of particles during compression in panel (b), while there
are only 12 rows of particles during decompression in panel (g).
(c,h) A similar mixture of vertical and diagonal particle
rows appears at Fp = 1.7.
(d,i) At Fp = 3.2 the rows have become fully vertical, and there are
11 rows during compression but only 10 during decompression.
(e,j) At Fp = 4.0, there are 10 rows during compression and 9 rows
during decompression.
|