Physical Review Letters 120, 117203 (2018)

Avalanches and Criticality in Driven Magnetic Skyrmions

S. A. Díaz1,2, C. Reichhardt1, D. P. Arovas2, A. Saxena1 and C. J. O. Reichhardt1

1Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Department of Physics, University of California San Diego, La Jolla, California 92093, USA

(Received 6 December 2017; published 15 March 2018)

We show using numerical simulations that slowly driven skyrmions interacting with random pinning move via correlated jumps or avalanches. The avalanches exhibit power law distributions in their duration and size, and the average avalanche shape for different avalanche durations can be scaled to a universal function, in agreement with theoretical predictions for systems in a nonequilibrium critical state. A distinctive feature of skyrmions is the influence of the non-dissipative Magnus term. When we increase the ratio of the Magnus term to the damping term, a change in the universality class of the behavior occurs, the average avalanche shape becomes increasingly asymmetric, and individual avalanches exhibit motion in the direction perpendicular to their own density gradient.
Introduction
Simulation and system
Results
Summary
References


Introduction. Magnetic skyrmions are nanoscale particlelike spin textures that were first observed in chiral magnets in 2009 [1,2] and have since been identified in a growing variety of materials, including several that support skyrmions at room temperature [3,4,5,6,7,8]. Skyrmions can exhibit depinning phenomena under an applied current [2,9,10,11,12,13,14,15,16], and their ability to be set in motion along with their size scale make them promising candidates for a variety of applications [17,18]. A key feature of skyrmions that is distinct from other depinning systems [19] is the strong influence on the skyrmion motion of the non-dissipative Magnus term, which arises from the skyrmion topology [2]. Strong Magnus terms are also relevant for vortex depinning in neutron star crusts [20,21]. In particle-based models of vortices in type-II superconductors or colloidal particles, the motion is dominated by the damping term which aligns the particle velocity with the external forces [19]. In contrast, the Magnus term aligns the particle velocity perpendicular to the direction of the external forces, causing the skyrmions to move at an angle called the intrinsic skyrmion Hall angle θintSk with respect to the external forces [2,10,12,13,14]. As recently shown, the Magnus term strongly affects the overall skyrmion dynamics in the presence of disorder, with the measured skyrmion Hall angle starting at zero or a small value for drives just above depinning and gradually increasing to the intrinsic or pin-free θintSk value as the drive increases and the skyrmions move faster [12,13,14,15,16,22,23,24,25].
In many slowly driven systems with quenched disorder, the motion near depinning takes the form of bursts or avalanches of the type observed in driven magnetic domain walls [26,27,28], vortices in type-II superconductors [19,29,30,31], earthquake models [32], and near yielding transitions in sheared materials [33,34]. Avalanches or so-called crackling noise arise in a wide range of collectively interacting driven systems, and scaling properties of the avalanche size distributions as well as the average avalanche shape can be used to determine whether the system is at a nonequilibrium critical point and to identify its universality class [35,36,37]. In many avalanche systems, the dynamics is overdamped, but when non-dissipative effects become important, the statistics of the avalanches can change. In particular, the average avalanche shape becomes asymmetric in the presence of an effective mass or stress overshoots [28,36,37]. An open question is whether skyrmions can exhibit avalanche dynamics and, if so, what impact the Magnus term would have on such dynamics. It is important to understand intermittent skyrmion dynamics near the depinning threshold in order to fully realize applications which require skyrmions to be moved and stopped in a controlled fashion, such as in skyrmion race track memories [18].
In this work we numerically examine avalanches of slowly driven skyrmions moving over quenched disorder for varied ratios αm/αd of the Magnus term to the damping term. When αm/αd ≤ 1.73, corresponding to intrinsic skyrmion Hall angles of θintSk ≤ 600, the skyrmion avalanches are power law distributed in both size and duration, and the average avalanche shape for a fixed duration can be scaled to a universal curve as predicted for systems in a nonequilibrium critical state [35,36,37]. For larger values of the Magnus term, the avalanches develop a characteristic size and the average avalanche shape becomes strongly asymmetric, indicative of an effective negative mass similar to that observed for avalanche distributions in certain domain wall systems [28].
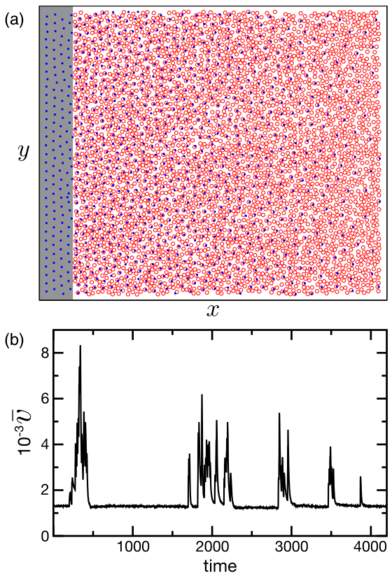
Fig1.png
Figure 1: (a) Snapshot of the system showing the skyrmions (solid dots) and pinning sites (open circles). Skyrmions are introduced in the unpinned region on the left side of the sample and removed when they reach the right side of the sample. Once the system reaches a steady state, individual skyrmions are added at a slow rate. (b) A segment of the time series of the net skyrmion velocity, ―v, versus time in simulation time steps. Clear skyrmion avalanche events appear.
Simulation and system. In Fig. 1 we show a snapshot of our 2D system which has periodic boundary conditions only in the y-direction and contains N skyrmions interacting with Np randomly placed pinning sites. The skyrmions are modeled as particles with dynamics governed by the modified Thiele equation, used previously to study skyrmions interacting with random [12,16] and periodic [23,24] pinning substrates. The equation of motion of a single skyrmion i is:
αd vi − αm
^
z
 
 ×vi = Fssi + Fspi .
(1)
Here ri is the skyrmion position and vi = d ri/dt is the skyrmion velocity. The damping constant is αd while αm is the strength of the Magnus term. In the absence of pinning, a skyrmion experiencing a uniform external force moves at the intrinsic skyrmion Hall angle of θintSk = tan−1(αm/αd) with respect to the direction of the external force, and in the overdamped limit of αm = 0, θintSk = 0°. The skyrmion-skyrmion repulsive interaction force is given by Fssi = ∑Nj=1 K1(rij) ∧rij where rij=|ri − rj|, ∧rij=(ri − rj)/rij, and K1 is a modified Bessel function. The pinning force from the quenched disorder Fspi arises from Np randomly placed non-overlapping harmonic traps with maximum pinning force Fp and radius Rp = 0.15. The system dimensions are Lx = 26 and Ly = 24, and there is a pin-free region extending from x=0 to x=4. An artificial wall of stationary skyrmions is placed to the left of x=0 to provide confinement. The skyrmions are driven by a gradient, introduced by slowly dropping skyrmions into the pin-free region and allowing them to move into the pinned region under the force of their mutual repulsion[38]. Skyrmions that reach the right edge of the sample are removed from the simulation. After the system reaches a steady state, which typically requires 2 ×103 skyrmion drops, we examine individual avalanches by measuring the net skyrmion velocity response ―v=N−1∑i=0N|vi| between drops, as illustrated in Fig. 1(b). We drop skyrmions at a slow enough rate that the time series ―v(t) shows well-defined avalanches separated by intervals of no motion. We consider five different intrinsic skyrmion Hall angles θintSk = 0°, 30°, 45°, 60°, and 80°, where we fix αd = 1.0 and vary αm. We studied several different pinning densities and strengths, but here we focus on systems with Np = 3700 and Fp = 1.0. Experimentally our system corresponds to skyrmions entering from the edge of a sample or moving from a pin-free to a pinned region of the sample driven by a slowly changing magnetic field or small applied current.
Fig2.png
Figure 2: (a) Average avalanche size 〈S〉 vs avalanche duration T for θintSk = 30°. Dashed line is a fit to 〈S〉 ∝ T1/σνz with 1/σνz = 1.63. (b) Distribution of avalanche durations P(T) and (c) distribution of avalanche sizes P(S) for θintSk = 0°, 30°, 45°, 60°, and 80°, from bottom to top. The curves have been shifted vertically for clarity. (d) The scaling exponents τ (triangles), α (squares), and 1/σνz (circles) vs θintSk. For θintSk ≤ 60°, α = 1.5, τ = 1.33, and 1/σνz = 1.63, while for θintSk = 80°, α = 2.5, τ = 1.6, and 1/σνz = 2.4.
Results. From the time series of the skyrmion velocity ―v(t) we determine the avalanche duration T as the time during which ―v > vth, where vth is a threshold velocity. We define the avalanche size S as the time integral S = ∫t0t0+T ―v(t) − vth over the duration of the avalanche. Near a critical point, various quantities associated with the avalanches are expected to scale as power laws [35]: the average avalanche size 〈S〉(T) ∝ T1/σνz, the distribution of avalanche durations P(T) ∝ T−α, and the avalanche size distribution P(S) ∝ S−τ. In Fig. 2(a) we plot 〈S〉 versus T for a system with θintSk = 30° , while Figs. 2(b,c) show the corresponding P(T) and P(S) for θintSk = 0° to 80°. In each case we find a range of power law scaling. In Fig. 2(d) we plot the extracted critical exponents τ, α, and 1/σνz versus θintSk. The exponents are roughly constant for θintSk ≤ 60° with τ = 1.33, α = 1.5, and 1/σνz = 1.63. For θintSk = 80°, we find longer avalanches of larger size, as indicated by the changes in P(T) and P(S), while P(T) develops a maximum due to the emergence of a characteristic avalanche size. If we consider only the larger avalanches from the θintSk = 80° sample, we obtain considerably larger exponents of 1/σνz = 2.4, α ≈ 2.5, and τ = 1.6, as shown in Fig. 2(d). The exponents for a system in a critical state are predicted to satisfy the following relation[35]:
α−1
τ−1
 = 1
σνz
 .
(2)
Samples with θintSk < 60° obey this relation, samples with θintSk = 60° give 1.55 for the right hand side and 1.63 for the left hand side, and samples with θ = 80° again obey this relation.
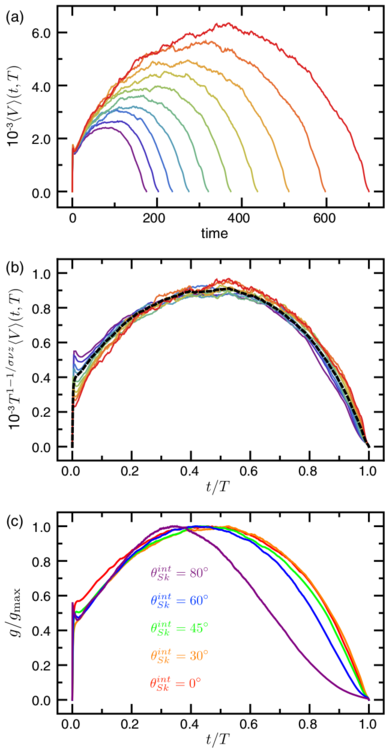
Fig3.png
Figure 3: (a) The time averaged avalanche velocity 〈V〉(t,T) in a system with θintSk=30°, for avalanches of duration T, versus time in simulation time steps. The curves represent the time average over ten logarithmically-spaced bins for T = 150, 175, 204, 238, 278, 324, 378, 441, 514, 600, and 700 simulation time steps, from left to right. (b) Scaling collapse of the data in panel (a) plotted as T1 − 1/σνz〈V〉(t,T) vs t/T, where 1/σνz = 1.63. The dashed curve indicates the overall average avalanche shape. (c) The average avalanche shapes g/gmax vs t/T for θintSk = 0° (red), 30° (orange), 45° (green), 60° (blue), and 80° (purple).
A more stringent test of whether a system is at a nonequilibrium critical point is the prediction that the average avalanche shape can be scaled to a universal curve [35,36,37]. This implies that the average skyrmion velocity for a given avalanche duration should scale as 〈V〉(t,T) ∝ T1/σνz − 1g(t/T), where g(t/T) is a universal function of the avalanche shape that can be extracted from the time series by plotting T1 − 1/σνz〈V〉(t,T) versus t/T. In Fig. 3(a) we plot the average avalanche shape 〈V〉 for different values of T in the θintSk = 30° system, and in Fig. 3(b) we show a scaling collapse of the same data versus t/T. The dashed line is a fit to the overall average avalanche shape g(t/T). We performed similar scaling collapses for other values of θintSk and find the same universal function g(t/T) for θintSk ≤ 60°, as shown in Fig. 3(c), while for θintSk = 80°, the average avalanche shape is much more asymmetric.
Fig4.png
Figure 4: Snapshots of the avalanche motion during a single large avalanche. Blue dots indicate skyrmions that did not move during the avalanche event, red dots indicate skyrmions that moved a distance greater than x, and lines indicate the net displacement of individual skyrmions during the avalanche. (a) θintSk = 0°. (b) θintSk = 30°. (c) θintSk=60°. (d) θintSk = 80°. As the Magnus term increases, the avalanche motion starts to show curvature in the positive y direction.
The change in the exponents and the average avalanche shape for large θintSk indicates that when the non-dissipative Magus term is strong, there is a change in the universality class. Mean field predictions give τ = 1.5, α = 2.0, 1/σνz = 2.0, and a parabolic universal function for the average avalanche shape [39,40]. In our system, τ = 1.33, α = 1.5, 1/σνz = 1.63, and the universal function g(t/T) has a parabolic shape with some asymmetry at small t/T. Since we are working in two dimensions and the skyrmion interaction range is finite, it may be expected that our system would not match the mean field picture; however, it is clear that when the Magnus term is large, the avalanche dynamics show a pronounced change. The asymmetry in the scaling collapse of the avalanches is similar to that found in many systems including magnetic domain avalanches, where it was argued to result from an effective negative mass [28]. Inertial effects with positive mass tend to give a leftward asymmetry, while an effective negative mass damps the avalanches at later times and produces a rightward asymmetry [28]. The Magnus term causes the skyrmions to move in the direction perpendicular to the applied external force, and this could reduce the overall avalanche motion in the forward direction at later times, resulting in the skewed average avalanche shape. In Fig. 4(a) we plot the skyrmions and their net displacements during a large avalanche in a sample with θintSk = 0°, where the motion strongly follows the density gradient from left to right. At θintSk=30° in Fig. 4(b), near the right edge of the sample the avalanche motion shows a tendency to curve in the positive y direction. This tendency is enhanced for θintSk=60° in Fig. 4(c) and for θintSk=80° in Fig. 4(d), where the entire avalanche moves at an angle with respect to the x axis.
We have examined several other pinning landscapes, including samples with the same Np=3700 but a lower Fp=0.3, where we find results similar to those of the Fp=1.0 system. In the limit of strong dilute pinning with Np=600 and Fp=3.0, skyrmions that become pinned generally never depin and we observe a strong channeling effect where the avalanches occur through the motion of interstitial or unpinned skyrmions moving along weak links between pinned skyrmions. In this case, the distribution of avalanche sizes is strongly peaked at the size corresponding to the weak link channel.
There are several experimental possibilities for investigating avalanches in skyrmion systems. Direct imaging experiments have already revealed that skyrmions entering from the edge of the sample appear to undergo sudden rearrangements, while other experiments have successfully tracked individual driven skyrmions, so that it should be possible to image avalanche dynamics just above the threshold for skyrmion motion [13,41,42]. Electrical detection of skyrmion motion near the depinning threshold was achieved in recent experiments, and could be used to probe for the existence of avalanche statistics as a function of increasing or decreasing current or field [43,44]. Avalanches can also produce jumps in magnetization curve measurements [45]. Additionally, recently developed imaging techniques are able to detect avalanchelike dynamics as a function of changing field [46]. It could also be possible to fabricate samples containing one region of low pinning and another region of enhanced pinning introduced via irradiation, and then perform direct imaging of skyrmion avalanches produced as the skrymions pass from one region to the other. Electrical measurements could reveal how the avalanche statistics change as the amount of added disorder is varied.
Summary- We have shown that skyrmions driven by their own gradient in the presence of quenched disorder exhibit avalanche dynamics and show power law avalanche duration and size distributions. The average avalanche shape for different avalanche durations can be scaled by a universal function, in agreement with predictions for systems near a nonequilibrium critical point. Skyrmions are distinct from previously studied avalanche systems due to the strong non-dissipative Magnus term in the skyrmion dynamics. We find that as the Magnus term increases, there is a change in the critical behavior of the avalanches as indicated by the critical exponents, and the average avalanche shape develops a strong asymmetry similar to that found for a negative effective mass in magnetic domain depinning avalanches. This change in behavior results when the Magnus term causes the avalanche motion to shift partially into the direction perpendicular to the skyrmion density gradient.
We thank Karin Dahmen for useful discussions. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Science 323, 915 (2009).
[2]
N. Nagaosa and Y. Tokura, Nat. Nanotechnol. 8, 899 (2013).
[3]
X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Nature (London) 465, 901 (2010).
[4]
W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F. Y. Fradin, J. E. Pearson, Y. Tserkovnyak, K. L. Wang, O. Heinonen, S. G. E. te Velthuis, and A. Hoffmann, Science 349, 283 (2015).
[5]
Y. Tokunaga, X. Z. Yu, J. S. White, H. M. Rønnow, D. Morikawa, Y. Taguchi, and Y. Tokura, Nat. Commun. 6, 7638 (2015).
[6]
S. Woo, K. Litzius, B. Kruger, M. Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R. M. Reeve, M. Weigand, P. Agrawal, I. Lemesh, M. A. Mawass, P. Fischer, M. Klaui, and G. R. S. D. Beach, Nat. Mater. 15, 501 (2016).
[7]
O. Boulle, J. Vogel, H. Yang, S. Pizzini, D. de S. Chaves, A. Locatelli, T. O. Mentes, A. Sala, L. D. Buda-Prejbeanu, O. Klein, M. Belmeguenai, Y. Roussigné, A. Stashkevich, S. M. Chérif, L. Aballe, M. Foerster, M. Chshiev, S. Auffret, I. M. Miron, and G. Gaudin, Nat. Nanotech. 11, 449 (2016).
[8]
A. Soumyanarayanan, M. Raju, A. L. Gonzalez-Oyarce, A. K. C. Tan, M.-Y. Im, A. P. Petrovi\'c, P. Ho, K. H. Khoo, M. Tran, C. K. Gan, F. Ernult and C. Panagopoulos, Nat. Mater. 16, 898 (2017).
[9]
T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, and A. Rosch, Nat. Phys. 8, 301 (2012).
[10]
J. Iwasaki, M. Mochizuki, and N. Nagaosa, Nat. Commun. 4, 1463 (2013).
[11]
D. Liang, J. P. DeGrave, M. J. Stolt, Y. Tokura, and S. Jin, Nat. Commun. 6, 8217 (2015).
[12]
C. Reichhardt, D. Ray, and C. J. O. Reichhardt, Phys. Rev. Lett. 114, 217202 (2015).
[13]
W. Jiang, X. Zhang, G. Yu, W. Zhang, X. Wang, M. B. Jungfleisch, J. E. Pearson, X. Cheng, O. Heinonen, K. L. Wang, Y. Zhou, A. Hoffmann, and S. G. E. te Velthuis, Nat. Phys. 13, 162 (2017).
[14]
K. Litzius, I. Lemesh, B. Krüger, P. Bassirian, L. Caretta, K. Richter, F. Büttner, K. Sato, O. A. Tretiakov, J. Förster, R. M. Reeve, M. Weigand, I. Bykova, H. Stoll, G. Schütz, G. S. D. Beach, and M. Kläui, Nat. Phys. 13, 170 (2017).
[15]
W. Legrand, D. Maccariello, N. Reyren, K. Garcia, C. Moutafis, C. Moreau-Luchaire, S. Collin, K. Bouzehouane, V. Cros, and A. Fert, Nano. Lett. 17, 2703 (2017).
[16]
S. A. Díaz, C. J. O. Reichhardt, D. P. Arovas, A. Saxena, and C. Reichhardt, Phys. Rev. B 96, 085106 (2017).
[17]
A. Fert, V. Cros, and J. Sampaio, Nat. Nanotechnol. 8, 152 (2013).
[18]
A. Fert, N. Reyren, and V. Cros, Nat. Rev. Mater. 2, 17031 (2017).
[19]
C. Reichhardt and C. J. O. Reichhardt, Rep. Prog. Phys. 80, 026501 (2017).
[20]
G. Wlazlowski, K. Sekizawa, P. Magierski, A. Bulgac, and M. McNeil Forbes, Phys. Rev. Lett. 117, 232701 (2016).
[21]
M.A. Sheikh, R.L. Weaver, and K.A. Dahmen, Phys. Rev. Lett. 117, 261101 (2016).
[22]
J. Müller and A. Rosch, Phys. Rev. B 91, 054410 (2015).
[23]
C. Reichhardt, D. Ray, and C. J. O. Reichhardt, Phys. Rev. B 91, 104426 (2015).
[24]
C. Reichhardt and C. J. O. Reichhardt, New J. Phys. 18, 095005 (2016).
[25]
J.-V. Kim and M.-W. Yoo, Appl. Phys. Lett. 110, 132404 (2017).
[26]
J. P. Sethna, K. A. Dahmen, and C. R. Myers, Nature 410, 242 (2001).
[27]
S. Zapperi, P. Cizeau, G. Durin, and H. E. Stanley, Phys. Rev. B 58, 6353 (1998).
[28]
S. Zapperi, C. Castellano, F. Colaiori, and G. Durin, Nat. Phys. 1, 46 (2005).
[29]
S. Field, J. Witt, F. Nori, and X.S. Ling, Phys. Rev. Lett. 74, 1206 (1995).
[30]
C.J. Olson, C. Reichhardt, and F. Nori, Phys. Rev. B 56, 6175 (1997).
[31]
E. Altshuler and T. H. Johansen Rev. Mod. Phys. 76, 471 (2004).
[32]
D.S. Fisher, Phys. Rep. 301, 11 (1998).
[33]
M.-C. Miguel, A. Vespignani, S. Zapperi, J. Weiss, and J.-R. Grasso, Nature 410, 667 (2001).
[34]
M. Zaiser, Adv. Phys. 55, 185 (2006).
[35]
J. P. Sethna, K. A. Dahmen, and C. R. Myers, Nature 410, 242 (2001).
[36]
A. P. Mehta, A. C. Mills, K. A. Dahmen, and J. P. Sethna, Phys. Rev. E 65, 046139 (2002).
[37]
S. Papanikolaou, F. Bohn, R. L. Sommer, G. Durin, S. Zapperi, and J. P. Sethna, Nat. Phys. 7, 316 (2011).
[38]
C.J. Olson, C. Reichhardt, and F. Nori, Phys. Rev. B 56, 6175 (1997).
[39]
K. A. Dahmen, Y. Ben-Zion, and J. T. Uhl, Phys. Rev. Lett. 102 , 175501 (2009).
[40]
K. A. Dahmen, Y. Ben-Zion, and J. T. Uhl, Nat. Phys. 7, 554 (2011).
[41]
X.Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W.Z. Zhang, S. Ishiwata, Y. Matsui, and Y. Tokura, Nat. Mater. 10, 106 (2011).
[42]
R. Tolley, S.A. Montoya, and E.E. Fullerton, arXiv:1711.07101 (unpublished).
[43]
K. Zeissler et al., arXiv:1706.06024 (unpublished).
[44]
D. Maccariello et al., Nat. Nanotech., in press (2018) doi:10.1038/s41565-017-0044-4.
[45]
K. Zeissler et al., arXiv:1706.01065 (unpublished).
[46]
J. Lee et al, Scaling of domain cascades in stripe and skyrmion phases, Bull. Am. Phys. Soc. (March Meeting, 2018).


File translated from TEX by TTHgold, version 4.00.
 Back to Home