Physica C 290, 89 (1997)

Plastic flow, voltage bursts, and vortex avalanches in superconductors

C. J. Olson¹, C. Reichhardt¹, J. Groth¹, Stuart B. Field^1,2, and Franco Nori¹
¹Department of Physics, The University of Michigan, Ann Arbor, Michigan 48109-1120
²Department of Physics, Colorado State University, Fort Collins, Colorado 80523^f

Received 16 July 1997; accepted 21 July 1997

Abstract

We use large-scale parallel simulations to compute the motion of superconducting magnetic vortices during avalanches triggered by small field increases. We relate observations of pulsing vortex movement in winding chains to features of statistical distributions and experimentally observable voltage noise. As pin density is increased, the very broad distribution of avalanche sizes begins to develop typical avalanche sizes. We show that this corresponds to a crossover from pin-to-pin motion in broad channels to interstitial motion in narrow easy-flow channels. Our results are consistent with recent experiments.
PACS: 64.60.Ht; 74.60.Ge

1. Introduction and summary of results
2. Simulation
3. Channels
4. Avalanche lifetimes
5. Displacements
6. Number of vortices leaving the sample
7. Relation to experiment
8. Voltage noise power
9. Conclusions
References

1. Introduction and summary of results

Recent studies of a variety of physical systems characterized by avalanche dynamics have revealed many interesting dynamical behaviors. Plastic motion, burst-like behavior and broad distributions of event sizes have been observed in systems such as granular assemblies [1,2,3], magnetic domains [4], fluid flow [5,6], and flux lines in type-II superconductors [7,8,9,10,11,12,13]. Although all of these systems display avalanches, changes in the experimental conditions or variations from sample to sample result in the observation of different forms of avalanche size distributions or different spectral signatures in the same system. There is considerable interest in determining what microscopic properties of the different samples are responsible for the macroscopically observed differences. It has, however, not been feasible experimentally to determine the microscopic motion of the individual grains, domain walls, fluid drops or flux lines, while still collecting macroscopic information over time scales long enough to statistically characterize the system, and so no direct experimental evidence of the microscopic nature of the observed changes is available. It is therefore natural to turn to numerical simulations in which it is possible to obtain detailed dynamical information while also precisely controlling the microscopic parameters.

Early avalanche simulations used simple discrete models [14] and the small number of simulations employing more realistic continuous molecular dynamics (MD) models were highly restricted in the number of particles used and avalanche events recorded. None of the MD simulations examined the power spectra of the noise signal, an important quantity that is readily accessible in experiments. The simulation presented in this paper overcomes these limitations. With our highly optimized, parallel MD simulation of superconducting vortex avalanche dynamics, we studied samples containing a large number of pins (up to 3700) and vortices (up to 1800). We collected detailed information on both vortex positions and voltage noise information for a much greater number of distinct avalanches (~ 50 000) than has ever been obtained in an MD avalanche simulation. This provides a unique opportunity to directly compare microscopic information with the longer-time statistical information collected in experiments. By varying the pinning density n_p and maximum pinning strength f_p, we obtain avalanche distributions and voltage noise spectra in good agreement with recent experiments [7,12,13], and quantify how the density and strength of pinning sites affects both the breadth of these distributions and the shape of the noise spectra. Characteristic avalanche sizes and lifetimes, along with a change in the form of the voltage spectra, appear at low pin densities when narrow winding channels of interstitial vortices form. At higher pin densities, pin-to-pin transport through vortex chains occurs, and a crossover in the avalanche size and lifetime distributions occurs to a very broad distribution. We find that there is no universal distribution valid for all pinning parameters.

Although we focus specifically on superconducting avalanches in this paper, our system features many aspects that are relevant to other systems that display avalanche dynamics, including the burst-like behavior, broad-band noise and braod distributions of avalanche sizes. Additionally, the channel structures that we observe in this system have analogs in other non-superconducting systems undergoing avalanches, such as when drops of water roll down a slope, or when a localized portion of sand slides down the edge of a sandpile.

2. Simulation

As an external field is slowly increased, a metastable gradient in vortex density, termed the Bean state [15], forms inside a type-II superconductor as vortices are driven into the sample by their mutual repulsion and are held back by defects in the material [7,8,9,10,11,12]. The competition between pinning and driving forces resembles that found in many other systems that display intermittent or avalanche-like behavior. To model this system, we simulate an infinite slab with a magnetic field H=H∧z applied parallel to the surface so that there are no demagnetization effects. The rigid vortices and straight columnar pins we consider are all parallel to ∧z, so we can obtain all relevant dynamical information from a transverse two-dimensional slice, in the x-y plane, of the three-dimensional slab. The flux lines evolve according to a T=0 MD algorithm. The vortex-vortex repulsion, given by the modified Bessel function K₁(r/λ), is cut off beyond r=6λ, where λ is the penetration depth, so that each vortex interacts with up to 100 neighbors, and important collective effects, neglected in simulations with shorter interaction ranges, are observed. Each 24λ×26λ sample contains up to 3700 attractive parabolic pins of radius ξ_p=0.15λ with pinning densities n_p=0.96/λ², n_p=2.40/λ², or n_p=5.93/λ², and pinning strengths uniformly distributed over the range f_p^max/5 to f_p^max, where f_p^max=0.3f₀, 1.0f₀, or 3.0f₀. All forces are given in units of f₀=Φ₀²/8π²λ³ and lengths in units of λ.

The total force on vortex i is given by

f_i=f_i^vv + f_i^vp=ηv_i ,

(1)

where the force on vortex i from other vortices is

f_i^vv

N_v
∑
j=1

f₀ K₁

⎛
⎝

|r_i − r_j |

⎞
⎠

and the force from pinning sites is

f_i^vp =

N_p
∑
k=1

f_p

ξ_p

|r_i − r_k^(p)| Θ

⎛
⎝

ξ_p − |r_i − r_k^(p) |

⎞
⎠

(2)

Here, Θ is the Heaviside step function, r_i (v_i) is the location (velocity) of vortex i, r_k^(p) is the location of pinning site k, there are N_p pinning sites and N_v vortices, ∧r_ij=(r_i−r_j)/|r_i−r_j|, ∧r_ik=(r_i−r_k^(p))/|r_i−r_k^(p)|, and we take η = 1. We have taken advantage of the cut-off on the vortex interaction range to parallelize our code. Using a one-dimensional domain decomposition, we divide the sample into strips that are multiples of the interaction range in width, place each strip on a separate node, and use message passing techniques at the processor boundaries. Load balancing is simplified by the repulsive nature of the interaction which tends to spread the vortices evenly among the processors. With the flexible domain decomposition, the number of processors can be varied without affecting the results. Using roughly 10⁴ hours on an IBM SP parallel computer, we recorded more than 10⁴ avalanches for each of five combinations of n_p and f_p.

A slowly increasing external field is modeled by adding a single vortex to an unpinned region along the sample edge whenever the system reaches mechanical equilibrium [16,17,18,19] (we consider dynamical, not thermal, instabilities). This is analogous to adding a single grain of sand to a pile. Most of these small field increases result in only slight shifts in vortex positions, but occasionally one or more vortices become depinned, producing an avalanche. We find that avalanche disturbances propagate as an uneven pulse, as seen in Fig. 4 of Ref. [16]. Events with longer lifetimes often contain more than one pulse of motion (i.e., multiple oscillations in the total avalanche velocity) [20]. By imaging individual avalanches in our samples, we find that a chain of vortices is displaced in a typical event. Each vortex in the chain is depinned, moves a short distance, and comes to rest in a nearby pinning site. Vortices outside the chain transmit stress by shifting very slightly inside pinning sites, but are not depinned. Chain size varies from event to event: in some cases a chain spans the sample, while in other events the chain contains only three or four vortices. In each case, although the disturbance may cross the sample, an individual vortex does not. Thus, the time span of a typical avalanche is much shorter than the time a single vortex takes to traverse the sample.

3. Channels

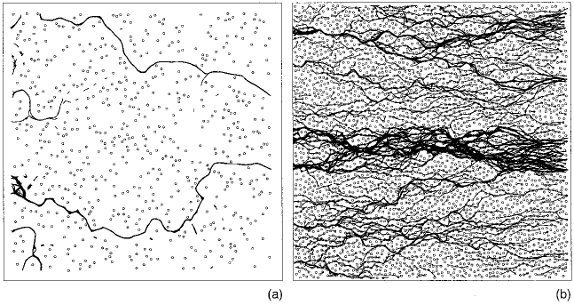Fig. 1: Continuous lines indicate the paths vortices follow over an extended period of time covering many avalanches through two 24λ×26λ samples with f_p^max=3.0f₀ and different pinning densities: (a) n_p=0.96/λ² and (b) n_p=5.93/λ². Open circles mark pinning sites. The presence or absence of easy-flow channels is clearly dependent on pin density. The channels present in (a) lead to avalanches with characteristic sizes and lifetimes superimposed on a broad distribution. Samples with higher pinning density produce very broad distributions of avalanche sizes.

When the pinning density is high, chains of moving vortices are equally likely to form anywhere in the sample. As the pinning density is lowered, vortices move only through well-defined winding interstitial channels in which vortices are weakly held in place only by the repulsion of other vortices which sit in pinning sites. To identify the cumulative pattern of flow channels for different pinning parameters, in Fig. 1 we plot vortex trajectories with lines over the course of many avalanches. A concentration of trajectory lines indicates a heavily-travelled region of the sample. In Fig. 1a we show a sample with low pinning density. We see that all motion occurs through narrow easy-flow interstitial channels. In these channels, mobile interstitial vortices move plastically [21,22,23,24,25] (note, in relation to Ref. [25], that in our work, vortices are flux-gradient-driven, with no artificial 'uniform force' applied to them) around their strongly pinned neighbors in a manner similar to that recently imaged experimentally [10,11]. As the pin density increases, the amount of interstitial pinning decreases and the number of channels increases, until at high pin densities (Fig. 1b), there is no interstitial flow and the vortices move only from pin to pin. Here, where no well-defined easy-flow channel exists, avalanches are spread evenly throughout the sample.

4. Avalanche lifetimes

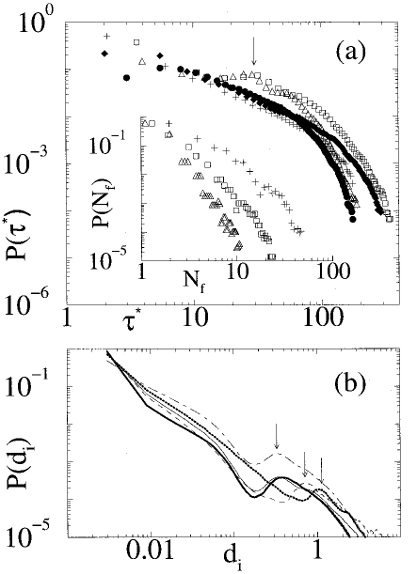Fig. 2: Avalanche distributions: (a) lifetimes τ^*; (b) individual vortex displacements d_i. Inset of (a); number N_f of vortices falling off the edge of the sample. Solid symbols refer to samples with high pin density n_p=5.93/λ², and differing pinning strengths: plus signs (heavy solid line), f_p^max=3.0f₀; filled diamonds (solid line), f_p^max=1.0f₀; filled circles (dot-dashed line), f_p^max=0.3f₀. Open symbols refer to samples with f_p^max=3.0f₀ and varying pinning densities: plus signs (heavy solid line), n_p=5.93/λ²; open squares (dashed line), n_p=2.40/λ²; open triangles (heavy dotted line), n_p=0.96/λ².

We determine how the microscopic pinning parameters affect avalanche size by finding the total avalanche lifetime τ for each event. Since vortices typically move, or 'hop', from pin to pin in samples with high pinning density, a natural unit of time is the interval t_h a vortex spends hopping between pinning sites, and so we use scaled lifetimes τ^*=τ/t_h. To find t_h, we assume that each vortex hops a distance d_p = n_p^−1/2, the average distance between pinning sites, and that the vortex speed v_c is proportional to the depinning force,

v_c=

|f_i|

(3)

where |f_i| ≈ −f_p. This gives

t_h=

d_p

v_c

≈ ηf_p⁻¹ n_p^−1/2. ,

(4)

The plot of P(τ^*) in Fig. 2(a) for samples with dense pinning shows that in each case the distribution is very broad and can be written as

P(τ^*) ∼ (τ^*)^−1.4

(5)

over a range of τ^*. The form of P(τ^*) changes noticeably when the pinning density n_p is reduced, and an enhanced probability for avalanches with a characteristic value (arrow in Fig. 2a) arises as a result of the appearance of easy-flow interstitial channels. Many avalanches in these samples consist of a single sample-spanning pulse of motion through one of these channels, seen in Fig. 1a. The estimated pulse lifetime produced by a straight channel is

τ_est ≈ t_h N_h,

(6)

where N_h is the number of vortices in the channel. Since

N_h ≈ L_x√{n_v},

(7)

where L_x is the sample length, we find

τ_est ≈ ηL_x f_p⁻¹√{n_v/n_p},

(8)

which gives a characteristic value of

τ^* = τ_est/t_h ≈ L_x√{n_v}=26λ√{1.5/λ²} ≈ 30.

(9)

This value agrees well with the peak in the distribution of τ^*, indicated by an arrow in Fig. 2a.

5. Displacements

For all pin densities, only a small fraction of the vortices move significantly while the rest shift in pinning sites, as seen by considering the distance d_i each vortex is displaced in an avalanche. Vortices that hop from pin to pin create a peak in P(d_i), marked with arrows in Fig. 2b, at

d_i ≈ d_p = n_p^−1/2.

(10)

For those vortices that remain pinned and accumulate stress in the vortex lattice, d_i < d_p, we can approximate the distribution by

P(d_i) ∼ d_i^−ρ,

(11)

where ρ ∼ 1.4 for all samples except ρ ∼ 1.2 for [n_p=0.96/λ², f_p^max=3.0f₀], and ρ ∼ 0.9 for [n_p=5.93/λ², f_p^max=0.3f₀]. An analytical argument [16], sketched here, predicts a similar ρ for all samples since the distribution is generated only by pinned vortices and is not affected by the presence of easy-flow channels. The addition of a vortex to the sample exerts a small additional force f on an arbitrary vortex located a small distance r away (r << λ), displacing this vortex a distance

δu(r)=(f/η) δt ∼ K₁(r/λ) ∼ 1/r.

(12)

Since there are

δN(r)=2πr n_v δr

(13)

vortices a distance r from the added vortex, we find

ρ = −d lnδN / d lnδu=−(1/r)(−1/r)⁻¹=1,

(14)

in general agreement with our computed values of ρ,

ρ ≈ 0.9 - 1.4.

(15)

6. Number of vortices leaving the sample

Altering the pinning parameters affects the number of vortices N_f that exit the sample during an avalanche, as shown in the plot of P(N_f) in the inset of Fig. 2a. If we approximate P(N_f) for low N_f by the form

P(N_f) ∼ N_f^−α,

(16)

we find that all samples with high pinning density, n_p=5.93/λ², have α ∼ 2.4. As n_p decreases, α increases: α ∼ 3.4 for n_p=2.40/λ² and α ∼ 4.4 for n_p=0.96/λ². When all vortex motion occurs in an easy-flow interstitial channel, α increases since the channel does not build up enough stress to allow events with large N_f to occur. Smaller events continually relieve the accumulated stress instead. For example, with the small number of flux paths in samples with n_p=0.96/λ², as in Fig. 1a, events with large N_f are rare, and α ∼ 4.4. In samples with high pin density, even after the stress in one vortex path has been depleted by a large avalanche, other areas still contain enough stress to remain active in large and small events while the depleted regions build up stress again. This leads to a greater likelihood of large events and correspondingly smaller values of α, α <~2.4.

7. Relation to experiment

Distributions similar to this high pin density case have been obtained experimentally in [7], where values of α ranging from

α_exp⁽¹⁾ ∼ 1.4 to 2.2

(17)

are observed. The pinning density from grain boundaries in the experimental sample is very high, n_p ∼ 100/λ², so it is reasonable that the α values observed in [7] are similar to the α values produced by our most densely pinned samples. Broad distributions with

α_exp⁽²⁾ ∼ 1.7 to 2.2

(18)

were also observed in [12], in good agreement with both [7] and our results. In addition, [12] finds a regime where avalanches of a characteristic size occur, offering an experimental example in which samples with a lower density of weaker pinning sites produce narrower distributions, as we also observe.

8. Voltage noise power

Voltage noise power can be used to probe the interesting peak effect that appears as an increase in the critical current with increasing applied magnetic field. The resulting increase in noise power has been postulated to result from plastic motion of the vortex lattice [13]. We compare our simulation to experiment by using the analog of an experimentally measured voltage signal, the average vortex velocity

v_av=

N_v

N_v
∑
i=1

v_i .

(19)

Our raw signal v_av, seen in fig. 2 of Ref. [16], strongly resembles experimentally observed voltages, as in fig. 1 of Ref. [7]. To find the power spectra, we measure time in units of the average time of flight t_f of a single vortex across the sample. Such units make it possible to compare our work to experiments in which the time of flight is known. For example, in Ref. [26] vortices travelled 0.22 mm in about 7.2 ms. Taking λ for YBCO to be λ=140 nm, the vortices in our simulation travel the equivalent of 0.0036 mm, and if they are considered to move at the same speed as the vortices of Ref. [26], the time of flight becomes t_f ≈ 1.3 ms. In these units, the spectra shown here range from 300 Hz to 3 MHz in frequency, so the lower part of the frequency range may be compared with experiments.

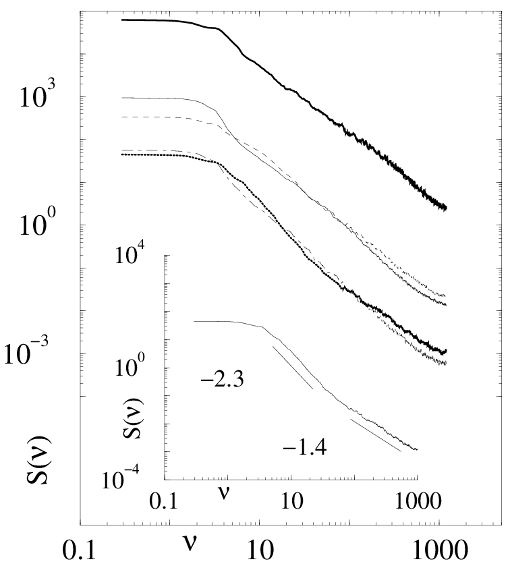Fig. 3: Voltage noise spectrum from each type of sample, with frequencies measured in units of the inverse of the time of flight 1/t_f. Heavy solid line, f_p^max=3.0f₀, n_p=5.93/λ²; solid line, f_p^max=1.0f₀, n_p=5.93/λ²; dashed line, f_p^max=3.0f₀, n_p=2.40/λ²; dot-dashed line, f_p^max=0.3f₀, n_p=5.93/λ²; heavy dotted line, f_p^max=3.0f₀, n_p=0.96/λ²; Each power spectrum was obtained from time series totalling 10⁶ MD steps per sample. Inset: the spectrum of the voltage signal for a sample with high pinning strength f_p^max=3.0f₀ and low pinning density n_p=0.96/λ² has more than one slope.

From the power spectra of v_av for each of our samples, shown in Fig. 3, it is clear that our simulated plastically moving vortex lattice produces broad-band noise that changes in form in a manner consistent with experiment [7,8]. The overall noise power in the simulations is reduced both as the pinning density is reduced and as the pinning strength is lowered. For frequencies ν ≤ 10^-3, the spectrum is flat, indicating that avalanches separated by times ≥ 10³ MD steps are uncorrelated. For ν ≥ 10^-3, samples with a high density of pinning sites produce spectra of the form

v_av=

S(f) ∼ ν^−β, .

(20)

where β increases as the pinning strength decreases: β=1.54 for f_p^max=3.0f₀, β=1.66 for f_p^max=1.0f₀, and β=1.93 for f_p^max=0.3f₀. Since samples with stronger pinning effectively have a lower driving rate than samples with weaker pinning, the change in slope appears consistent with Ref. [7], where the slope increased from β_exp⁽¹⁾ ∼ 1.5 to 2.0 as the driving rate increased. The exponents observed here are also similar to those found by Marley et al. [13], who obtained exponents β_exp⁽²⁾ ∼ 1.5 to 2.0 in the peak effect region near depinning where plastic flow should be occurring.

The linear form of the spectra breaks down in samples with a lower density of pinning sites, which have more correlated vortex motion due to the presence of interstitial channels with typical avalanche lifetimes τ(10²≤ν≤10^-2). This tends to produce a steeper slope in the power spectrum at low frequencies (10^-3≤ν≤10^-2). This is shown in the inset of Fig. 3, where the spectra of these samples have a region of relatively steep slope at lower frequencies and a region with a more gentle slope at higher frequencies.

9. Conclusions

We have quantitatively shown how pinning determines the nature of vortex avalanches. By using large-scale MD simulations, we observe pulses of motion in chain-like disturbances through the sample. The presence or absence of distinct channels for flow leads to a crossover from broad distributions of avalanche size to characteristic sizes. Pinning strength causes a transition between strongly plastic flow to mildly plastic, 'semi-elastic' flow. Lowering the pinning density causes the very broad avalanche distributions to develop characteristic sizes, as well as changing the nature of the voltage noise spectrum.

Acknowledgements

Computer services were provided by: the Maui High Performance Computing Center, sponsored in part by the Phillips Laboratory, Air Force Materiel Command, USAF, under cooperative agreement number F29601-93-2-0001; and by the University of Michigan Center for Parallel Computing, partially funded by NSF grant CDA-92-14296. CO was supported by the NASA Graduate Student Researchers Program.

References

f: Permanent address.
[1]: G.A. Held et al., Phys. Rev. Lett. 65 (1990) 1120.
[2]: M. Bretz et al., Phys. Rev. Lett. 69 (1992) 2431.
[3]: H.M. Jaeger, S.R. Nagel, R.P. Behringer, Rev. Mod. Phys. 68 (1996) 1259, and references therein.
[4]: K.L. Babcock, R.M. Westervelt, Phys. Rev. Lett. 64 (1990) 2168.
[5]: B. Plourde, F. Nori, M. Bretz, Phys. Rev. Lett. 71 (1993) 2749.
[6]: O. Narayan, D.S. Fisher, Phys. Rev. B 49 (1994) 9469.
[7]: S. Field et al., Phys. Rev. Lett. 74 (1995) 1206.
[8]: R.J. Zieve et al., Phys. Rev. B 53 (1996) 11849.
[9]: O. Pla, F. Nori, Phys. Rev. Lett. 67 (1991) 919.
[10]: T. Matsuda et al., Science 271 (1996) 1393.
[11]: F. Nori, Science 271 (1996) 1373.
[12]: E.R. Nowak et al., Phys. Rev. B 55 (1997) 11702.
[13]: A.C. Marley et al., Phys. Rev. Lett. 74 (1995) 3029.
[14]: P. Bak, C. Tang, K. Wiesenfeld, Phys. Rev. A 38 (1988) 364.
[15]: C.P. Bean, Rev. Mod. Phys. 36 (1964) 31.
[16]: C.J. Olson et al., Phys. Rev. B 56, in press, available in Ref. [20].
[17]: C. Reichhardt et al., Phys. Rev. B 52 (1995) 10441.
[18]: C. Reichhardt et al., Phys. Rev. B 53 (1996) R8898.
[19]: C. Reichhardt et al., Phys. Rev. B 54 (1996) 16108.
[20]: Brief vortex avalanche videos are available at
http://www-personal.engin.umich.edu/~nori
[21]: R.D. Merithew et al., Phys. Rev. Lett. 77 (1996) 3197.
[22]: M.C. Faleski, M.C. Marchetti, A.A. Middleton, Phys. Rev. B 54 (1996) 12427.
[23]: H.J. Jensen et al., Phys. Rev. B 38 (1998) 9235.
[24]: A.E. Koshelev, V.M. Vinokur, Phys. Rev. Lett. 73 (1994) 3580.
[25]: N. Gronbech-Jensen, A.R. Bishop, D. Dominguez, Phys. Rev. Lett. 76 (1996) 2985.
[26]: G. D'Anna et al., Phys. Rev. Lett. 75 (1995) 3521.

File translated from T_EX by T_THgold, version 4.00.
Back to Home