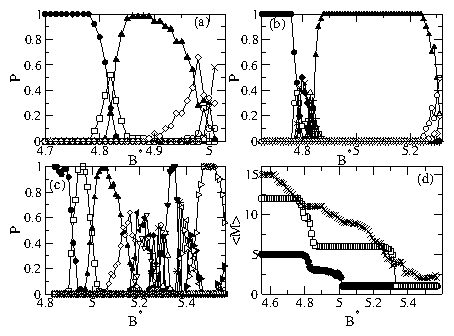
 Figure 4: (a) Decay modes for N=5. P is the probability of observing
the mode, and B* is the quench depth.
•: (15);
square: (13,21);
black triangle: (11,22);
◊: (21,31);
big circle: (12,31);
×: (11,41).
(b) Decay modes for N=12.
•: (112);
square: (111,21);
×: (110,22);
black lozenge: (16,23);
triangle up: (22,31,51);
+: (14,21,32);
black square: (15,22,31);
black triangle: (13,33);
big circle: (12,32,41);
◊: (11,31,42).
(c) Major decay modes for N=15.
•: (17,24);
square: (16,23,31);
black triangle: (15,22,32);
◊: (14,21,33);
black triangle left: (13,21,32,41);
big triangle down: (12,33,41);
+: (12,21,32,51);
black lozenge: (11,33,51);
×: (21,31,52);
big circle: (11,31,51,61);
black square: (12,21,51,61);
big triangle up: (31,51,71);
black triangle down: (11,21,51,71);
∗: (12,61,71);
triangle left: (11,72);
black triangle right: (21,61,71);
triangle right: (71,81).
(d) Average multiplicity 〈M〉 of the decay as a function of
B* for N=5
(•),
12 (square),
and 15
(×).
Figure 4: (a) Decay modes for N=5. P is the probability of observing
the mode, and B* is the quench depth.
•: (15);
square: (13,21);
black triangle: (11,22);
◊: (21,31);
big circle: (12,31);
×: (11,41).
(b) Decay modes for N=12.
•: (112);
square: (111,21);
×: (110,22);
black lozenge: (16,23);
triangle up: (22,31,51);
+: (14,21,32);
black square: (15,22,31);
black triangle: (13,33);
big circle: (12,32,41);
◊: (11,31,42).
(c) Major decay modes for N=15.
•: (17,24);
square: (16,23,31);
black triangle: (15,22,32);
◊: (14,21,33);
black triangle left: (13,21,32,41);
big triangle down: (12,33,41);
+: (12,21,32,51);
black lozenge: (11,33,51);
×: (21,31,52);
big circle: (11,31,51,61);
black square: (12,21,51,61);
big triangle up: (31,51,71);
black triangle down: (11,21,51,71);
∗: (12,61,71);
triangle left: (11,72);
black triangle right: (21,61,71);
triangle right: (71,81).
(d) Average multiplicity 〈M〉 of the decay as a function of
B* for N=5
(•),
12 (square),
and 15
(×).
|