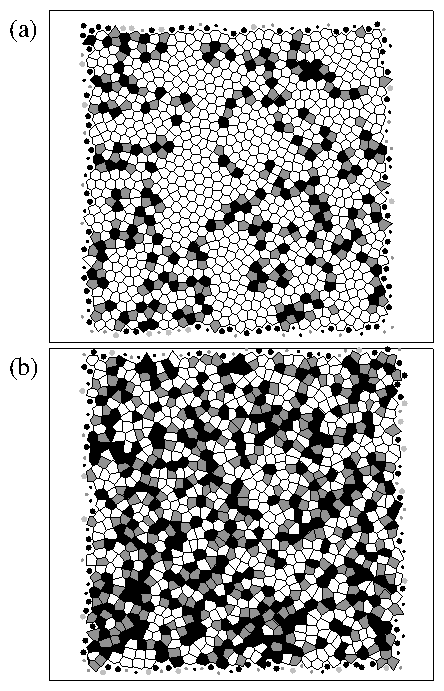
 Figure 1:
The Voronoi constructions for a 2D system of particles interacting
with a screened Coulomb potential. A particle is centered at each polygon
and the polygon color is: nc=6, white; nc=5, dark gray,
nc=7, black. (a)
T/Td = 1.04; (b) T/Td = 7.0.
Figure 1:
The Voronoi constructions for a 2D system of particles interacting
with a screened Coulomb potential. A particle is centered at each polygon
and the polygon color is: nc=6, white; nc=5, dark gray,
nc=7, black. (a)
T/Td = 1.04; (b) T/Td = 7.0.
|


