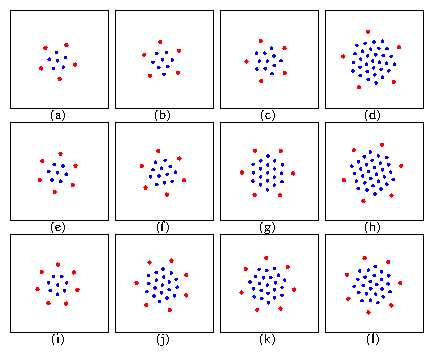
|
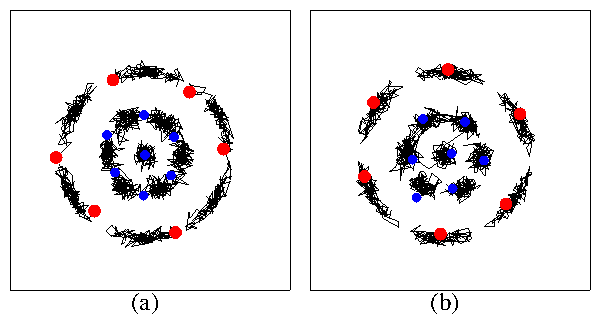
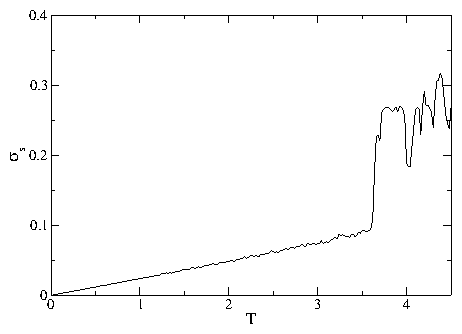
|
| (2) |
| (3) |
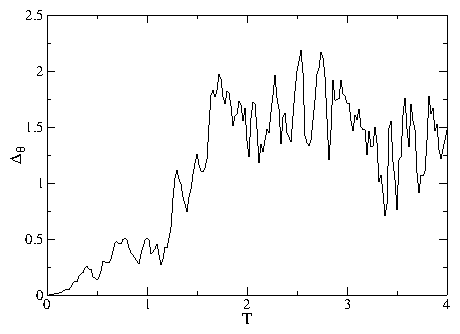
|
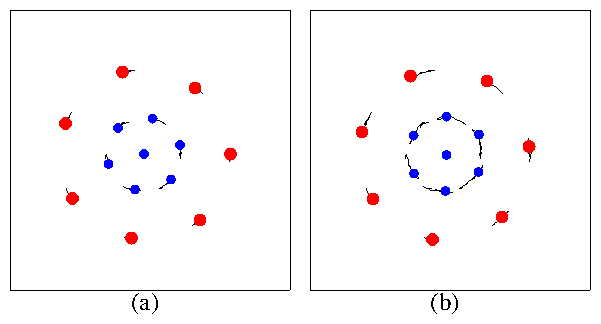
|
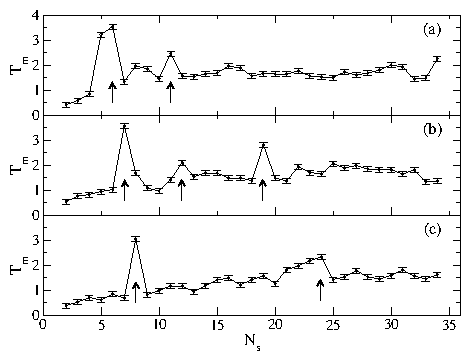 |
References
- [1]
- M.A. Reed and W.P. Kirk, Nanostructure Physics and Fabrication (Academic Press: Boston, 1989).
- [2]
- P. Leiderer, W. Ebner, and V.B. Shilkin, Surf. Sci. 113, 105 (1987).
- [3]
- Y. Kondo, J.S. Korhonen, M. Krusius, V.V. Dmitriev, E.V. Thuneberg, and G.E. Volovik, Phys. Rev. Lett. 68, 3331 (1992).
- [4]
- R. Bubeck, C. Bechinger, S. Neser, and P. Leiderer, Phys. Rev. Lett. 82, 3364 (1999).
- [5]
- M. Golosovsky, Y. Saado, and D. Davidov, Phys. Rev. E 65, 061405 (2002).
- [6]
- W-T. Juan, Z-H. Huang, J-W. Hsu, Y-J. Lai, and Lin I, Phys. Rev. E 58, R6947 (1998).
- [7]
- J.J. Thomson, Philos. Mag. 7, 237 (1904); B. Partoens and F.M. Peeters, J. Phys.: Condens. Matter 9, 5383 (1997).
- [8]
- V.M. Bedanov and F.M. Peeters, Phys. Rev. B 49, 2667 (1994).
- [9]
- V.A. Schweigert and F.M. Peeters, Phys. Rev. B 51, 7700 (1995).
- [10]
- A.A. Koulakov and B.I. Shklovskii, Phys. Rev. B 57, 2352 (1998).
- [11]
- I.V. Schweigert, V.A. Schweigert, and F.M. Peeters, Phys. Rev. Lett. 84, 4381 (2000).
- [12]
- Y-J. Lai and Lin I, Phys. Rev. E 64, 015601 (2001).
- [13]
- Q.-H. Wei, C. Bechinger, D. Rudhardt, and P. Leiderer, Phys. Rev. Lett. 81, 2606 (1998).
- [14]
- M. Kong, B. Partoens, and F.M. Peeters, Phys. Rev. E 65, 046602 (2002).
- [15]
- All configurations can be seen at http://www.t12.lanl.gov/home/olson/Colloid2S.html.
File translated from TEX by TTHgold, version 4.00.
Back to Home