New Journal of Physics 17, 073034 (2015)

Magnus-induced ratchet effects for skyrmions interacting with asymmetric substrates

C. Reichhardt, D. Ray, and C. J. Olson Reichhardt

Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

Keywords: skyrmion, ratchet, substrate
Received 20 May 2015
Revised 30 June 2015
Accepted for publication 6 July 2015
Published 31 July 2015
Abstract
We show using numerical simulations that pronounced ratchet effects can occur for ac driven skyrmions moving over asymmetric quasi-one-dimensional substrates. We find a new type of ratchet effect called a Magnus-induced transverse ratchet that arises when the ac driving force is applied perpendicular rather than parallel to the asymmetry direction of the substrate. This transverse ratchet effect only occurs when the Magnus term is finite, and the threshold ac amplitude needed to induce it decreases as the Magnus term becomes more prominent. Ratcheting skyrmions follow ordered orbits in which the net displacement parallel to the substrate asymmetry direction is quantized. Skyrmion ratchets represent a new ac current-based method for controlling skyrmion positions and motion for spintronic applications.
1. Introduction
2. Results and discussion
2.1. ac driving parallel to substrate asymmetry
2.2. ac driving perpendicular to substrate asymmetry
2.3. Frequency dependence
2.4. Discussion
3. Summary
References

1.  Introduction

Ratchet effects can arise when particles placed in an asymmetric environment are subjected to suitable nonequilibrium conditions such as an externally applied ac drive, which produces a net dc motion of the particles [1]. Ratchet effects have been realized for colloidal systems [2], cold atoms in optical traps [3], granular media on sawtooth substrates [4], and the motion of cells crawling on patterned asymmetric substrates[5], and they can be exploited to create devices such as shift registers for domain walls moving in an asymmetric substrate [6]. There has been intense study of ratchet effects for magnetic flux vortices in type-II superconductors interacting with quasi-one-dimensional (q1D) or two-dimensional (2D) asymmetric pinning substrates. The vortices can be effectively described as overdamped particles moving over an asymmetric substrate, and under ratcheting conditions the application of an ac driving current produces a net dc flux flow [7,8,9,10,11,12]. The simplest vortex ratchet geometry was first proposed by Lee et al. [7], where an effectively 2D assembly of vortices was driven over a q1D asymmetrically modulated substrate using an ac driving force oriented along the direction of the substrate asymmetry.
Skyrmions in chiral magnets, initially discovered in MnSi [13] and subsequently identified in numerous other materials at low [14,15,16,17] and room temperatures [18,19,20,21,22], have many similarities to superconducting vortices. Skyrmions are spin textures forming topologically stable particle-like objects [17] that can be set into motion by the application of a spin-polarized current [23,24,25,26,27]. As a function of the external driving, skyrmions can exhibit a depinning transition similar to that found for vortices, and from transport measurements it is possible to construct skyrmion velocity versus applied force curves [24,26,27,28,29,30]. It has been shown that the dynamics of skyrmions interacting with pinning can be captured by an effective particle equation of motion, which produces pinning-depinning and transport properties that agree with those obtained using a continuum-based model [28], just as a particle-based description for vortices can effectively capture the vortex dynamics in the presence of pinning sites [31]. Due to their size scale and the low currents required to move them, skyrmions show tremendous promise for applications in spintronics such as race-track type memory devices [32,33] originally proposed for domain walls [34], and it may be possible to create skyrmion logic devices similar to those that harness magnetic domain walls [35]. In order to realize such skyrmion applications, new methods must be developed to precisely control skyrmion positions and motion.
The most straightforward approach to a skyrmion ratchet is to utilize the same types of asymmetric substrates known to produce ratchet effects in vortex systems. There are, however, important differences between skyrmion and vortex dynamics due to the strong non-dissipative Magnus component of skyrmion motion [13,17,24,26,28,29] that is absent in the vortex system. The Magnus term produces a skyrmion velocity contribution that is perpendicular to the direction of an applied external force. In the presence of pinning, the Magnus term reduces the effectiveness of the pinning by causing the skyrmions to deflect around the edges of attractive pinning sites [26,28,29] rather than being captured by the pinning sites as overdamped vortices are. The Magnus term also produces complex winding orbits for skyrmions moving in confined regions [36] or through pinning sites [26,28,29,37,38,39]. The ratio of the strength of the Magnus term αm to the dissipative term αd can be 10 or higher for skyrmion systems [17]. In contrast, although it is possible for a Magnus effect to appear for vortices in superconductors, it is generally very weak so that the vortex dynamics is dominated by dissipation [31]. A key question is how the Magnus force could impact possible ratchet effects for skyrmions, and whether new types of ratchet phenomena can be realized for skyrmion systems that are not accessible in overdamped systems [40].
Fig1.png
Figure 1: A schematic of the sample geometry where a skyrmion is placed on a q1D asymmetric periodic substrate. An ac driving force Faccos(ωt) is applied parallel (Fac||) or perpendicular (Fac⊥) to the substrate asymmetry direction.
In this work we numerically examine a 2D assembly of skyrmions interacting with a q1D asymmetric periodic substrate shown schematically in figure 1. An ac drive is applied either parallel (Fac||) or perpendicular (Fac⊥) to the substrate asymmetry direction, which runs along the x axis. In the overdamped limit, no ratchet effect appears for Fac⊥; however, we find that the Magnus effect produces a novel ratchet effect for Fac⊥ when it curves the skyrmion trajectories into the asymmetry or x direction. We model the skyrmion dynamics in a sample with periodic boundary conditions using a particle based description [28,39] and vary the ratio of the Magnus to dissipative dynamic terms, the amplitude and frequency of the ac drive, and the strength of the substrate.
Simulation- The equation of motion for a single skyrmion with velocity v moving in the x−y plane is
αdv + αm
^
z
 
 ×v = FSP + Fac||,⊥
(1)
The damping term αd keeps the skyrmion velocity aligned with the direction of the net external force, while the Magnus term αm rotates the velocity toward the direction perpendicular to the net external forces. To examine the role of the Magnus term we vary the relative strength αm/αd of the Magnus term to the dissipative term under the constraint α2d + α2m = 1, which maintains a constant magnitude of the skyrmion velocity. The substrate force FSP = −∇U(x) ∧x arises from a ratchet potential
U(x) = U0[sin(2πx/a) + 0.25sin(4πx/a)],
(2)
where a is the periodicity of the substrate and we define the strength of the substrate to be Ap = 2πU0/a. The ac driving term is either Fac|| = Fac||cos(ωt)∧x or Fac⊥ = Fac⊥cos(ωt)∧y. We measure the time-averaged skyrmion velocities parallel 〈V〉|| ≡ 2π〈v ·∧x 〉/ωa or perpendicular 〈V〉⊥ ≡ 2π〈v ·∧y 〉/ωa to the substrate asymmetry direction as we vary the ac amplitude, substrate strength, or ω. Here we focus primarily on samples with Ap = 1.5 and ω = 2.5×10−6 inverse simulation time steps, and we consider the sparse limit of a single skyrmion which can also apply to regimes in which skyrmion-skyrmion interactions are negligible.

2.  Results and discussion

Fig2.png
Figure 2: The skyrmion velocity parallel 〈V〉|| (red) and perpendicular 〈V〉⊥ (blue) to the substrate asymmetry vs Fac|| for a substrate strength of Ap = 1.5. (a) At αm/αd = 0.0, the overdamped limit, only 〈V〉|| is nonzero and shows quantized steps with 〈V〉|| = n, where n is an integer. (b) At αm/αd = 1.6, there is quantized motion in both the parallel and perpendicular directions. (c) αm/αd = 4.58. (d) αm/αd = 7.85. The points labeled B and C indicate where the skyrmion orbits in figure 3(b,c) were obtained.

2.1.  ac driving parallel to substrate asymmetry

We first apply the ac driving force parallel to the asymmetry direction, a configuration previously studied for the same type of substrate in vortex systems [7,12]. In figure 2 we plot 〈V〉|| and 〈V〉⊥ versus Fac|| for samples with Ap = 1.5, so that the maximum magnitude of the substrate force is Fsmax=2.0 in the negative x direction and Fsmax=1.0 in the positive x direction. The overdamped limit αm/αd = 0.0 appears in figure 2(a), where 〈V〉⊥ = 0.0 and there is a ratchet effect only along the parallel or x-direction for Fac|| > 1.25. The skyrmion velocity is quantized and forms a series of steps with 〈V〉|| = n where n is an integer. On the highest step in figure 2(a) near Fac||=2.3, n = 7. The quantization indicates that during one ac driving period, the skyrmion moves a net distance of na in the parallel direction. For very large values of Fac||, the velocity quantization is lost and the parallel ratchet effect gradually diminishes. In figure 2(b) we plot 〈V〉|| and 〈V〉⊥ for a sample with αm/αd = 1.6, showing a nonzero skyrmion velocity component for both the parallel and perpendicular directions. There is again a quantization of the parallel velocity 〈V〉||, and the Magnus term transfers this quantization into the perpendicular direction even though there is no periodicity of the substrate along the y direction. Thus, we find 〈V〉⊥=nαm/αd. For Fac|| > 5.0, we find windows in which the ratcheting effect is lost and 〈V〉||=〈V〉⊥=0. As αm/αd increases, the maximum value of n decreases, so that at αm/αd = 4.58 in figure 2(c), only the n = 1 step appears. At the same time, the width of the non-ratcheting windows increases, as shown in figure 2(d) for αm/αd = 7.858. These results show that while a ratchet effect does occur for skyrmion systems, an increase in the Magnus term decreases the range of ac drives over which the ratchet effect can be observed.
Fig3.png
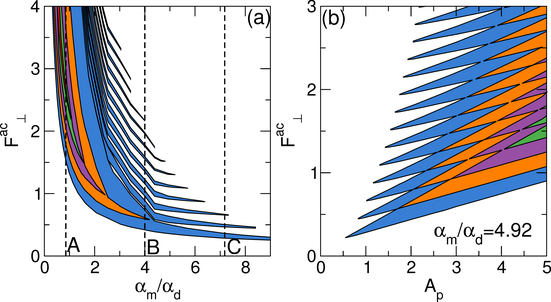
Figure 3: (a) A plot of Fac|| vs αm/αd indicating all n=1 (blue) ratcheting regions, and the inner envelopes of the n=2 (orange), 3 (purple), 4 (green), 5 (red) and 6 (yellow) ratcheting regions. The boundaries of the inner envelopes are defined as the point at which the ratchet velocity first reaches the value n followed by the point at which it first drops below n. The y-axis marked A and the dashed lines marked B−D are the values of αm/αd for which the velocity curves in figure 2 were obtained. The minimum ac amplitude required to produce a ratchet effect increases with increasing αm/αd. (b,c) Skyrmion trajectory images. White (green) regions are high (low) areas of the substrate potential. Thin black lines indicate forward motion of the skyrmion and thick purple lines indicate backward motion. The red circle is the skyrmion. (b) The n = 3 orbit at αm/αd = 1.6 for Fac|| = 2.2 from figure 2(b). The skyrmion moves in straight lines and translates 3a in the x direction during one ac drive cycle. (c) The n = 1 orbit at αm/αd = 4.58 for Fac|| = 2.0 from figure 2(c), where the skyrmion translates a distance a in the x direction during every ac drive cycle.
By lowering the ac frequency ω or increasing the substrate strength Ap, it is possible to increase the range and magnitude of the skyrmion ratchet effect. In figure 3(b,c) we show representative skyrmion orbits for the system in figure 2(b,c). Figure 3(b) shows the orbits at αm/αd = 1.6 for Fac|| = 2.2, corresponding to the n = 3 step in figure 2(b). Here the skyrmion moves along straight lines oriented at an angle to the direction of the applied ac drive. During each ac cycle, the skyrmion first translates a distance 3a in the positive x direction and then travels in the reverse direction for a distance of a/2 before striking the top of the potential barrier, which it cannot overcome in the reverse x direction for this magnitude of ac drive. It repeats this motion in each cycle. In figure 3(c) we show the skyrmion orbit at αm/αd = 4.58 for Fac|| = 2.0, corresponding to the n = 1 orbit in figure 2(c). The angle the skyrmion motion makes with the ac driving direction is much steeper, and the skyrmion is displaced a net distance of a in the x direction during each ac driving cycle.
In order to clarify the evolution of the ratchet phases as a function of αm/αd and Fac||, in figure 3(a) we plot the ratchet envelopes for the n=1 to n=6 steps. For the n=1 case we show, in blue, all of the regions in the Fac|| − αm/αd plane where n=1 steps appear. For n=2 to n=6, to prevent overcrowding of the graph, instead of plotting all ratchet regions we show only the inner step envelope for each n=ni, obtained from simulations in which Fac|| is swept up from zero, and defined to extend from the drive at which n first reaches ni to the drive at which n first drops below ni. We find that the minimum Fac|| required to induce a ratchet effect increases linearly with increasing αm/αd, and that the ratcheting regions form a series of tongue features (shown for n=1 only). The ratchet effects persist up to and beyond αm/αd = 10. For αm/αd = 0, the strongest ratchet effects with the largest values of n occur near Fac|| = 2.3, corresponding to a driving force that is slightly higher than the maximum force exerted on the skyrmion by the substrate when it is moving with a negative x velocity component. As Fac|| increases above this value, the skyrmion can slip backward over more than one substrate plaquette during each ac cycle, limiting its net forward progress.
Fig4.png
Figure 4: The skyrmion velocity parallel 〈V〉|| (red) and perpendicular 〈V〉⊥ (blue) to the substrate asymmetry vs Fac⊥ for samples with Ap = 1.5. (a) At αm/αd = 0.855, ratcheting occurs in both the parallel and perpendicular directions for Fac⊥ > 1.5, and 〈V〉|| = n with integer n. Inset: At αm/αd = 0, there is no ratchet effect. (b) αm/αd = 4.0. (c) αm/αd = 7.018. Inset: A blowup of 〈V〉|| from the main panel at the third n=1 step showing that additional fractional steps appear at velocity values such as n/m = 1/2.

2.2.  ac driving perpendicular to substrate asymmetry

In figure 4 we plot 〈V〉|| and 〈V〉⊥ versus Fac⊥ for Ap = 1.5. The inset in figure 4(a) shows that for αm/αd = 0, 〈V〉|| = 〈V〉⊥ = 0, indicating that there is no ratchet effect in either direction. When the Magnus term is finite, as in figure 4(a) where αm/αd = 0.855, pronounced ratcheting occurs in both the parallel and perpendicular directions. We describe this as a Magnus-induced transverse ratchet effect. Here 〈V〉|| is quantized at integer values, with the largest step in figure 4(a) falling at n=5, and 〈V〉⊥/〈V〉|| = αm/αd. As αm/αd increases, figure 4(b,c) shows that the maximum value of Fac⊥ at which ratcheting occurs decreases, as does the maximum value of n and the widths of the ratcheting windows. In addition to the integer steps in 〈V〉||, we also observe fractional steps, as shown in the inset of figure 4(c) for αm/αd=7.018, where we highlight the third n = 1 step. On the upper n=1 step edge there is a plateau at 〈V〉|| = 1/2 and additional steps at 〈V〉||=3/4, 2/3, 1/3, and 1/4, which are accompanied by even smaller steps that form a devil's staircase structure [41]. For higher values of Fac⊥, smaller plateaus appear at rational fractional velocity values 〈V〉||=n/m with integer n and m, while full locking to the integer n = 1 step no longer occurs. The n/m rational locking steps also occur for parallel ac driving but are much weaker than for perpendicular ac driving.
Fig5.png
Figure 5: Skyrmion trajectory images from the system in figure 4. White (green) regions are high (low) areas of the substrate potential. Black lines indicate the motion of the skyrmion; the red circle is the skyrmion. (a) The n = 2 step at αm/αd = 0.855 for Fac⊥ = 2.0. (b) The n = 1 step at αm/αd = 4.0 for Fac⊥ = 0.7. (c) A non-ratcheting orbit at αm/αd = 4.0 for Fac⊥ = 0.76. (d) For higher ac drives the orbits become more complicated, as shown here for αm/αd = 4.0 at Fac⊥ = 1.97.
The skyrmion orbits for perpendicular ac driving differ markedly from those that appear under parallel ac driving, since the Magnus term induces a velocity component perpendicular to the direction of the external driving force. As a result, perpendicular ac drives induce parallel skyrmion motion that interacts with the substrate asymmetry. Figure 5(a) shows a skyrmion orbit on the 〈V〉|| = 2 step for Fac⊥ = 2.0 and αm/αd = 0.855 from figure 4(a). The skyrmion no longer moves in straight lines, as it did for the parallel ac drive in figure 3. Instead it follows a complicated 2D trajectory, translating a net distance of 2a in the x direction during every ac drive cycle. In figure 5(b) we plot an n = 1 orbit at Fac⊥ = 0.7 for αm/αd = 4.0 from figure 4(b), where there is a similar orbit structure in which the skyrmion translates a net distance of a in the x direction in each ac drive cycle. Figure 5(c) shows a non-ratcheting orbit for αm/αd = 4.0 at Fac⊥ = 0.75, where the skyrmion traces out a complicated periodic closed cycle. For higher ac amplitudes, the ratcheting orbits become increasingly intricate, as shown in figure 5(d) for αm/αd = 4.0 at Fac⊥ = 1.97.
Fig6.png
Figure 6: (a) A plot of Fac⊥ vs αm/αd indicating all n=1 (blue) ratcheting regions, and the inner envelopes of the n=2 (orange), 3 (purple), 4 (green), and 5 (red) ratcheting regions. The dashed lines marked A−C are the values of αm/αd for which the velocity curves in figure 4 were obtained. There is no ratchet effect at the overdamped limit of αm/αd = 0, and the minimum ac amplitude required to produce a ratchet effect decreases with increasing αm/αd. (b) A plot of Fac⊥ vs Ap for αm/αd = 4.92 indicating the ratcheting regions with n=1 (blue), 2 (orange), 3 (purple), and 4 (green). As the substrate strength increases, stronger ratchet effects appear.
In figure 6(a) we show the full n=1 ratchet regions and the inner envelopes of the n=2 to 5 ratchet regions as a function of Fac⊥ and αm/αd. For low values of αm/αd, there is no ratcheting since the Magnus term is too weak to bend the skyrmion trajectories far enough to run along the direction parallel to the asymmetry. The minimum ac amplitude required to generate a ratchet effect decreases as the strength of the Magnus term increases, opposite to what we found for parallel ac driving in figure 3(a). Here, the skyrmion trajectories are more strongly curved into the parallel direction as αm/αd increases, so that a lower ac amplitude is needed to push the skyrmions over the substrate potential barriers. In contrast, for a parallel ac drive the Magnus term curves the skyrmion trajectories out of the parallel direction, so that a larger ac amplitude must be applied for the skyrmions to hop over the substrate maxima. We also find that as αm/αd increases, the minimum ac force needed to produce a ratchet effect drops below the pinning force exerted by the substrate. This cannot occur in overdamped systems, and is an indication that the Magnus term induces some inertia-like behavior. The threshold ac force value Fth for ratcheting to occur can be fit to Fth⊥ ∝ (αm/αd)−1 for perpendicular driving, while for parallel driving, Fth|| ∝ αm/αd. As αm/αd increases, the extent of the regions where ratcheting occurs decreases; however, by increasing the substrate strength, the regions of ratcheting broaden in extent and the magnitude of the ratchet effect increases. In figure 6(b) we show the evolution of the n = 1, 2, 3 and 4 ratchet regions as a function of Fac⊥ and Ap for fixed αm/αd = 4.92. Here, as Ap increases, the magnitude of the ratchet effect increases, forming a series of tongues. The minimum ac force needed to induce a ratchet effect increases linearly with increasing Ap. We find the same behavior of the ratchet regions when we vary Ap for different parallel drives Fac|| (not shown). These results indicate that skyrmions can exhibit a new type of Magnus-induced ratchet effect that appears when the driving force is applied perpendicular to the asymmetry direction of the substrate.
Fig7.png
Figure 7: The magnitude of 〈V〉|| in samples with Ap = 1.5 and αm/αd = 3.042. (a) As a function of Fac⊥ and ω in units of 10−5 inverse simulation time steps, 〈V〉|| has clear tongue structures, and its magnitude is non-monotonic for varied frequency. (b) 〈V〉|| as a function of Fac|| and ω has similar features.

2.3.  Frequency dependence

In figure 7(a) we plot a heat map of the parallel ratchet velocity 〈V〉|| for perpendicular ac driving as a function of Fac⊥ and ω in a sample with Ap = 1.5 and αm/αd = 3.042. The ratchet effect extends over a wider range of Fac⊥ at low ac driving frequencies, while for higher ω the ratcheting regions form a series of tongues. The ratchet magnitude is non-monotonic as a function of ω, and in several regions it increases in magnitude with increasing ω, such as on the first tongue where the maximum ratcheting effect effect occurs near ω = 10−3 inverse simulation time steps before decreasing again as ω increases further. We find very similar ratchet behaviors for parallel ac driving, as shown in figure 7(b) where we plot 〈V〉|| as a function of Fac|| and ω and observe a series of tongues.

2.4.  Discussion

All of the ratchet effects we describe should be robust against distortions and imperfections in the substrate pattern. The q1D nature of the substrate renders the ratchet behavior relatively insensitive to point-like imperfections of the type that are the most likely to be present in an actual physical realization of the potential. One-dimensional imperfections such as variations in the distance between neighboring substrate minima that are correlated along the entire length of the q1D potential could reduce the magnitude of the ratchet effect, but would not destroy it unless the distortions were severe enough to destroy the periodicity of the substrate. Distortions of this size should be easily preventable and would not be expected to occur in a real sample.
The minimum substrate spacing a for which our ratchet predictions are expected to remain valid is the same as the minimum skyrmion-skyrmion spacing at which the particle-based model breaks down; below this spacing, distortions of the skyrmion shape could affect the ratcheting. In principle there is no maximum spacing a at which our predictions cease to apply since the ratchet mechanism does not require collective skyrmion-skyrmion interactions to be present. The limit of very large a would require large driving forces and/or low ac driving frequencies to produce a ratchet effect.

3.  Summary

Our results show that skyrmions are an ideal system in which to realize ratchet effects in the presence of asymmetric substrates. As expected, they undergo ratcheting when an ac drive is applied parallel to the substrate asymmetry direction; however, the skyrmions also exhibit a unique ratchet feature not found in overdamped systems, which is the transverse ratchet effect. Here, when the ac drive is applied perpendicular to the substrate asymmetry direction, the Magnus term curves the skyrmion orbits and drives them partially parallel to the asymmetry, generating ratchet motion. The asymmetric substrates we consider could be created using methods similar to those employed to create quasi-one-dimensional asymmetric potentials in superconductors and related systems, such as nanofabricated asymmetric thickness modulation, asymmetric regions of radiation damage, asymmetric doping, or blind holes arranged in patterns containing density gradients. Since the skyrmion ratchet effects persist down to low frequencies, it should be possible to directly image the ratcheting motion, while for higher frequencies the existence of ratchet transport can be deduced from transport studies. Such ratchet effects offer a new method for controlling skyrmion motion that could be harnessed in skyrmion applications. We also expect that skyrmions could exhibit a rich variety of other ratchet behaviors under different conditions, such as more complicated substrate geometries, use of asymmetric ac driving, or collective effects due to skyrmion-skyrmion interactions.

  Acknowledgements

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396. DR acknowledges support provided by the Center for Nonlinear Studies.

References

[1]
Reimann P 2002 Phys. Rep. 361 57
[2]
Rousselet J, Salome L, Ajdari A and Prost J 1994 Nature (London) 370 446
[3]
Salger T, Kling S, Hecking T, Geckeler C, Morales-Molina L and Weitz M 2009 Science 326 1241
[4]
Farkas Z, Tegzes P, Vukics A and Vicsek T 1999 Phys. Rev. E 60 7022
[5]
Mahmud G, Campbell C J, Bishop K J M, Komarova Y A, Chaga O, Soh S, Huda S, Kandere-Grzyboswka K and Grzyboswki B A 2009 Nature Phys. 5 606
[6]
Franken J H, Swagten H J M and Koopmans B, Nature Nanotechnol. 7 499
[7]
Lee C S, Jankó B, Derényi I and Barabási A L 1999 Nature (London) 400 337
[8]
Wambaugh J F, Reichhardt C, Olson C J, Marchesoni F and Nori F 1999 Phys. Rev. Lett. 83 5106
[9]
Olson C J, Reichhardt C, Jankó B and Nori F 2001 Phys. Rev. Lett. 87 177002
[10]
Villegas J E, Savel'ev S, Nori F, Gonzalez E M, Anguita J V, García R and Vicent J L 2003 Science 302 1188
[11]
de Souza Silva C C, Van de Vondel J, Morelle M and Moshchalkov V V 2006 Nature (London) 440 651
[12]
Lu Q, Reichhardt C J O and Reichhardt C 2007 Phys. Rev. B 75 054502
[13]
Mülbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R and Böni P 2009 Science 323 915
[14]
Yu X Z, Onose Y, Kanazawa N, Park J H, Han J H, Matsui Y, Nagaosa N and Tokura Y 2010 Nature 465 901
[15]
Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, Bihlmayer G and Blügel S 2011 Nature Phys. 7 713
[16]
Seki S, Yu X Z, Ishiwata S and Tokura Y 2012 Science 336 198
[17]
Nagaosa N and Tokura Y 2013 Nature Nanotechnol. 8 899
[18]
Woo S, Litzius K, Krüger B, Im M-Y, Caretta L, Richter K, Mann M, Krone A, Reeve R, Weigand M, Agrawal P, Fischer P, Kläui M and Beach G S D arXiv:1502.07376 (unpublished)
[19]
Moreau-Luchaire C, Moutafis C, Reyren N, Sampaio J, Van Horne N, Vaz C A F, Bouzehouane K, Garcia K, Deranlot C, Warnicke P, Wohlhüter P, George J M, Raabe J, Cros V and Fert A arXiv:1502.07853 (unpublished)
[20]
Tokunaga Y, Yu X Z, White J S, Rønnow H M, Morikawa D, Taguchi Y and Tokura Y arXiv:1503.05651 (unpublished)
[21]
Chen G, Mascaraque A, N'Diaye A T and Schmid A K 2015 Appl. Phys. Lett. 106, 242404
[22]
Jiang W, Upadhyaya P, Zhang W, Yu G, Jungfleisch M B, Fradin F Y, Pearson J E, Tserkovnyak Y, Wang K L, Heinonen O, te Velthuis S G E and Hoffmann A 2015 Science, in press
[23]
Jonietz F, Mühlbauer S, Pfleiderer C, Neubauer A, Münzer W, Bauer A, Adams T, Georgii R, Böni P, Duine R A, Everschor K, Garst M and Rosch A 2010 Science 330 1648
[24]
Schulz T, Ritz R, Bauer A, Halder M, Wagner M, Franz C, Pfleiderer C, Everschor K, Garst M and Rosch A 2012 Nature Phys. 8 301
[25]
Yu X Z, Kanazawa N, Zhang W Z, Nagai T, Hara T, Kimoto K, Matsui Y, Onose Y and Tokura Y 2012 Nature Commun. 3 988
[26]
Iwasaki J, Mochizuki M and Nagaosa N 2013 Nature Commun. 4 1463
[27]
Lin S-Z, Reichhardt C, Batista C D and Saxena A 2013 Phys. Rev. Lett. 110 207202
[28]
Lin S-Z, Reichhardt C, Batista C D and Saxena A 2013 Phys. Rev. B 87 214419
[29]
Reichhardt C, Ray D and Reichhardt C J O 2015 Phys. Rev. Lett. 114 217202
[30]
Liang D, DeGrave J P, Stolt M J, Tokura Y and Jin S arXiv:1503.03523 (unpublished)
[31]
Brandt E H 1995 Rep. Prog. Phys. 58 1465
[32]
Fert A, Cros V and Sampaio J 2013 Nature Nanotechnol. 8 152
[33]
Sampaio J, Cros V, Rohart S, Thiaville A and Fert A 2013 Nature Nanotechnol. 8 839
[34]
Parkin S S, Hayashi M and Thomas L 2008 Science 320 190
[35]
Allwood D A, Xiong G, Faulkner C C, Atkinson D, Petit D and Cowburn R P 2005 Science 309 1688
[36]
Büttner F, Moutafis C, Schneider M, Krüger B, Günther C M, Geilhufe J, von Korff Schmising C, Mohanty J, Pfau B, Schaffert S, Bisig A, Foerster M, Schulz T, Vaz C A F, Franken J H, Swagten H J M, Kläui M and Eisebitt S 2015 Nature Phys. 11 225
[37]
Liu Y-H and Li Y-Q 2013 J. Phys.: Condens. Matter 25 076005
[38]
Müller J and Rosch A 2015 Phys. Rev. B 91 054410
[39]
Reichhardt C, Ray D and Reichhardt C J O 2015 Phys. Rev. B 91 104426
[40]
A ratcheting motion of skyrmions was discused in Mochizuki M, Yu X Z, Seki S, Kanazawa N, Koshibae W, Zang J, Mostovoy M, Tokura Y and Nagaosa Y 2014 Nature Mater. 13 241; however, this is for a system with no imposed asymmetric substrate and is different from the ratchet effects we study in this work.
[41]
Bak P and Bruinsma R 1982 Phys. Rev. Lett. 49 249


File translated from TEX by TTHgold, version 4.00.
 Back to Home