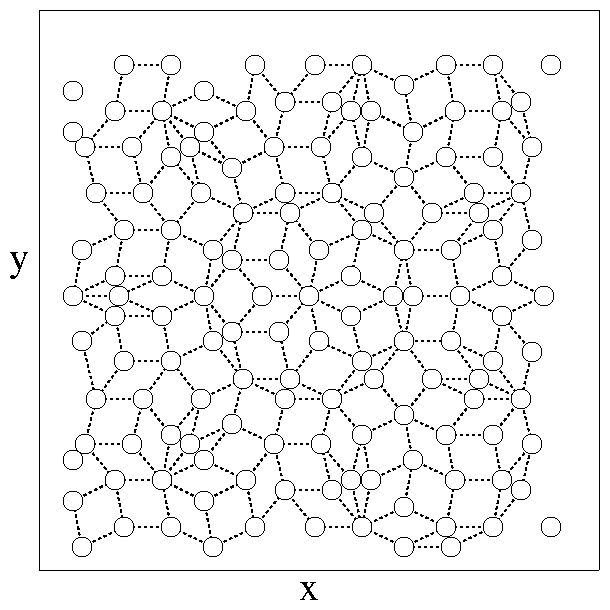
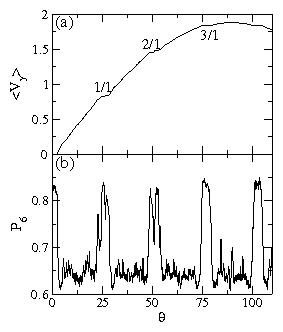
 Figure 2:
(a) The average velocity in the y-direction 〈Vy〉
vs drive angle θ for the system in Suppl. Fig. 1
with a sevenfold quasicrystalline pinning array for
Fp = 1.85, rp = 0.35λ, B/Bϕ = 3.9, and FD=0.2.
Several steps appear at the directional locking angles which are
integer multiples of 360°/14.
The 1/1, 2/1, 3/1, and 4/1 lockings are clearly visible.
(b) The corresponding P6 vs θ
shows that on the locking steps the system develops a considerable
amount of sixfold ordering.
Figure 2:
(a) The average velocity in the y-direction 〈Vy〉
vs drive angle θ for the system in Suppl. Fig. 1
with a sevenfold quasicrystalline pinning array for
Fp = 1.85, rp = 0.35λ, B/Bϕ = 3.9, and FD=0.2.
Several steps appear at the directional locking angles which are
integer multiples of 360°/14.
The 1/1, 2/1, 3/1, and 4/1 lockings are clearly visible.
(b) The corresponding P6 vs θ
shows that on the locking steps the system develops a considerable
amount of sixfold ordering.
|