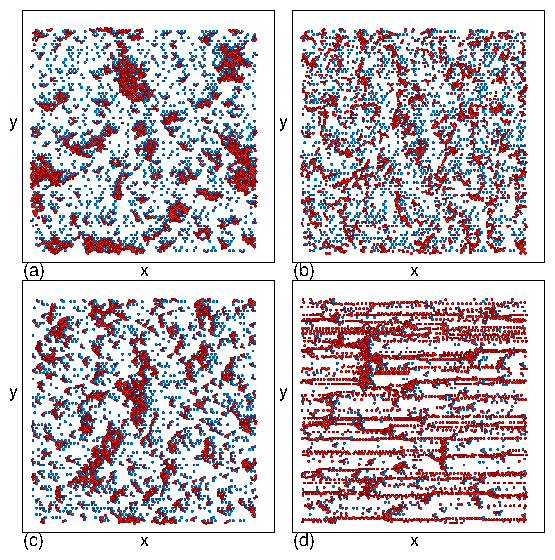
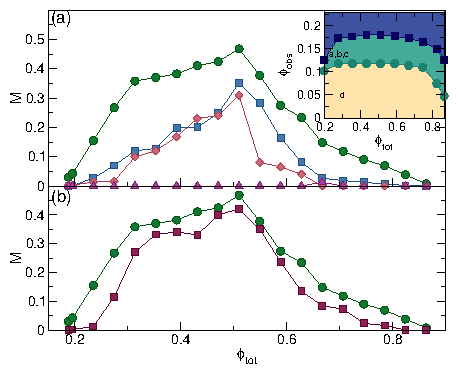
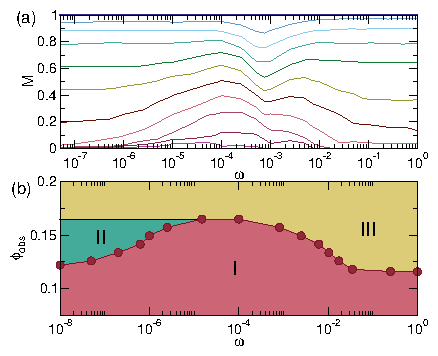
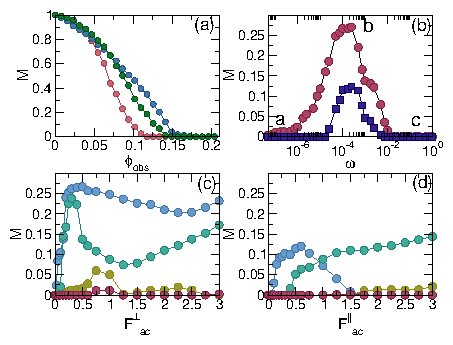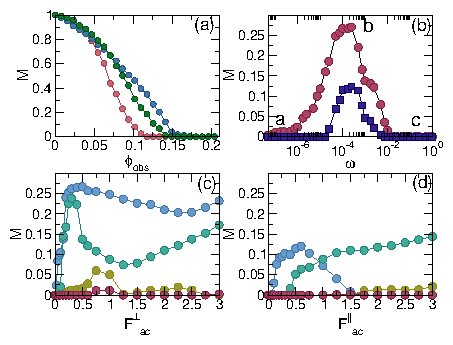 Figure 2: (a) Mobility M vs obstacle density ϕobs
for ϕtot = 0.275 at F⊥ac = F||ac=0 (pink), where
M = 0 for ϕobs > 0.115;
at F⊥ac = 0.5 and ω = 10−4 (blue),
where M ≈ 0 for ϕobs > 0.195;
and at F||ac = 0.5 and ω = 10−4 (green),
where M ≈ 0 for ϕobs > 0.155.
(b) M vs ac frequency ω
for the system in Fig. 1(a-c) at
ϕtot = 0.275, ϕobs = 0.1256, and Fac = 0.5
for transverse (pink circles) and longitudinal (blue squares) ac driving
showing a low frequency clogged state,
an intermediate frequency flowing state, and a high frequency clogged state.
The letters a, b, c mark the frequencies at which the images in Fig. 1(a-c) were
obtained.
(c) M vs F⊥ac for the system in (b)
under transverse driving with ω = 10−4 (blue),
10−3 (green), 10−2 (gold), and 10−1 (red).
(d) M vs Fac|| at the same frequencies as
in (c) under longitudinal driving.
Figure 2: (a) Mobility M vs obstacle density ϕobs
for ϕtot = 0.275 at F⊥ac = F||ac=0 (pink), where
M = 0 for ϕobs > 0.115;
at F⊥ac = 0.5 and ω = 10−4 (blue),
where M ≈ 0 for ϕobs > 0.195;
and at F||ac = 0.5 and ω = 10−4 (green),
where M ≈ 0 for ϕobs > 0.155.
(b) M vs ac frequency ω
for the system in Fig. 1(a-c) at
ϕtot = 0.275, ϕobs = 0.1256, and Fac = 0.5
for transverse (pink circles) and longitudinal (blue squares) ac driving
showing a low frequency clogged state,
an intermediate frequency flowing state, and a high frequency clogged state.
The letters a, b, c mark the frequencies at which the images in Fig. 1(a-c) were
obtained.
(c) M vs F⊥ac for the system in (b)
under transverse driving with ω = 10−4 (blue),
10−3 (green), 10−2 (gold), and 10−1 (red).
(d) M vs Fac|| at the same frequencies as
in (c) under longitudinal driving.
|