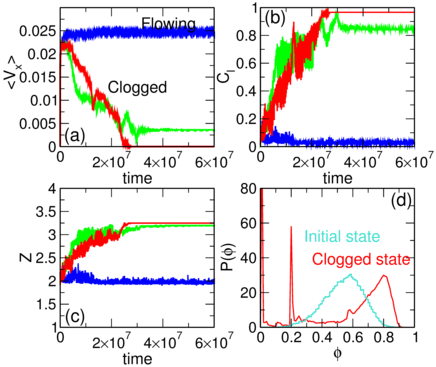
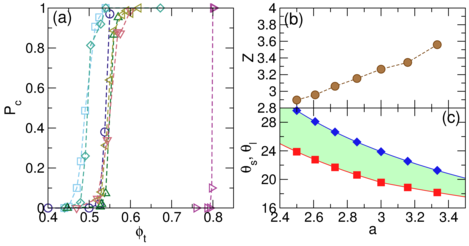
 Figure 3: (a) The clogging probability Pc vs
ϕt for varied obstacle lattice constant a=2.5 (dark blue circles),
2.609 (light blue squares), 2.727 (light green diamonds), 2.857 (dark green up triangles),
3.0 (orange left triangles), 3.158 (red down triangles), and 3.33
(magenta right triangles).
(b) The average value of Z for realizations that clog vs a
increases monotonically.
(c) Angles θs (red squares) and θl
(blue diamonds) at which x-direction channeling is lost for
the small and large disks, respectively, vs a. For driving angles falling within the
green shaded region, size-dependent clogging can occur.
Figure 3: (a) The clogging probability Pc vs
ϕt for varied obstacle lattice constant a=2.5 (dark blue circles),
2.609 (light blue squares), 2.727 (light green diamonds), 2.857 (dark green up triangles),
3.0 (orange left triangles), 3.158 (red down triangles), and 3.33
(magenta right triangles).
(b) The average value of Z for realizations that clog vs a
increases monotonically.
(c) Angles θs (red squares) and θl
(blue diamonds) at which x-direction channeling is lost for
the small and large disks, respectively, vs a. For driving angles falling within the
green shaded region, size-dependent clogging can occur.
|