Physical Review E 95, 012607 (2016)

Collective Transport for Active Matter Run-and-Tumble Disk Systems on a Traveling-Wave Substrate

Cs. Sándor1,2, A. Libál1,2, C. Reichhardt1 and C. J. Olson Reichhardt1

1Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Mathematics and Computer Science Department, Babes-Bolyai University, Cluj 400084, Romania

(Received 1 November 2016; published 17 January 2017)

We numerically examine the transport of an assembly of active run-and-tumble disks interacting with a traveling wave substrate. We show that as a function of substrate strength, wave speed, disk activity, and disk density, a variety of dynamical phases arise that are correlated with the structure and net flux of disks. We find that there is a sharp transition into a state where the disks are only partially coupled to the substrate and form a phase separated cluster state. This transition is associated with a drop in the net disk flux and can occur as a function of the substrate speed, maximum substrate force, disk run time, and disk density. Since variation of the disk activity parameters produces different disk drift rates for a fixed traveling wave speed on the substrate, the system we consider could be used as an efficient method for active matter species separation. Within the cluster phase, we find that in some regimes the motion of the cluster center of mass is in the opposite direction to that of the traveling wave, while when the maximum substrate force is increased, the cluster drifts in the direction of the traveling wave. This suggests that swarming or clustering motion can serve as a method by which an active system can collectively move against an external drift.
I. INTRODUCTION
II. SIMULATION
III. RESULTS
IV. FORWARD AND BACKWARD CLUSTER MOTION
V. SUMMARY
REFERENCES


I.  INTRODUCTION

Collections of interacting self-motile objects fall into the class of systems known as active matter [1,2], which can be biological in nature such as swimming bacteria [3] or animal herds [4], a social system such as pedestrian or traffic flow [5], or a robotic swarm [6,7]. There are also a wide range of artificial active matter systems such as self-propelled colloidal particles [8,9,10]. Studies of these systems have generally focused on the case where the motile objects interact with either a smooth or a static substrate; however, the field is now advancing to a point where it is possible to ask how such systems behave in more complex static or dynamic environments.
One subclass of active systems is a collection of interacting disks that undergo either run-and-tumble [11,12] or driven diffusive [13,14,15] motion. Such systems have been shown to exhibit a transition from a uniform density liquid state to a motility-induced phase separated state in which the disks form dense clusters surrounded by a low density gas phase [9,10,11,12,13,14,15,16,17,18]. Recently it was shown that when phase-separated run-and-tumble disks are coupled to a random pinning substrate, a transition to a uniform density liquid state occurs as a function of the maximum force exerted by the substrate [19]. In other studies of run-and-tumble disks driven over an obstacle array by a dc driving force, the onset of clustering coincides with a drop in the net disk transport since a large cluster acts like a rigid object that can only move through the obstacle array with difficulty; in addition, it was shown that the disk transport was maximized at an optimal activity level or disk running time [20]. Studies of flocking or swarming disks that obey modified Vicsek models of self-propulsion [21] interacting with obstacle arrays indicate that there is an optimal intrinsic noise level at which collective swarming occurs [22,23], and that transitions between swarming and non-swarming states can occur as a function of increasing substrate disorder [24]. The dynamics in such swarming models differ from those of the active disk systems, so it is not clear whether the same behaviors will occur across the two different systems.
A number of studies have already considered overdamped active matter such as bacteria or run-and-tumble disks interacting with periodic obstacle arrays [25] or asymmetric arrays [26,27,28,29]. Self-ratcheting behavior occurs for the asymmetric arrays when the combination of broken detailed balance and the substrate asymmetry produces directed or ratcheting motion of the active matter particles [30,31], and it is even possible to couple passive particles to the active matter particles in such arrays in order to shuttle cargo across the sample [29]. In the studies described above, the substrate is static, and external driving is introduced via fluid flow or chemotactic effects; however, it is also possible for the substrate itself to be dynamic, such as in the case of time dependent optical traps [32,33] or a traveling wave substrate. Theoretical and experimental studies of colloids or cells in traveling wave potentials reveal a rich variety of dynamical phases, self-assembly behaviors, and directed transport [34,35,36,37,38,39,40,41].
Here we examine a two-dimensional system of run and tumble active matter disks that can exhibit motility induced phase separation interacting with a periodic quasi-one dimensional (q1D) traveling wave substrate. In the low activity limit, the substrate-free system forms a uniform liquid state, while in the presence of a substrate, the disks are readily trapped by the substrate minima and swept through the system by the traveling wave. As the activity increases, a partial decoupling transition of the disks and the substrate occurs, producing a drop in the net effective transport. This transition is correlated with the onset of the phase separated state, in which the clusters act as large scale composite objects that cannot be transported as easily as individual disks by the traveling wave. We also find that the net disk transport is optimized at particular traveling wave speeds, disk run length, and substrate strength. In the phase separated state we observe an interesting effect where the center of mass of each cluster moves in the direction opposite to that in which the traveling wave is moving, and we also find reversals to states in which the clusters and the traveling wave move in the same direction. The reversed motion of the clusters arises due to asymmetric growth and shrinking rates on different sides of the cluster. The appearance of backward motion of the cluster center of mass suggests that certain biological or social active systems can move against biasing drifts by forming large collective objects or swarms.
Fig1.png
Figure 1: Schematic of the system. Red spheres represent the active run and tumble disks in a two-dimensional system interacting with a periodic q1D traveling wave potential which is moving in the positive x-direction (arrow) with a wave speed of vw.

II.  SIMULATION

We model a two-dimensional system of N run and tumble disks interacting with a q1D traveling wave periodic substrate, as shown in the schematic in Fig. 1 where the substrate moves to the right at a constant velocity vw. The dynamics of each disk is governed by the following overdamped equation of motion:
η dri
dt
 = Finteri + Fmi + Fsi ,
(1)
where the damping constant is η = 1.0. Here the net velocity of disk i produced by self-propulsion, disk-disk interaction, and substrate forces is dri/dt. The disk-disk repulsive interaction force Finteri is modeled as a harmonic spring, Finteri=∑j ≠ iNΘ(dij−2R)k(dij−2R)∧dij, where R=1.0 is the disk radius, dij=|ri−rj| is the distance between disk centers, ∧dij=(ri−rj)/dij, and the spring constant k=20.0 is large enough to prevent significant disk-disk overlap under the conditions we study yet small enough to permit a computationally efficient time step of δt=0.001 to be used. We consider a sample of size L ×L with L=300, and describe the disk density in terms of the area coverage ϕ = NπR2/L2. The run and tumble self-propulsion is modeled with a motor force Fmi of fixed magnitude Fm=1.0 that acts in a randomly chosen direction during a run time of ~tr. After this run time, the motor force instantly reorients into a new randomly chosen direction for the next run time. We take ~tr to be uniformly distributed over the range [tr,2tr], using run times ranging from tr=1 ×103 to tr=3 ×105. For convenience we describe the activity in terms of the run length rl=Fmtrδt, which is the distance a disk would move during a single run time in the absence of a substrate or other disks. The substrate is modeled as a time-dependent sinusoidal force Fsi(t)=Assin(2πxi/a−vw t) where As is the substrate strength and xi is the x position of disk i. We take a substrate periodicity of a = 15 so that the system contains 20 minima. The substrate travels at a constant velocity of vw in the positive x-direction. We measure the average drift velocity of the disks in the direction of the traveling wave, 〈V〉 = N−1∑Nivi·∧x. We vary the run length, substrate strength, disk density, and wave speed. In each case we wait for a fixed time of 5 ×106 simulation time steps before taking measurements to avoid any transient effects.
Fig2.png
Figure 2: (a) The average velocity per disk 〈V〉 vs wave speed vw for a system with N=13000 disks, ϕ = 0.45376, and rl = 300 for varied substrate strengths of As=0.5 to 3.0. The dashed line indicates the limit in which all the disks move at the wave speed, 〈V〉 = vw. (b) The corresponding number ~CL of disks that are in a cluster vs wave speed. The inset shows the regions of cluster and non-cluster (NC) states as a function of vw vs As. (c) The number ~P6 of sixfold-coordinated disks vs wave speed vw.

III.  RESULTS

In Fig. 2(a) we plot the average velocity per disk 〈V〉 versus wave speed vw at different substrate strengths As for a system containing N=13000 active disks, corresponding to ϕ = 0.45376, at rl = 300, a running length at which the substrate-free system forms a phase separated state. The number of disks that are in the largest cluster, ~CL, serves as an effective measure of whether the system is in a phase separated state or not. We measure ~CL using the cluster identification algorithm described in Ref. [42], which identifies all disks that are in force contact with a given disk, a well defined quantity. Once all force contact clusters have been identified, it is straightforward to pick out the largest cluster by simple disk counting. We call the system phase separated when ~CL/N > 0.55. In Fig. 2(b) we plot ~CL versus vw at varied As, and in Fig. 2(c) we show the corresponding number of sixfold-coordinated disks, ~P6=∑iNδ(zi−6), where zi is the coordination number of disk i determined from a Voronoi construction [43]. In phase separated states, most of the disks within a cluster have zi=6 due to the triangular ordering of the densely packed state. In Fig. 2(a), the linearly increasing dashed line denotes the limit in which all the disks move with the substrate so that 〈V〉 = vw . At As = 3.0, 〈V〉 initially increases linearly, following the dashed line, up to vw = 1.25, indicating that there is a complete locking of the disks to the substrate. For vw > 1.25, there is a slipping process in which the disks cannot keep up with the traveling wave and jump to the next well. A maximum in 〈V〉 appears near vw = 2.0, and there is a sharp drop in 〈V〉 near vw = 5.0, which also coincides with a sharp increase in ~CL and ~P6. The 〈V〉 versus vw curves for As > 1.0 all show similar trends, with a sharp drop in 〈V〉 accompanied by an increase in ~CL and ~P6, showing that the onset of clustering results in a sharp decrease in 〈V〉. For As ≤ 1.0, the substrate is weak enough that the system remains in a cluster state even at vw = 0, indicating that a transition from a cluster to a non-cluster state can also occur as a function of substrate strength. In the inset of Fig. 2(b) we show the regions in which clustering and non-clustering states appear as a function of vw versus As. At vw = 0, there is a substrate-induced transition from a cluster to a non-cluster state near As = 1.0, while for higher As, the location of the transition shifts linearly to higher vw with increasing As. Since the motor force is Fm=1.0, when As < 1.0 individual disks can escape from the substrate minima, so provided that rl is large enough, the disks can freely move throughout the entire system and form a cluster state. For As > 1.0, the disks are confined by the substrate minima, but when vw becomes large enough, the disks can readily escape the minima and again form a cluster state.
Fig3.png
Figure 3: (a) 〈V〉/vw vs As for the system in Fig. 2 at vw = 0.6. (b) The corresponding normalized CL showing that the transition from a cluster to a non-cluster state coincides with an increase in 〈V〉/vw. (c) 〈V〉/vw vs As for the same system with vw=2.0 where the cluster to non-cluster transition occurs at a higher value of As. (d) The corresponding normalized CL vs As.
Fig4.png
Figure 4: The real space positions of the active disks for the system in Fig. 3(a,b) with vw = 0.6. (a) At As = 0.75, a phase separated state appears. (b) At As = 2.5, the disks are strongly localized in the substrate minima and move with the substrate.
To highlight the correlation between the changes in the transport and the onset of clustering, in Fig. 3(a,b) we plot 〈V〉/vw and the normalized CL=~CL/N versus As at a fixed value of vw = 0.6 from the system in Fig. 2. Here the cluster to non-cluster transition occurs at As = 1.25, as indicated by the drop in CL which also coincides with a jump in 〈V〉/vw. For this value of vw, a complete locking between the disks and the traveling wave occurs for As ≥ 3.0, where 〈V〉/vw = 1.0. In Fig. 3(c,d) we plot 〈V〉/vw and CL versus As for the same system at vw = 2.0, where the cluster to non-cluster transition occurs at a higher value of As = 2.0. This transition again coincides with a sharp increase in 〈V〉/vw. In Fig. 4(a) we show images of the disk configurations for the system in Fig. 3(a,b) with vw=0.6 at As = 0.75, where the disks form a cluster state, while in Fig. 4(b), at As=2.5 in the same system, the clustering is lost and the disks are strongly trapped in the substrate minima, forming chain like states that move with the substrate. These results indicate that the clusters act as composite objects that only weakly couple to the substrate.
Fig5.png
Figure 5: (a) 〈V〉 vs rl in samples with As = 2.0 and ϕ = 0.453 for varied vw from vw=0.25 to vw=6.0. (b) The corresponding ~CL vs rl.
Fig6.png
Figure 6: A sample with As=2.0 and ϕ = 0.453 for rl = 5 (red squares) and rl=200 (blue circles). (a) 〈V〉 vs vw. (b) CL vs vw.
We next examine the case with a fixed substrate strength of As = 2.0 and varied rl. Figure 5(a) shows 〈V〉 versus rl for vw values ranging from vw=0.25 to vw=6.0, and Fig. 5(b) shows the corresponding ~CL versus rl. For vw < 3.0 the system remains in a non-cluster state for all values of rl, while for vw ≥ 3.0 there is a transition from a non-cluster to a cluster state with increasing rl as indicated by the simultaneous drop in 〈V〉 and increase in ~CL. In Fig. 6(a,b) we plot 〈V〉 and CL versus vw at As = 2.0 for rl = 200 and rl=5.0. The system is in a non-cluster state for all vw when rl = 5.0, and there is a peak in 〈V〉 near vw = 1.0, while for rl = 200 there is a transition to a cluster state close to vl = 3.0 which coincides with a drop in 〈V〉 that is much sharper than the decrease in 〈V〉 with increasing vw for the rl = 5 system. In general, when rl is small, the net transport of disks through the sample is greater than in samples with larger rl. The fact that the net disk transport varies with varying rl suggests that traveling wave substrates could be used as a method for separating different types of active matter, such as clustering and non-clustering species.
Fig7.png
Figure 7: (a) 〈V〉 vs vw at ϕ = 0.56 and rl = 300 for varied As = 0.5 to As=4.0. (b) The corresponding ~CL vs vw. (c) 〈V〉 vs ϕ for As = 2.5, rl = 300 and vw = 2.0. (d) The corresponding ~Cl (blue circles) and ~P6 (red squares) vs ϕ where the onset of clustering occurs near ϕ = 0.6 at the same point for which there is a drop in 〈V〉 in panel (c).
When we vary the disk density ϕ while holding rl fixed, we find results similar to those described above. In Fig. 7(a) we plot 〈V〉 versus vw at ϕ = 0.56 for varied As from As=0.5 to As=4.0, where we find a similar trend in which 〈V〉 increases with increasing wave speed when the disks are strongly coupled to the substrate. A transition to a cluster state occurs at higher vw as shown in Fig. 7(b) where we plot ~CL versus vw for the same samples. The increase in ~CL at the cluster state onset coincides with a drop in 〈V〉. In Fig. 7(c) we plot 〈V〉 versus ϕ for a system with fixed vw = 2.0, As = 2.5, and rl = 300, while in Fig. 7(d) we show the corresponding ~CL and ~P6 versus ϕ. A transition from the non-cluster to the cluster state occurs near ϕ = 0.6, which correlates with a sharp drop in 〈V〉 and a corresponding increase in ~CL and ~P6.
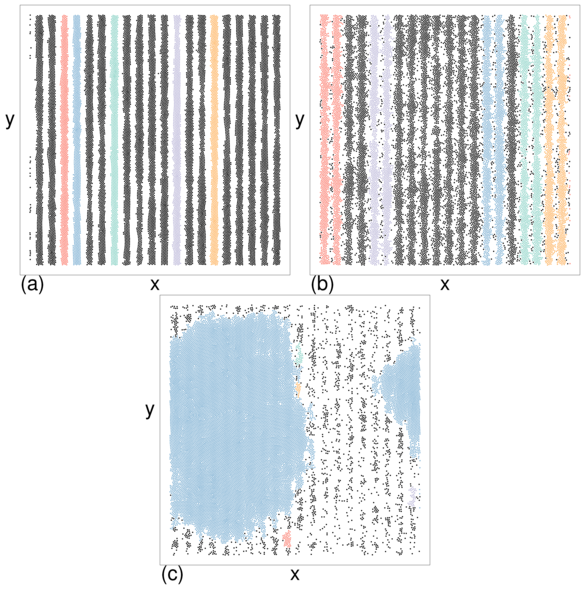
Fig8.png
Figure 8: The disk positions on the traveling wave substrate for the system in Fig. 7(a) at ϕ = 0.56. Colors indicate disks belonging to the five largest clusters. (a) Complete locking at As = 4.0 and vw = 1.0, where the transport efficiency is 〈V〉/vw = 0.998. (b) Partial locking at As = 2.0 and vw = 1.5, where 〈V〉/vw = 0.41. (c) Weak locking at As = 1.0 and vw = 0.6 with 〈V〉/vw = 0.078.
In Fig. 8(a) we show the disk configurations from the system in Fig. 7(a) at As = 4.0 and vw = 1.0. Here 〈V〉/vw = 0.998, indicating that the disks are almost completely locked with the traveling wave motion and there is little to no slipping of the disks out of the substrate minima. In Fig. 8(b), the same system at As = 2.0 and vw = 1.5 has a transport efficiency of 〈V〉/vw = 0.41. No clustering occurs but there are numerous disks that slip as the traveling wave moves. At As = 1.0 and vw = 0.6 in Fig. 8(c) there is a low transport efficiency of 〈V〉/vw=0.078. The system forms a cluster state and smaller numbers of individual disks outside of the cluster are transported by the traveling wave.

IV.  FORWARD AND BACKWARD CLUSTER MOTION

Fig9.png
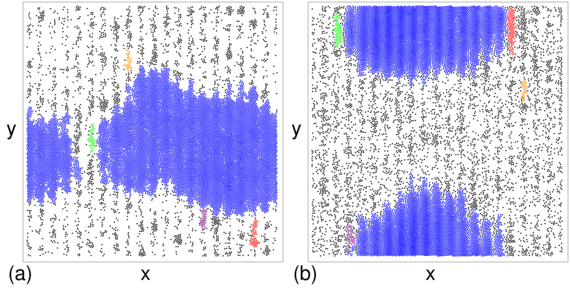
Figure 9: The center of mass XCOM location of a cluster vs time in simulation time steps for a system with ϕ = 0.454 and rl = 300. (a) At As = 1.25 and vw = 0.6, the cluster moves in the negative x-direction, against the direction of the traveling wave. (b) At As = 0.5 and vw = 4.0, the cluster is stationary. (c) At As = 3.0 and vw = 7.0, the cluster moves in the positive x-direction, with the traveling wave. The dip indicates the point at which the center of mass passes through the periodic boundary conditions.
In general, we find that when the traveling wave is moving in the positive x-direction, 〈V〉 > 0; however, within the cluster phase, the center of mass motion of a cluster can be in the positive or negative x direction or the cluster can be almost stationary. By using the cluster algorithm to identify the location of the cluster center of mass, we can track the x-direction motion of the cluster center of mass XCOM over fixed time periods, as shown in Fig. 9(a) for a system with ϕ = 0.454, rl = 300, As = 1.25, and vw = 0.6. During the course of 6×106 simulation time steps the cluster moves in the negative x-direction a distance of 235 units, corresponding to a space containing 16 potential minima. Even though the net disk flow is in the positive x direction, the cluster itself drifts in the negative x direction. In Fig. 9(b) at As = 0.5 and vw = 4.0, the disks are weakly coupled to the substrate and the cluster is almost completely stationary. Figure 9(c) shows that at As = 3.0 and vw = 7.0, the cluster center of mass motion is now in the positive x direction, and the cluster translates a distance equal to almost 20 substrate minima during the time period shown. The apparent dip in the center of mass motion is due to the periodic boundary conditions.
Fig10.png
Figure 10: Height field of the direction and magnitude of the center of mass motion in the x direction, VCOM, as a function of As vs vw for the cluster obtained after 4×106 simulation steps. The gray area indicates a regime in which there is no cluster formation.
Fig11.png
Figure 11: The disk positions for the system in Figs. 9 and  10. (a) At As = 1.0 and vw = 0.4, the cluster drifts in the negative x-direction. (b) At As = 3.0 and vw = 5.0, the cluster drifts in the positive x-direction.
We have conduced a series of simulations and measured the direction and amplitude VCOM = d XCOM/dt of the center of mass motion, as plotted in Fig. 10 as a function of As versus wave speed for the system in Fig. 7. The gray area indicates a region in which clusters do not occur, and in general we find that the negative cluster motion occurs at lower wave speeds while the positive motion occurs for stronger substrates and higher wave speeds. There are two mechanisms that control the cluster center of mass motion. The first is the motion of the substrate itself, which drags the cluster in the positive x direction, and the second is the manner in which the cluster grows or shrinks on its positive x and negative x sides. At lower substrate strengths and low wave speeds, the disks in the cluster are weakly coupled to the substrate so the cluster does not move with the substrate. In this case the disks can leave or join the cluster anywhere around its edge; however, disks tend to join the cluster at a higher rate on its negative x side since individual disks, driven by the moving substrate, collide with the negative x side of the cluster and can become trapped in this higher density area. The positive x side of the cluster tends to shed disks at a higher rate since the disks can be carried away by the moving substrate into the low density gas region. The resulting asymmetric growth rate causes the cluster to drift in the negative x direction. There is a net overall transport of disks in the positive x direction due to the large number of gas phase disks outside of the cluster region which follow the motion of the substrate. Figure 11(a) shows the disk positions at As = 1.0 and vw = 0.4, where the cluster is drifting in the negative x direction. For strong substrate strengths, all the disks that are outside of the cluster become strongly confined in the q1D substrate minima, and the disk density inside the cluster itself starts to become modulated by the substrate. Under these conditions, the cluster is dragged along with the traveling substrate in the positive x direction, as illustrated in Fig. 11(b) for As = 3.0 and vw = 5.0. These results suggest that it may be possible for certain active matter systems to collectively form a cluster state in order to move against an external bias even when isolated individual particles on average move with the bias.

V.  SUMMARY

We have examined run and tumble active matter disks interacting with traveling wave periodic substrates. We find that in the non-phase separated state, the disks couple to the traveling waves, and that at the transition to the cluster state, there is a partial decoupling from the substrate and the net transport of disks by the traveling wave is strongly reduced. We also find a transition from a cluster state to a periodic quasi-1D liquid state for increasing substrate strength, as well as a transition back to a cluster state for increasing traveling wave speed. We show that there is a transition from a non-cluster to a cluster state as a function of increasing disk density which is correlated with a drop in the net disk transport. Since disks with different run times drift with different velocities, our results indicate that traveling wave substrates could be an effective method for separating active matter particles with different mobilities. Within the regime in which the system forms a cluster state, we find that as a function of wave speed and substrate strength, there are weak substrate regimes where the center of mass of the cluster moves in the opposite direction from that of the traveling wave, while for stronger substrates, the cluster center of mass moves in the same direction as the traveling wave. The reversed cluster motion occurs due to the spatial asymmetry of the rate at which disks leave or join the cluster. This suggests that collective clustering could be an effective method for forming an emergent object that can move against gradients or drifts even when individual disks on average move with the drift.
This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

  REFERENCES

[1]
M.C. Marchetti, J.F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, and R.A. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys. 85, 1143 (2013).
[2]
C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, Active Brownian particles in complex and crowded environments, Rev. Mod. Phys. 88, 045006 (2016).
[3]
H. C. Berg, Random Walks in Biology (Princeton University Press, Princeton, 1983).
[4]
C. Castellano, S. Fortunato, and V. Loreto, Statistical physics of social dynamics, Rev. Mod. Phys. 81, 591 (2009).
[5]
D. Helbing, Traffic and related self-driven many-particle systems, Rev. Mod. Phys. 73, 1067 (2001).
[6]
M. Rubenstein, A. Cornejo, and R. Nagpal, Programmable self-assembly in a thousand-robot swarm, Science 345, 795 (2014).
[7]
M. Mijalkov, A. McDaniel, J. Wehr, and G. Volpe, Engineering sensorial delay to control phototaxis and emergent collective behaviors, Phys. Rev. X 6, 011008 (2016).
[8]
J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh, and R. Golestanian, Self-motile colloidal particles: From directed propulsion to random walk, Phys. Rev. Lett. 99, 048102 (2007).
[9]
J. Palacci, S. Sacanna, A.P. Steinberg, D.J. Pine, and P.M. Chaikin, Living crystals of light-activated colloidal surfers, Science 339, 936 (2013).
[10]
I. Buttinoni, J. Bialk' e, F. Kümmel, H. Löwen, C. Bechinger, and T. Speck, Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles, Phys. Rev. Lett. 110, 238301 (2013).
[11]
A.G. Thompson, J. Tailleur, M. E. Cates, and R. A. Blythe, Lattice models of nonequilibrium bacterial dynamics, J. Stat. Mech. 2011, P02029 (2011).
[12]
C. Reichhardt and C. J. Olson Reichhardt, Active microrheology in active matter systems: Mobility, intermittency, and avalanches, Phys. Rev. E 91, 032313 (2015).
[13]
Y. Fily and M.C. Marchetti, Athermal phase separation of self-propelled particles with no alignment, Phys. Rev. Lett. 108, 235702 (2012).
[14]
G.S. Redner, M.F. Hagan, and A. Baskaran, Structure and dynamics of a phase-separating active colloidal fluid, Phys. Rev. Lett. 110, 055701 (2013).
[15]
M. E. Cates and J. Tailleur, When are active Brownian particles and run-and-tumble particles equivalent? Consequences for motility-induced phase separation, Europhys. Lett. 101, 20010 (2013).
[16]
B. M. Mognetti, A. Saric, S. Angioletti-Uberti, A. Cacciuto, C. Valeriani, and D. Frenkel, Living clusters and crystals from low-density suspensions of active colloids, Phys. Rev. Lett. 111, 245702 (2013).
[17]
D. Levis and L. Berthier, Clustering and heterogeneous dynamics in a kinetic Monte Carlo model of self-propelled hard disks, Phys. Rev. E 89, 062301 (2014).
[18]
M.E. Cates and J. Tailleur, Motility-induced phase separation, Ann. Rev. Condens. Matt. Phys. 6, 219 (2015).
[19]
Cs. Sándor, A. Libál, C. Reichhardt, and C.J. Olson Reichhardt, Dewetting and spreading transitions for active matter on random pinning substrates, J. Chem. Phys. 146, 204903 (2017).
[20]
C. Reichhardt and C. J. Olson Reichhardt, Active matter transport and jamming on disordered landscapes, Phys. Rev. E 90, 012701 (2014).
[21]
T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, Novel type of phase transition in a system of self-driven particles, Phys. Rev. Lett. 75, 1226 (1995).
[22]
O. Chepizhko, E.G. Altmann, and F. Peruani, Optimal noise maximizes collective motion in heterogeneous media, Phys. Rev. Lett. 110, 238101 (2013).
[23]
O. Chepizhko and F. Peruani, Active particles in heterogeneous media display new physics, Eur. Phys. J. Spec. Top. 224, 1287 (2015).
[24]
D. Quint and A. Gopinathan, Topologically induced swarming phase transition on a 2D percolated lattice, Phys. Biol. 12, 046008 (2015).
[25]
G. Volpe, I. Buttinoni, D. Vogt, H.J. Kümmerer, and C. Bechinger, Microswimmers in patterned environments, Soft Matter 7, 8810 (2011).
[26]
P. Galajda, J. Keymer, P. Chaikin, and R. Austin, A wall of funnels concentrates swimming bacteria, J. Bacteriol. 189, 8704 (2007).
[27]
M.B. Wan, C.J. Olson Reichhardt, Z. Nussinov, and C. Reichhardt, Rectification of swimming bacteria and self-driven particle systems by arrays of asymmetric barriers, Phys. Rev. Lett. 101, 018102 (2008).
[28]
F.Q. Potiguar, G.A. Farias, and W.P. Ferreira, Self-propelled particle transport in regular arrays of rigid asymmetric obstacles, Phys. Rev. E 90, 012307 (2014).
[29]
N. Koumakis, A. Lepore, C. Maggi, and R. Di Leonardo, Targeted delivery of colloids by swimming bacteria, Nature Commun. 4, 2588 (2013).
[30]
J. Tailleur and M. E. Cates, Sedimentation, trapping, and rectification of dilute bacteria, Europhys. Lett. 86, 60002 (2009).
[31]
C.J. Olson Reichhardt and C. Reichhardt, Ratchet effects in active matter systems, Ann. Rev. Condens. Mat. Phys. 8, 51 (2017).
[32]
S.-H. Lee, K. Ladavac, M. Polin, and D.G. Grier, Observation of flux reversal in a symmetric optical thermal ratchet, Phys. Rev. Lett. 94, 110601 (2005).
[33]
V. Blickle, T. Speck, L. Helden, U. Seifert, and C. Bechinger, Thermodynamics of a colloidal particle in a time-dependent nonharmonic potential, Phys. Rev. Lett. 96, 070603 (2006).
[34]
M. Rex, H. Löwen, and C.N. Likos, Soft colloids driven and sheared by traveling wave fields, Phys. Rev. E 72, 021404 (2005).
[35]
B.B. Yellen, R.M. Erb, H.S. Son, R. Hewlin, H. Shang, and G.U. Lee, Traveling wave magnetophoresis for high resolution chip based separations, Lab Chip. 7, 1681 (2007).
[36]
B.B. Yellen and L.N. Virgin, Nonlinear dynamics of superparamagnetic beads in a traveling magnetic-field wave, Phys. Rev. E 80, 011402 (2009).
[37]
R. Chatterjee, S. Chatterjee, P. Pradhan, and S.S. Manna, Interacting particles in a periodically moving potential: Traveling wave and transport, Phys. Rev. E 89, 022138 (2014).
[38]
A.V. Straube and P. Tierno, Tunable interactions between paramagnetic colloidal particles driven in a modulated ratchet potential, Soft Matter 10, 3915 (2014).
[39]
F. Martinez-Pedrero, P. Tierno, T.H. Johansen, and A.V. Straube, Regulating wave front dynamics from the strongly discrete to the continuum limit in magnetically driven colloidal systems, Sci. Rep. 6, 19932 (2016).
[40]
P. Tierno and A. Straube, Transport and selective chaining of bidisperse particles in a travelling wave potential, Eur. Phys. J. E 39, 54 (2016).
[41]
R.E. Goldstein, Traveling-wave chemotaxis, Phys. Rev. Lett. 77, 775 (1996).
[42]
S. Luding and H.J. Herrmann, Cluster-growth in freely cooling granular media, Chaos 9, 673 (1999).
[43]
CGAL library, http://www.cgal.org


File translated from TEX by TTHgold, version 4.00.
 Back to Home