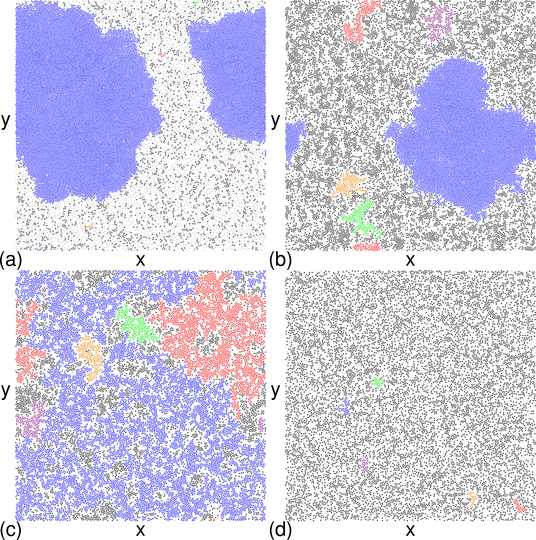
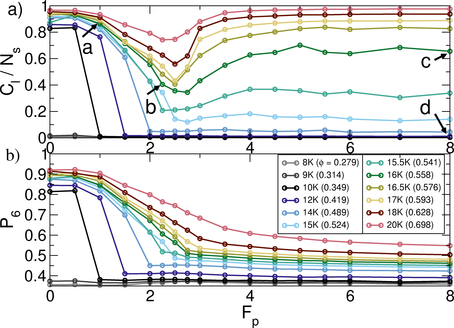
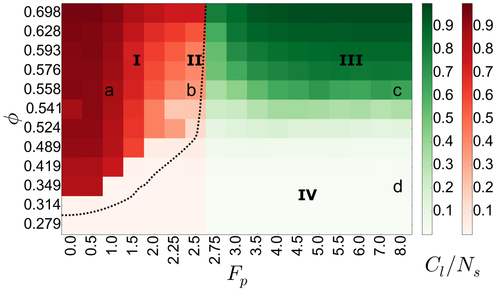
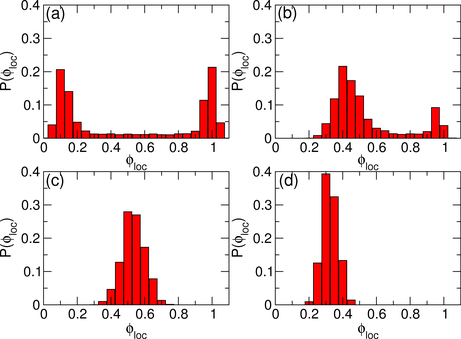
Figure 7:
The mean square displacement ∆r2 vs
time in simulation time steps
from the system in Fig. 5 at ϕ = 0.55.
(a) For lr = 1 at Fp = 0 (purple) and Fp=1.0 (dark blue),
we can fit
δr2 ∝ tα. At long times,
α = 1.0 for Fp = 0 (blue dashed line), consistent with diffusive motion,
while for Fp=1.0 we find subdiffusive behavior
with α = 0.7 (green dashed line) due to the particle trapping.
(b) ∆r2 vs time for lr = 300
at Fp = 1.0 (blue), 1.5 (green), 4.0 (orange), and 6.0 (red).
For Fp = 1.0 and Fp=1.5, in
phase I and phase II the system is superdiffusive
at short and intermediate times
with α = 1.7 (blue dashed line)
and diffusive or slightly subdiffusive at long times with α = 0.85
(purple dashed line).
For Fp = 4.0 and Fp=5.0,
the crossover to subdiffusion occurs at earlier times in phase III.
Figure 7:
The mean square displacement ∆r2 vs
time in simulation time steps
from the system in Fig. 5 at ϕ = 0.55.
(a) For lr = 1 at Fp = 0 (purple) and Fp=1.0 (dark blue),
we can fit
δr2 ∝ tα. At long times,
α = 1.0 for Fp = 0 (blue dashed line), consistent with diffusive motion,
while for Fp=1.0 we find subdiffusive behavior
with α = 0.7 (green dashed line) due to the particle trapping.
(b) ∆r2 vs time for lr = 300
at Fp = 1.0 (blue), 1.5 (green), 4.0 (orange), and 6.0 (red).
For Fp = 1.0 and Fp=1.5, in
phase I and phase II the system is superdiffusive
at short and intermediate times
with α = 1.7 (blue dashed line)
and diffusive or slightly subdiffusive at long times with α = 0.85
(purple dashed line).
For Fp = 4.0 and Fp=5.0,
the crossover to subdiffusion occurs at earlier times in phase III.
|