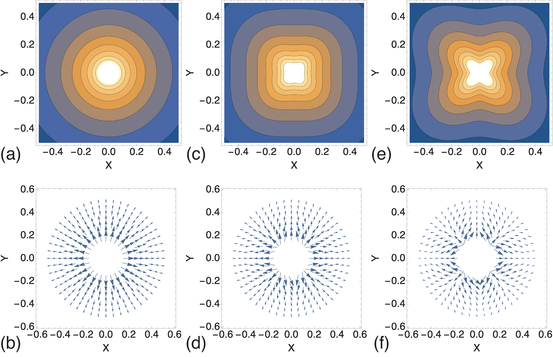
 Figure 3:
Real space VL configurations (a,c,e) and corresponding heightfield plots of the structure factor |S(k)| (b,d,f) after annealing in samples with Av = 2.0.
(a,b) The isotropic system with Aa = 0 has triangular ordering and a lattice angle θl (marked in white) of θl ≈ 60°.
(c,d) At Aa = 0.039, the vortices form a rhombic lattice with θl ≈ 76°.
(e,f) At Aa = 0.099, the vortices form a square lattice with θl=90°.
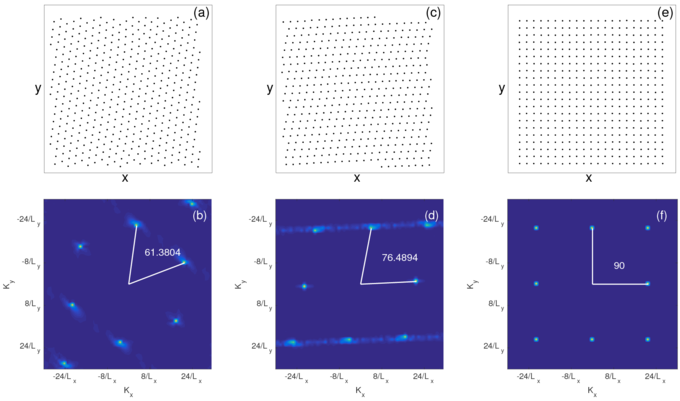
Figure 3:
Real space VL configurations (a,c,e) and corresponding heightfield plots of the structure factor |S(k)| (b,d,f) after annealing in samples with Av = 2.0.
(a,b) The isotropic system with Aa = 0 has triangular ordering and a lattice angle θl (marked in white) of θl ≈ 60°.
(c,d) At Aa = 0.039, the vortices form a rhombic lattice with θl ≈ 76°.
(e,f) At Aa = 0.099, the vortices form a square lattice with θl=90°.
|