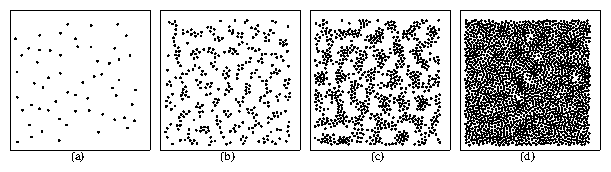
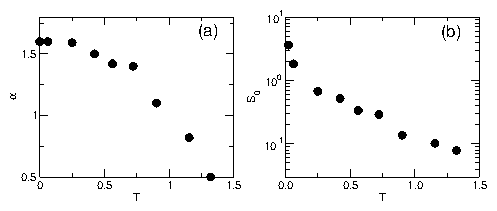
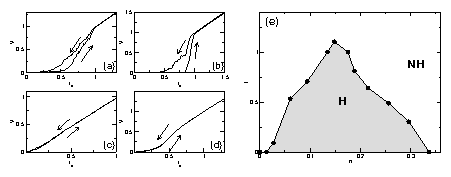
 Figure 2:
The velocity V vs driving force fd curves for
(a) density n = 0.15, T = 0.1;
(b) n = 0.06, T = 0.1;
(c) n = 0.15, T = 1.3;
(d) n = 0.34, T=0.1.
(e) Temperature T vs density n. The shaded region
indicates where hysteresis (H) is present
in the velocity-force curve. The nonhysteretic region is indicated by NH.
Figure 2:
The velocity V vs driving force fd curves for
(a) density n = 0.15, T = 0.1;
(b) n = 0.06, T = 0.1;
(c) n = 0.15, T = 1.3;
(d) n = 0.34, T=0.1.
(e) Temperature T vs density n. The shaded region
indicates where hysteresis (H) is present
in the velocity-force curve. The nonhysteretic region is indicated by NH.
|