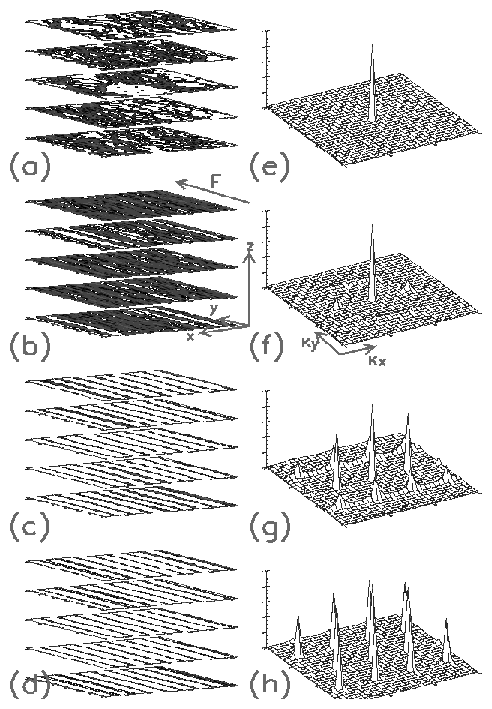
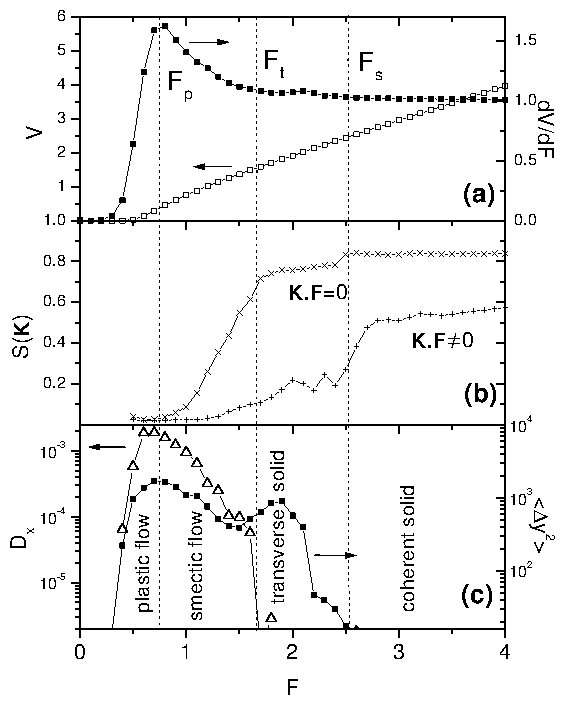
 Figure 2: (a) Velocity-force curve,
left scale, black
points, dV/dF (differential resistance), right scale, white points. (b)
Intensity of the Bragg peaks. For smectic ordering S(G1), Ky=0, (×)
symbols. For longitudinal ordering S(G2,3), Ky ≠ 0, (+) symbols.
(c) Diffusion coefficient for transverse motion Dx, (up triangles),
left scale. Longitudinal displacements
〈[∆y(t)]2〉 for a given t as a function of F,
(squares), right scale.
Figure 2: (a) Velocity-force curve,
left scale, black
points, dV/dF (differential resistance), right scale, white points. (b)
Intensity of the Bragg peaks. For smectic ordering S(G1), Ky=0, (×)
symbols. For longitudinal ordering S(G2,3), Ky ≠ 0, (+) symbols.
(c) Diffusion coefficient for transverse motion Dx, (up triangles),
left scale. Longitudinal displacements
〈[∆y(t)]2〉 for a given t as a function of F,
(squares), right scale.
|