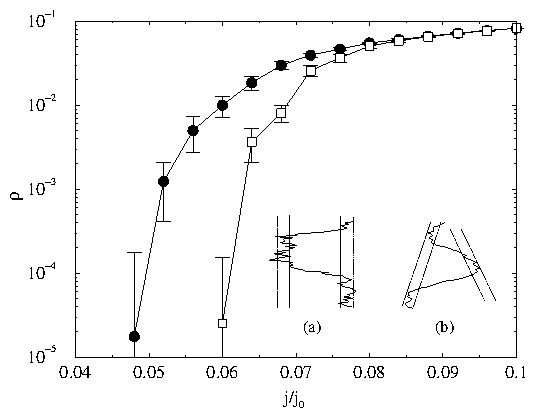
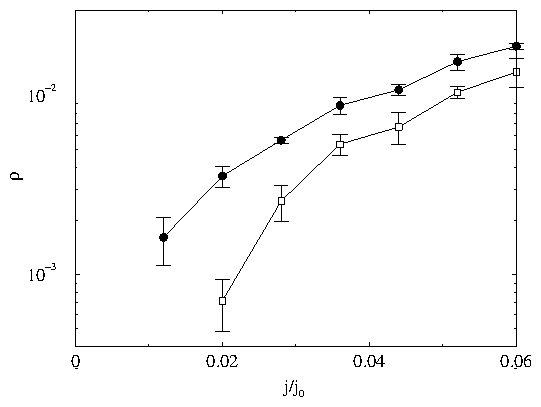
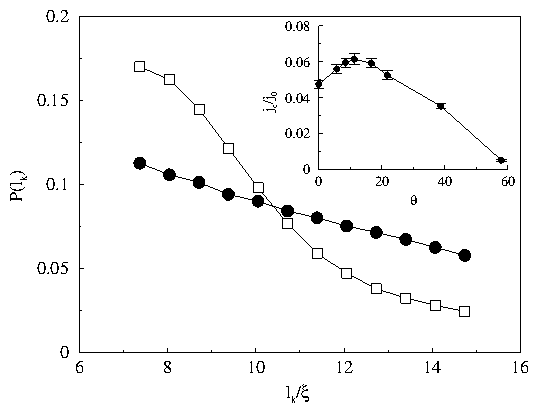
 Figure 2: Distribution of the lengths of vortex segments between kinks,
P(lk), for samples with columnar (filled circles) and splayed
(open squares) pinning, with the same parameters shown in Fig. 1
at j/j0 = 0.065 (in the vortex creep regime).
For the columnar pinning, P(lk) depends weakly on length,
but P(lk) for splayed pinning falls off more rapidly,
indicating that the kink energy
grows with length lk.
Inset:
Critical current jc
as a function of the angle ±θ
between the z axis and the splayed pins
for the system of Fig. 1.
The initial increase of jc with θ stops above
θ ∼ 10°
when the pins become so tilted that the vortices no longer accommodate
to them.
Figure 2: Distribution of the lengths of vortex segments between kinks,
P(lk), for samples with columnar (filled circles) and splayed
(open squares) pinning, with the same parameters shown in Fig. 1
at j/j0 = 0.065 (in the vortex creep regime).
For the columnar pinning, P(lk) depends weakly on length,
but P(lk) for splayed pinning falls off more rapidly,
indicating that the kink energy
grows with length lk.
Inset:
Critical current jc
as a function of the angle ±θ
between the z axis and the splayed pins
for the system of Fig. 1.
The initial increase of jc with θ stops above
θ ∼ 10°
when the pins become so tilted that the vortices no longer accommodate
to them.
|