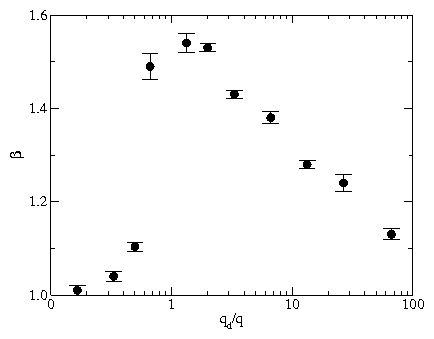
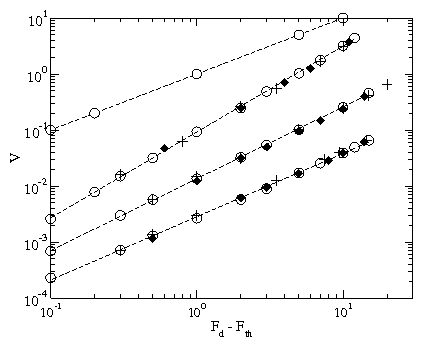
 Figure 2:
Velocity V vs applied force Fd − Fth, where Fth is the
threshold force for motion. From top to bottom, qd/q = 0.25,
1.33, 13, and 67. Dotted lines: Fits with, from top to bottom,
β = 1.0, 1.54, 1.28, and 1.13. System
sizes: L = 24 (open circles), 36 (plus signs), and 48 (filled
diamonds).
Figure 2:
Velocity V vs applied force Fd − Fth, where Fth is the
threshold force for motion. From top to bottom, qd/q = 0.25,
1.33, 13, and 67. Dotted lines: Fits with, from top to bottom,
β = 1.0, 1.54, 1.28, and 1.13. System
sizes: L = 24 (open circles), 36 (plus signs), and 48 (filled
diamonds).
|