 Figure 1:
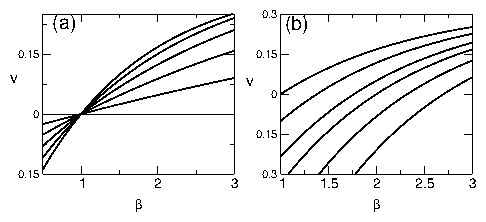
(a) Velocity v vs power-law exponent β from Eq. 2 for f1 = 1.0.
Ratcheting in the positive direction (v > 0) occurs for
β > 1. From top left to bottom left,
f2/f1 = 1.0 (flat line), 0.9, 0.8, 0.7, 0.6,
and 0.5. (b) v vs β for fixed f1/f2 = 0.5 and,
from bottom to top, τ2/τ1 = 3.25, 2.5, 2, 1.5, 1.25, and 1.
Figure 1:
(a) Velocity v vs power-law exponent β from Eq. 2 for f1 = 1.0.
Ratcheting in the positive direction (v > 0) occurs for
β > 1. From top left to bottom left,
f2/f1 = 1.0 (flat line), 0.9, 0.8, 0.7, 0.6,
and 0.5. (b) v vs β for fixed f1/f2 = 0.5 and,
from bottom to top, τ2/τ1 = 3.25, 2.5, 2, 1.5, 1.25, and 1.
|