 Figure 3:
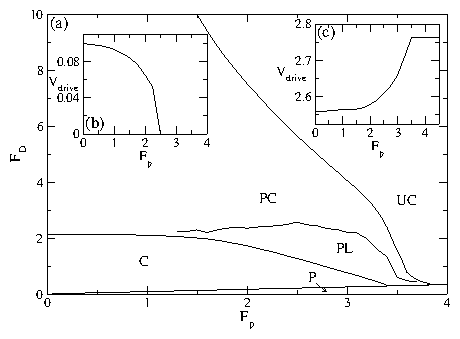
(a) The dynamic phase diagram of FD vs Fp for the system in
fig. 2 for pinning in only the drag channel.
Each region is marked: pinned (P), coupled (C),
pulse locked (PL),
partially coupled (PC), and uncoupled (UC).
(b) Vdrive versus Fp from the system in (a)
at FD = 0.2. The increasing
effective damping η*=FD/Vdrive
produces a monotonic decrease in Vdrive with increasing
Fp until the particles in the driven channel repin and the velocity
drops to zero in region P.
(c) Vdrive vs Fp
for the system in (a) at FD = 3.0.
Here Vdrive
increases with increasing Fp
until the onset of the UC phase, above which Vdrive saturates to
a constant value.
Figure 3:
(a) The dynamic phase diagram of FD vs Fp for the system in
fig. 2 for pinning in only the drag channel.
Each region is marked: pinned (P), coupled (C),
pulse locked (PL),
partially coupled (PC), and uncoupled (UC).
(b) Vdrive versus Fp from the system in (a)
at FD = 0.2. The increasing
effective damping η*=FD/Vdrive
produces a monotonic decrease in Vdrive with increasing
Fp until the particles in the driven channel repin and the velocity
drops to zero in region P.
(c) Vdrive vs Fp
for the system in (a) at FD = 3.0.
Here Vdrive
increases with increasing Fp
until the onset of the UC phase, above which Vdrive saturates to
a constant value.
|