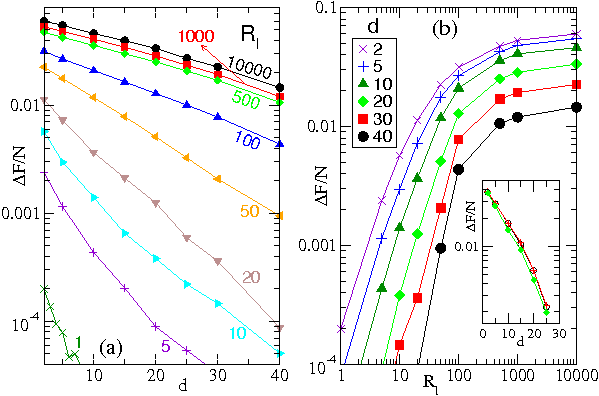
 Figure 2:
(a) ∆F/N, the attractive force between the walls, vs
d, the inter-wall distance, from ED simulations with
l=20, for various Rl, showing an exponential behavior.
(b) ∆F/N vs Rl for the same system at
various d.
For large Rl, ∆F/N saturates.
Inset: ∆F/N vs d for l=20,
Rl=40,
and N=400 in
ED simulations
(•) and MD simulations without (+) and with (⧫)
steric particle-particle interactions.
Figure 2:
(a) ∆F/N, the attractive force between the walls, vs
d, the inter-wall distance, from ED simulations with
l=20, for various Rl, showing an exponential behavior.
(b) ∆F/N vs Rl for the same system at
various d.
For large Rl, ∆F/N saturates.
Inset: ∆F/N vs d for l=20,
Rl=40,
and N=400 in
ED simulations
(•) and MD simulations without (+) and with (⧫)
steric particle-particle interactions.
|